Computation of Volume from Graphs, Arc Length, Average Value

volume of cylindrical shells formula

x = radius

f(x) = height

the above ONLY apply for functions revolving around the normal axes and not functions revolving around other vertical/horizontal lines

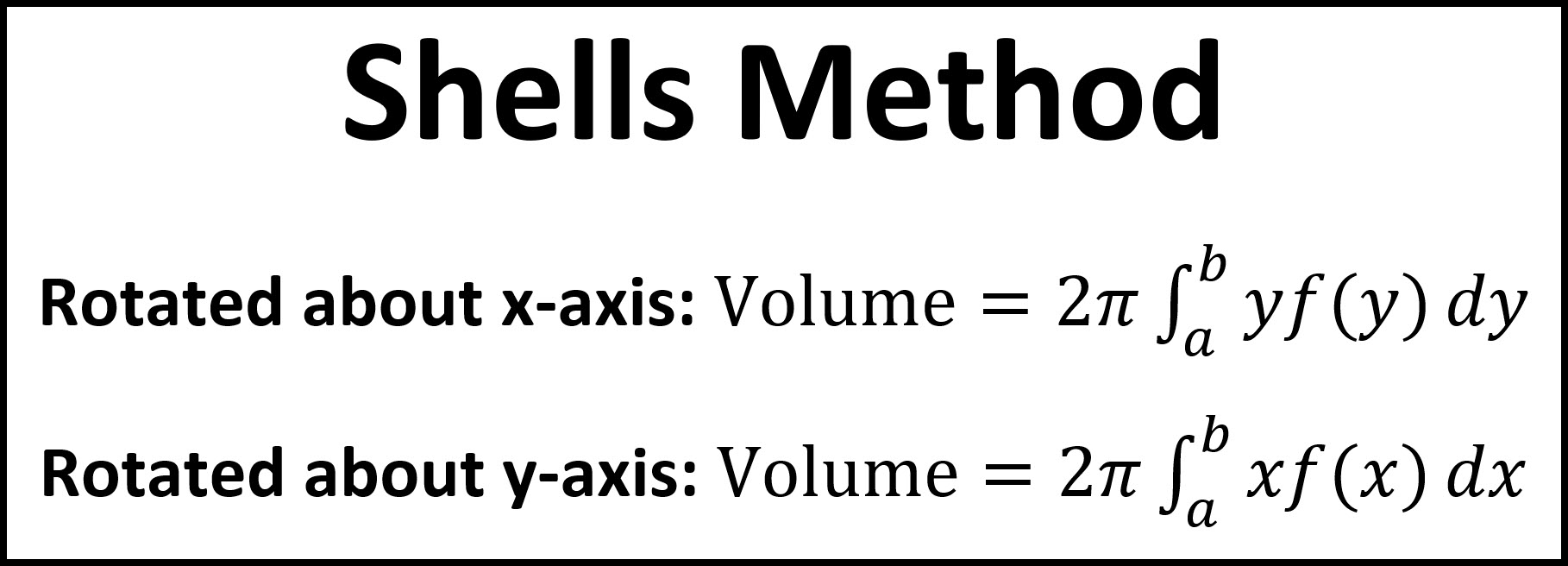
if the cross section of the volume is parallel to the y-axis, integrate with respect to ___

if the cross section of the V is || to the x-axis, integrate w.r.t ____

x; y

volume using disc method

• method is for solids WITHOUT a hollow center

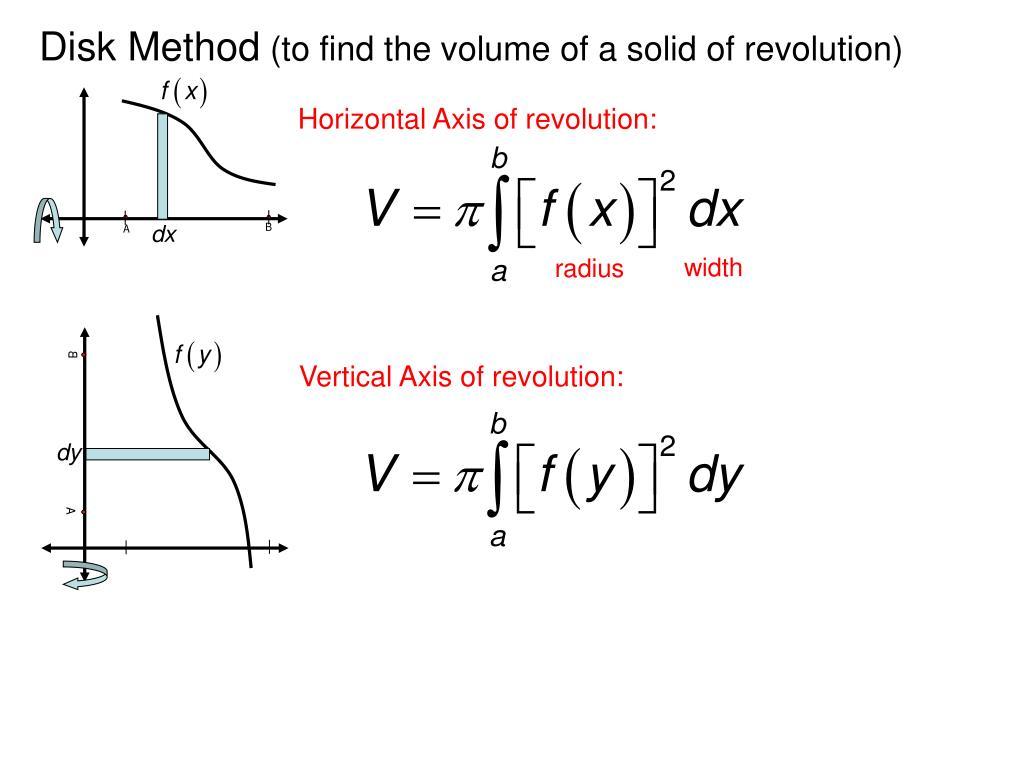
volume using washer method

• method is for solids with a hollow center

• washer method is for TWO functions that bound some area that rotates around some axis

• “outer” circle function minus “inner” circle function

work =

force/”weight” x distance, aka the integral of the force function w.r.t distance

in terms of integration, work =

the definite integral of the force function moved from position a to position b [a,b] (meaning b is the upper bound, a is the lower bound)

force function for springs

F(x) = kx for some spring constant k

• x denotes the DISPLACEMENT, the difference between initial position of the string and the final position)

• the higher displacement = upper nound and the lower displacement = lower bound

• take note of the NATURAL POSITION OF THE STRING

unit for work

Joule = kg * m²/s²

method of cylindrical shells w two functions

height (h) = f(x) - g(x)

where f(x) is the higher fn and g(x) is the lower function → FIND POINTS OF INTERSECTION

method of cylindrical shells: offset axis

if the axis is x = a where a is not 0:

if a is neg, then radius = a + x

if a is pos, then radius = a - x

average value

for interval [a,b]

mean value thm

if f(x) is continuous on [a,b], then there is a number c in that interval where:

f( c ) = average f num

arc length of f(x) on interval [a,b] formula

dy/dx = f’(x)

• aim for a squared factor format

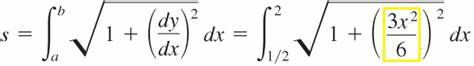
comparison Thm

a known convergent >= improper integral >= 0

• if the above equality holds true, then the improper integral is also convergent

• improper integral >= a known divergent >= 0

• If the above equality is met, then the imp integral is also divergent

• YOU MUST SHOW THAT ALL FNS CAN ONLY YIELD POS VALUES FOR THE GIVEN INTERVAL [a,b] (where one of the bounds is positive)

a known convergent 1/x^p

if p > 1, 1/x^p is convergent