Chapter 2: Reasoning and Proofs Overview

Conditional statement

A logical statement that has a hypothesis and a conclusion.

If-then form

A conditional statement in the form 'if p, then q'.

Hypothesis

The 'if' part of a conditional statement written in if-then form.

Conclusion

The 'then' part of a conditional statement written in if-then form.

Negation

The opposite of a statement.

Converse

The statement formed by exchanging the hypothesis and conclusion of a conditional statement.

Inverse

The statement formed by negating both the hypothesis and conclusion of a conditional statement.

Contrapositive

The statement formed by negating both the hypothesis and conclusion of the converse of a conditional statement.

Two-column proofs

A type of proof that has numbered statements and corresponding reasons that show an argument in a logical order.

Equivalent statements

Two related conditional statements that are both true or both false.

Perpendicular lines

Two lines that intersect to form a right angle.

Biconditional statement

A statement that contains the phrase 'if and only if'.

Truth table

A table that shows the truth values for a hypothesis, conclusion, and conditional statement.

Conjecture

An unproven statement that is based on observations.

Inductive reasoning

A process that includes looking for patterns and making conjectures.

Counterexample

A specific case for which a conjecture is false.

Deductive reasoning

A process that uses facts, definitions, accepted properties, and laws of logic to form a logical argument.

Theorem

A statement that can be proven.

Truth value

A value that represents whether a statement is true (T) or false (F).

Line perpendicular to a plane

A line that intersects the plane in a point and is perpendicular to every line in the plane that intersects it at that point.

Proof

A logical argument that uses deductive reasoning to show that a statement is true.

Flowchart proof

A type of proof that uses boxes and arrows to show the flow of a logical argument.

Paragraph proof

A style of proof that presents statements and reasons as sentences in a paragraph, using words to explain the logical flow of an argument.

Two Point Postulate

Through any two points, there exists exactly one line.

Line-Point Postulate

A line contains at least two points.

Line Intersection Postulate

If two lines intersect, then their intersection is exactly one point.

Three Point Postulate

Through any three noncollinear points, there exists exactly one plane.

Plane-Point Postulate

A plane contains at least three noncollinear points.

Plane-Line Postulate

If two points lie in a plane, then the line containing them lies in the plane.

Plane Intersection Postulate

If two planes intersect, then their intersection is a line.

Linear Pair Postulate

If two angles form a linear pair, then they are supplementary.

Properties of Segment Congruence

Segment congruence is reflexive, symmetric, and transitive.

Reflexive Property of Segment Congruence

For any segment AB, 𝐴𝐴𝐴𝐴 ≅ 𝐴𝐴𝐴𝐴.

Symmetric Property of Segment Congruence

If 𝐴𝐴𝐴𝐴 ≅ 𝐶𝐶𝐶𝐶, then 𝐶𝐶𝐶𝐶 ≅ 𝐴𝐴𝐴𝐴.

Transitive Property of Segment Congruence

If 𝐴𝐴𝐴𝐴 ≅ 𝐶𝐶𝐶𝐶 and 𝐶𝐶𝐶𝐶 ≅ 𝐸𝐸𝐸𝐸, then 𝐴𝐴𝐴𝐴 ≅ 𝐸𝐸𝐸𝐸.

Properties of Angle Congruence

Angle congruence is reflexive, symmetric, and transitive.

Reflexive Property of Angle Congruence

For any angle A, ∠𝐴𝐴 ≅ ∠𝐴𝐴.

Symmetric Property of Angle Congruence

If ∠𝐴𝐴 ≅ ∠𝐵𝐵, then ∠𝐵𝐵 ≅ ∠𝐴𝐴.

Transitive Property of Angle Congruence

If ∠𝐴𝐴 ≅ ∠𝐵𝐵 and ∠𝐵𝐵 ≅ ∠𝐶𝐶, then ∠𝐴𝐴 ≅ ∠𝐶𝐶.

Right Angles Congruence Theorem

All right angles are congruent.

Congruent Supplements Theorem

If two angles are supplementary to the same angle (or to congruent angles), then they are congruent.

Congruent Complements Theorem

If two angles are complementary to the same angle (or to congruent angles), then they are congruent.

Vertical Angles Congruence Theorem

Vertical angles are congruent.

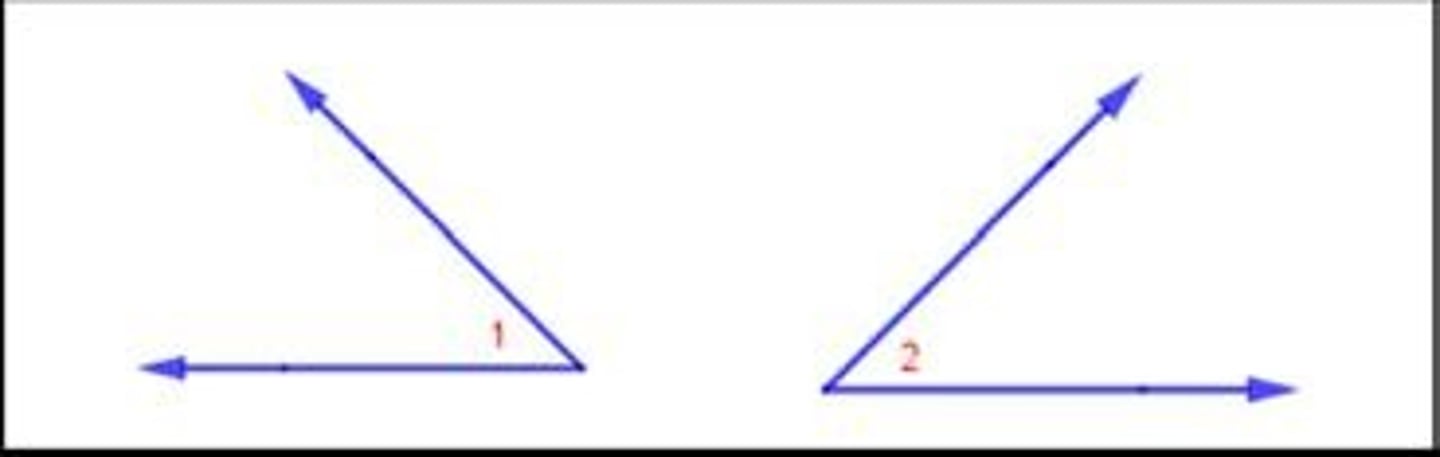
Addition Property of Equality

If a = b, then a + c = b + c.

Subtraction Property of Equality

If a = b, then a - c = b - c.

Multiplication Property of Equality

If a = b, then a∙𝑐 = 𝑏∙𝑐, 𝑐≠0.

Division Property of Equality

If a = b, then 𝑎/𝑐 = 𝑏/𝑐, c ≠0.

Substitution Property of Equality

If a = b, then a can be substituted for b (or b for a) in any equation or expression.

Distributive Property

a(b + c) = ab + ac.

Law of Detachment

If the hypothesis of a true conditional statement is true, then the conclusion is also true.

Law of Syllogism

If hypothesis p, then conclusion q. If hypothesis q, then conclusion r. If these statements are true, then this last statement is true.

Two-Column Proof

In a proof, you make one statement at a time until you reach the conclusion.

Proof of the Symmetric Property of Angle Congruence

Given: ∠1 ≅ ∠2; Prove: ∠2 ≅ ∠1.

Statements in Proofs

Statements based on facts that you know or on conclusions from deductive reasoning.

Reasons in Proofs

Definitions, postulates, or proven theorems that allow you to state the corresponding statement.

Symmetric Property of Equality

If a = b, then b = a.

Reflexive Property

For any real number a, a = a.

Transitive Property

If a = b and b = c, then a = c.

Real Numbers

Numbers that include all the rational and irrational numbers.

Segment Lengths

The distance between two points on a line segment.

Angle Measures

The measure of an angle in degrees or radians.

Reflexive Property of Congruence

For any angle ∠A, ∠A ≅ ∠A.

Symmetric Property of Congruence

If ∠A ≅ ∠B, then ∠B ≅ ∠A.

Transitive Property of Congruence

If ∠A ≅ ∠B and ∠B ≅ ∠C, then ∠A ≅ ∠C.