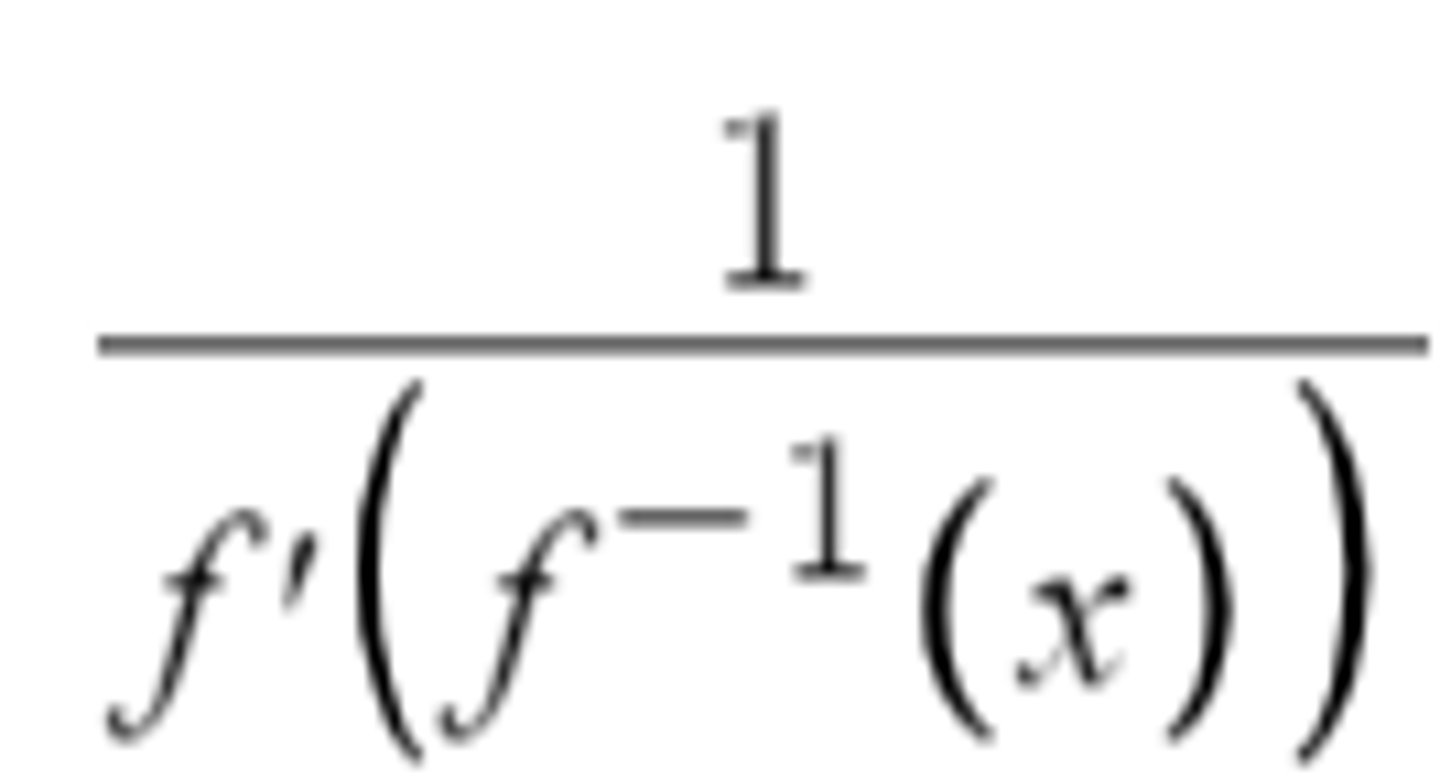Derivatives

Limit definition

lim (∆x→0) = [f(x+∆x) - f(x)]/[∆x]

Constant rule

d/dx (Constant) = 0

Power rule

d/dx (axⁿ) = naxⁿ⁻¹

Sum-difference rule

d/dx [f(x) + g(x)] = f'(x) + g'(x)

Product rule

d/dx [f(x)*g(x)] = f'(x)g(x) + f(x)g'(x)

Quotient rule

d/dx [f(x)/g(x)] = [f'(x)g(x) - f(x)g'(x)]/[g(x)²]

Chain rule

d/dx [f(g(x)] = f'(g(x))*g'(x)

Derivative of sin

d/dx sin(x) = cos(x)

Derivative of cos

d/dx cos(x) = -sin(x)

Derivative of tan

d/dx tan(x) = sec²(x)

Derivative of sec

d/dx sec(x) = sec(x)tan(x)

Derivative of cot

d/dx cot(x) = -csc²(x)

Derivative of csc

d/dx csc(x) = -csc(x)cot(x)

Natural log of x

d/dx ln x = 1/x

Natural log of u

d/dx ln u = u’/u

d/dx of sin^(-1)x

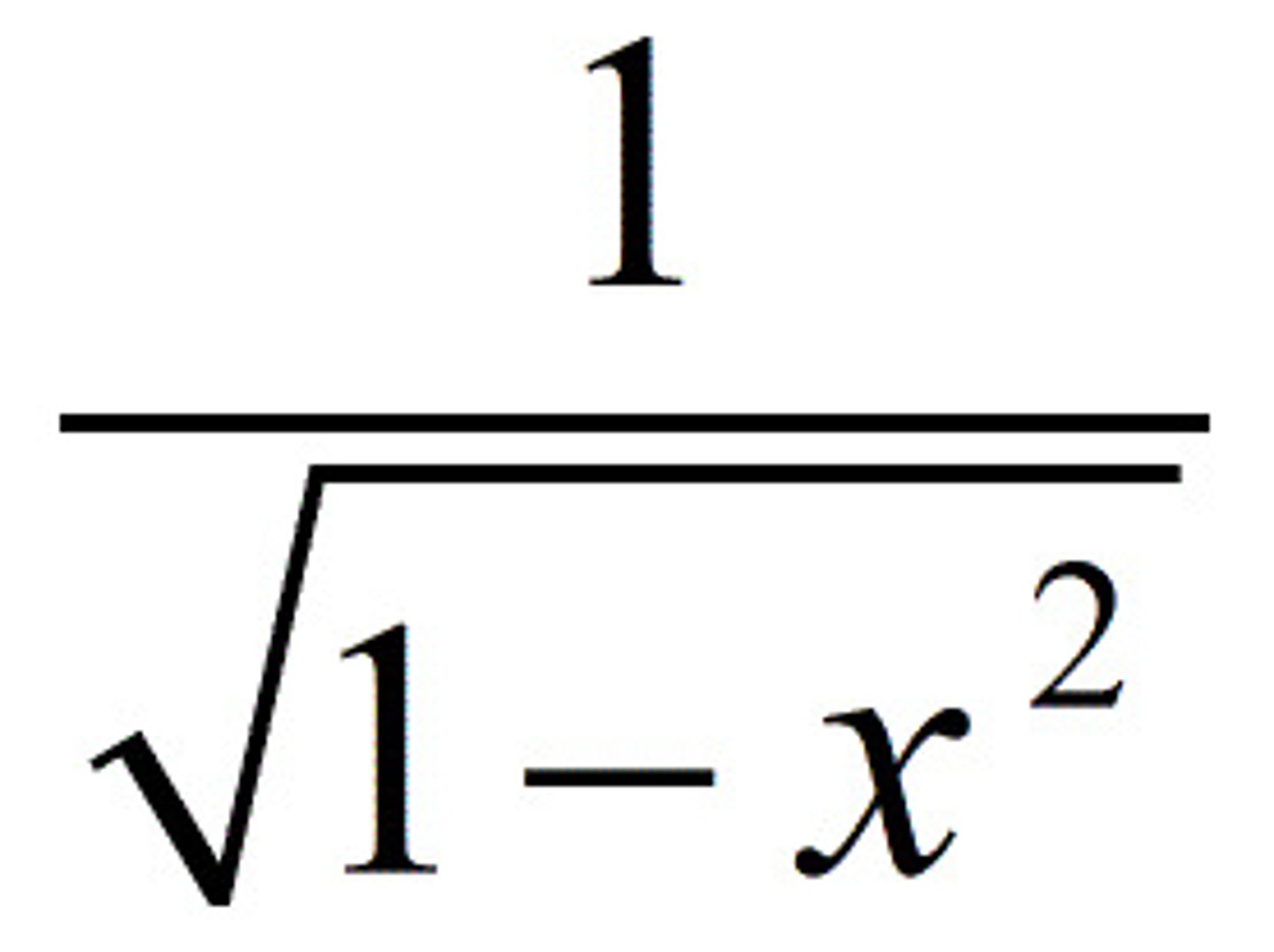
d/dx of cos^(-1)x

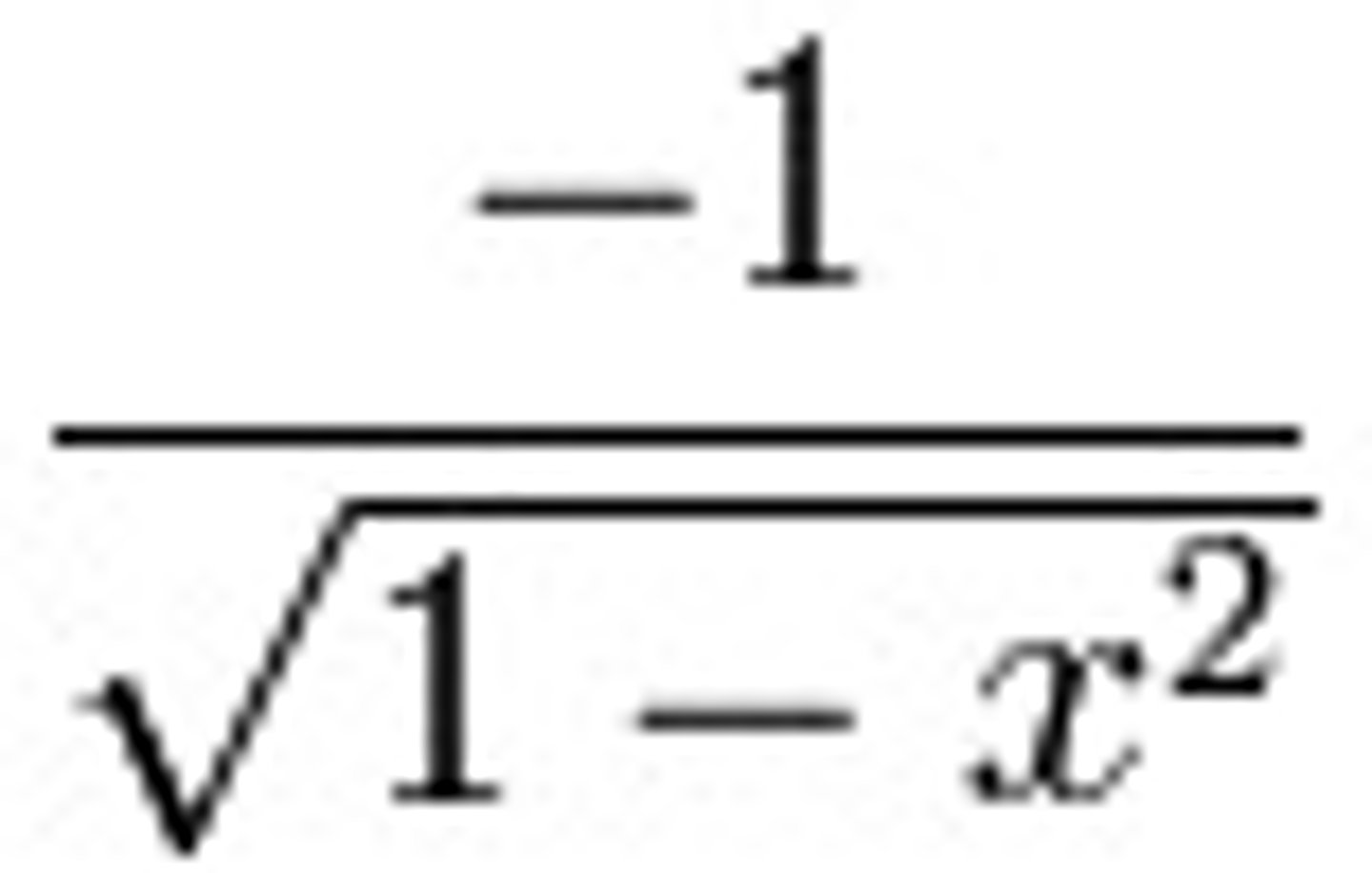
d/dx of tan^(-1)x

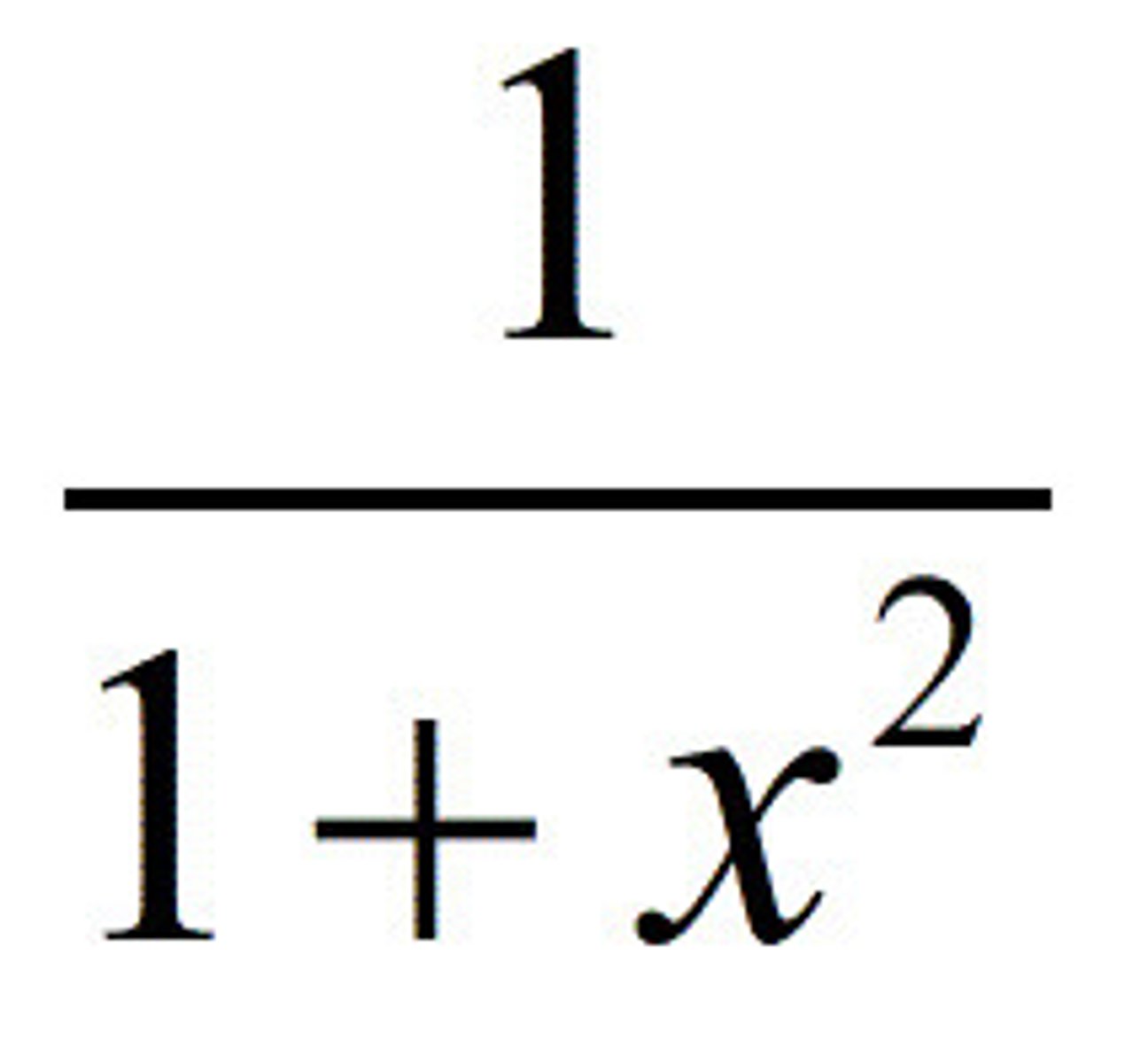
d/dx of sec^(-1)x

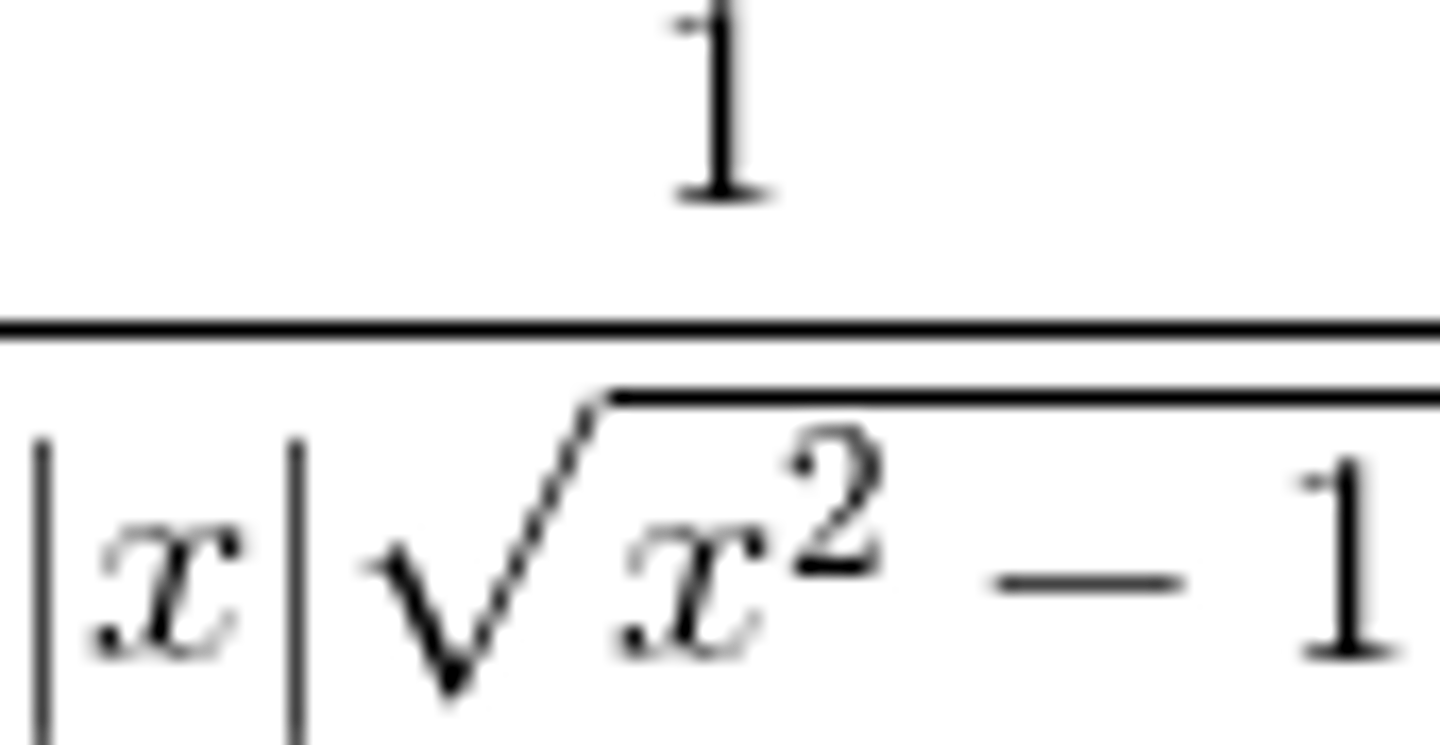
d/dx of csc^(-1)x

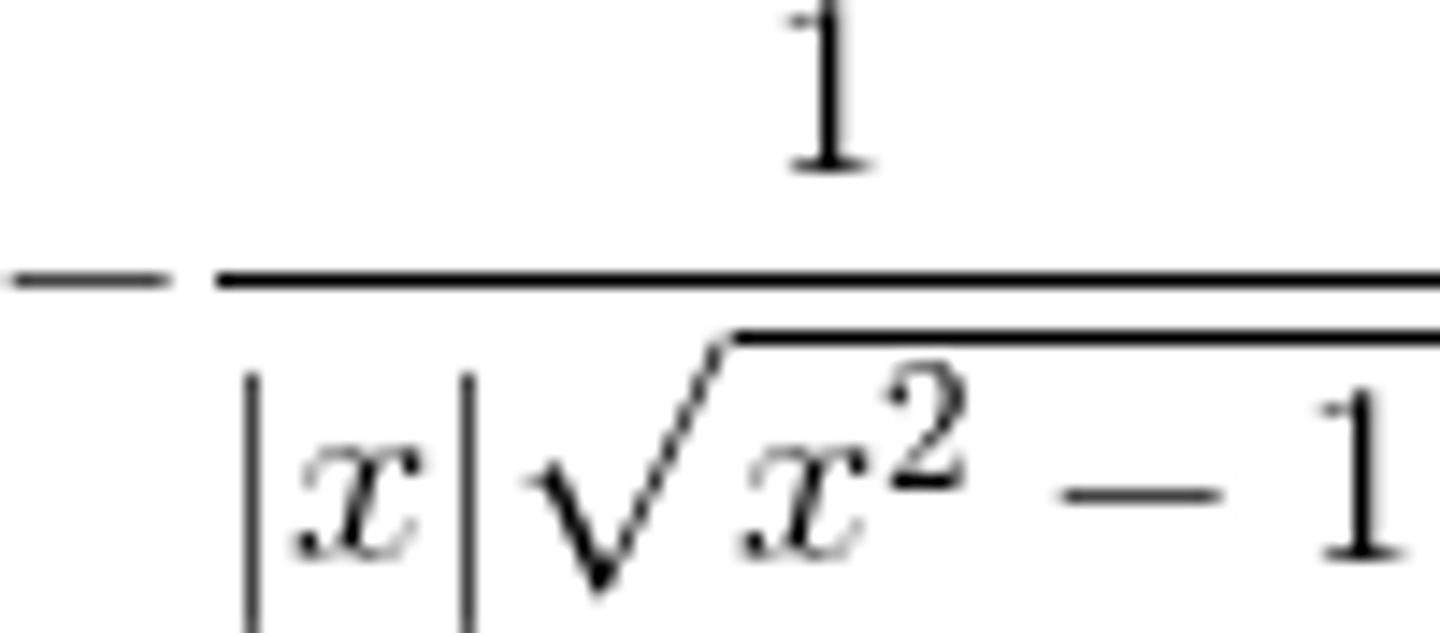
d/dx of cot^(-1)x

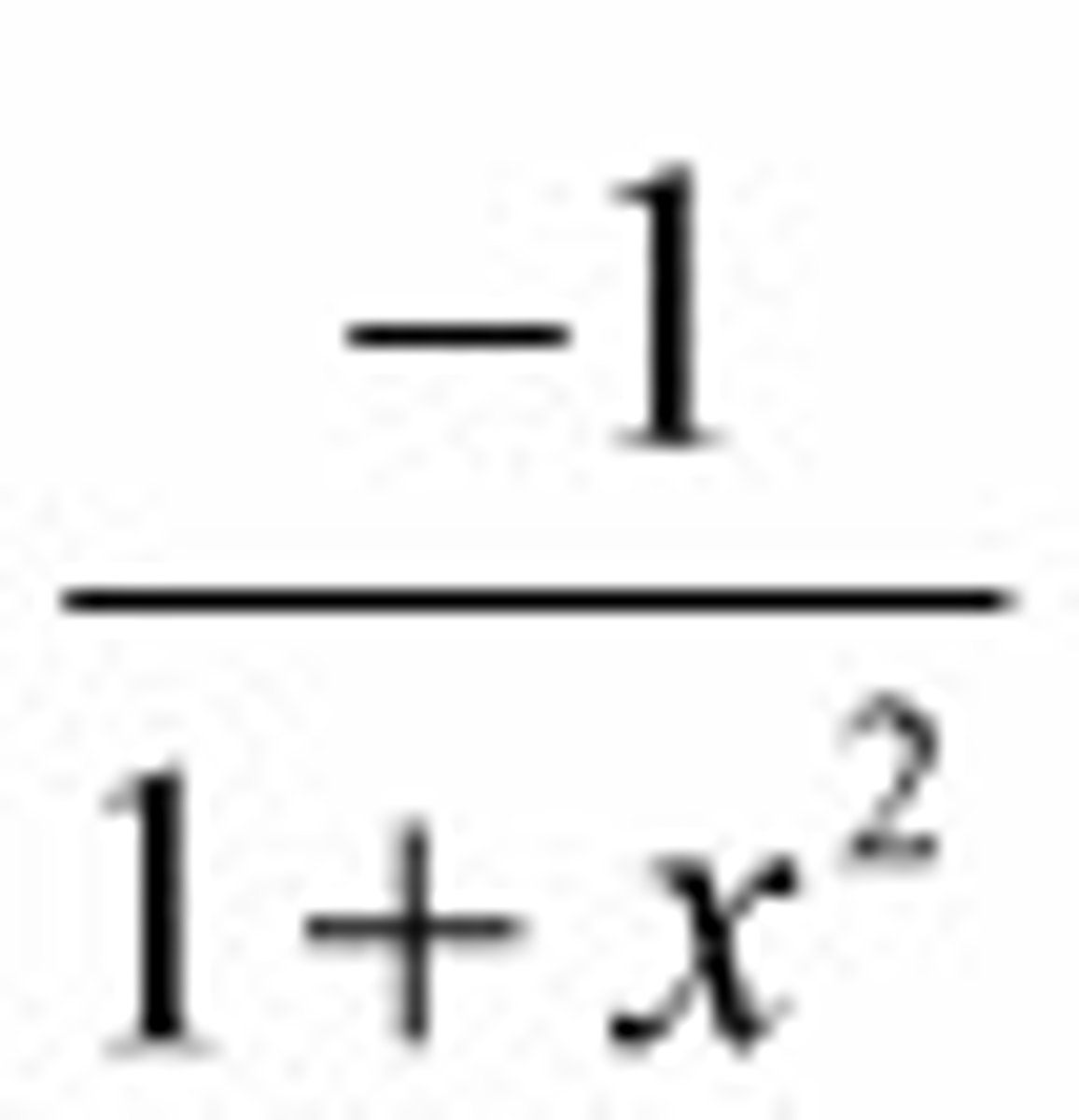
d/dx of f^-1(x)