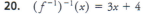Math - unit 1.3 - 1.5

Sketch the graphs of f(x) = x and g(x) = 1/x on the same axes. What do the graphs have in common? What is different about the graphs? Write equations for the asymptotes of the reciprocal function. Also name the types of functions

• f(x)=x → Linear

• g(x) = 1/x → reciprocal

• Both graphs lie in quadrant 1 and 3

• Graphs of g(x) is in two curved parts and does not intersect axes while f(x) does

• VA of g(x): x = 0 HA of g(x): g(x) = 0

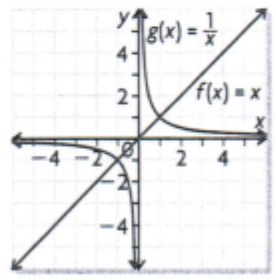
Sketch the graphs of f(x) = x² and g(x) = |x| on the same axes. Describe how these graphs are alike and how they are different. Also name thefunctions

• f(x) → Quadratic

• g(x) → absolute

• Both graphs lie in quadrant 1 and 2

• Graph of f(x) curves while g(x)is formed by two straight lines

Sketch the graphs of f(x) = x²for values x ≥ 0. On the same axes,sketch the graphs of g(x) = √x and h(x)= x. Describe how the three graphs are related. Also name the functions

• f(x) - > quadratic

• g(x) → square root

• h(x) → Linear

• Graph of g(x) is a reflection of graph f(x) in graph h(x)

State the domain and range and whether or not the relation is a function

• D = {-3, -2, -1, 0, 1, 2, 3}

• R = {-2, -1, 0, 1, 2, 3, 4}

• Is a function

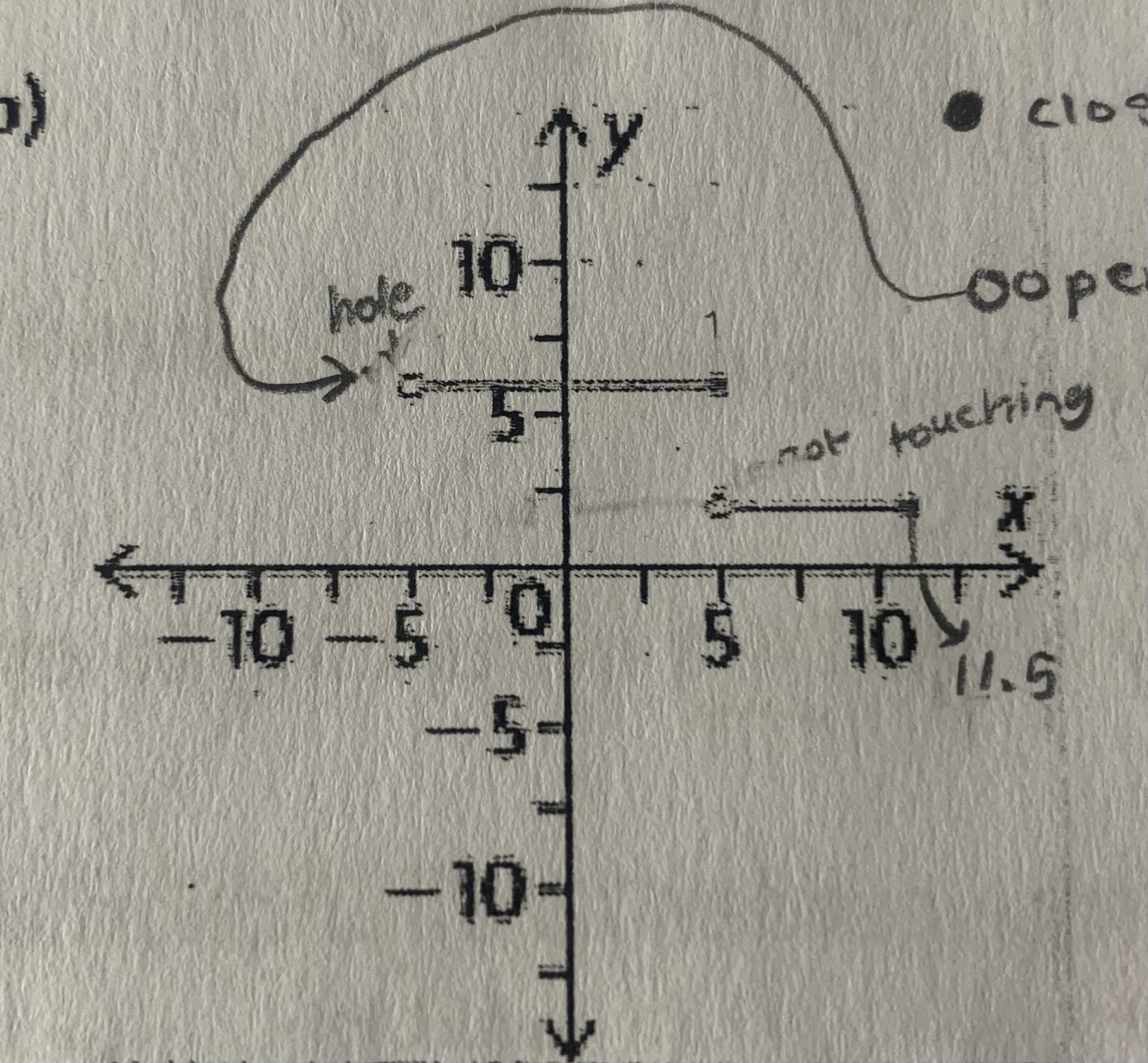
State the domain and range and whether or not the relation is a function

• x ← (-5, 11.5] or D = {xER| -5 ≤ x ≤ 11.5}

• R = {2, 5}

• Is a function

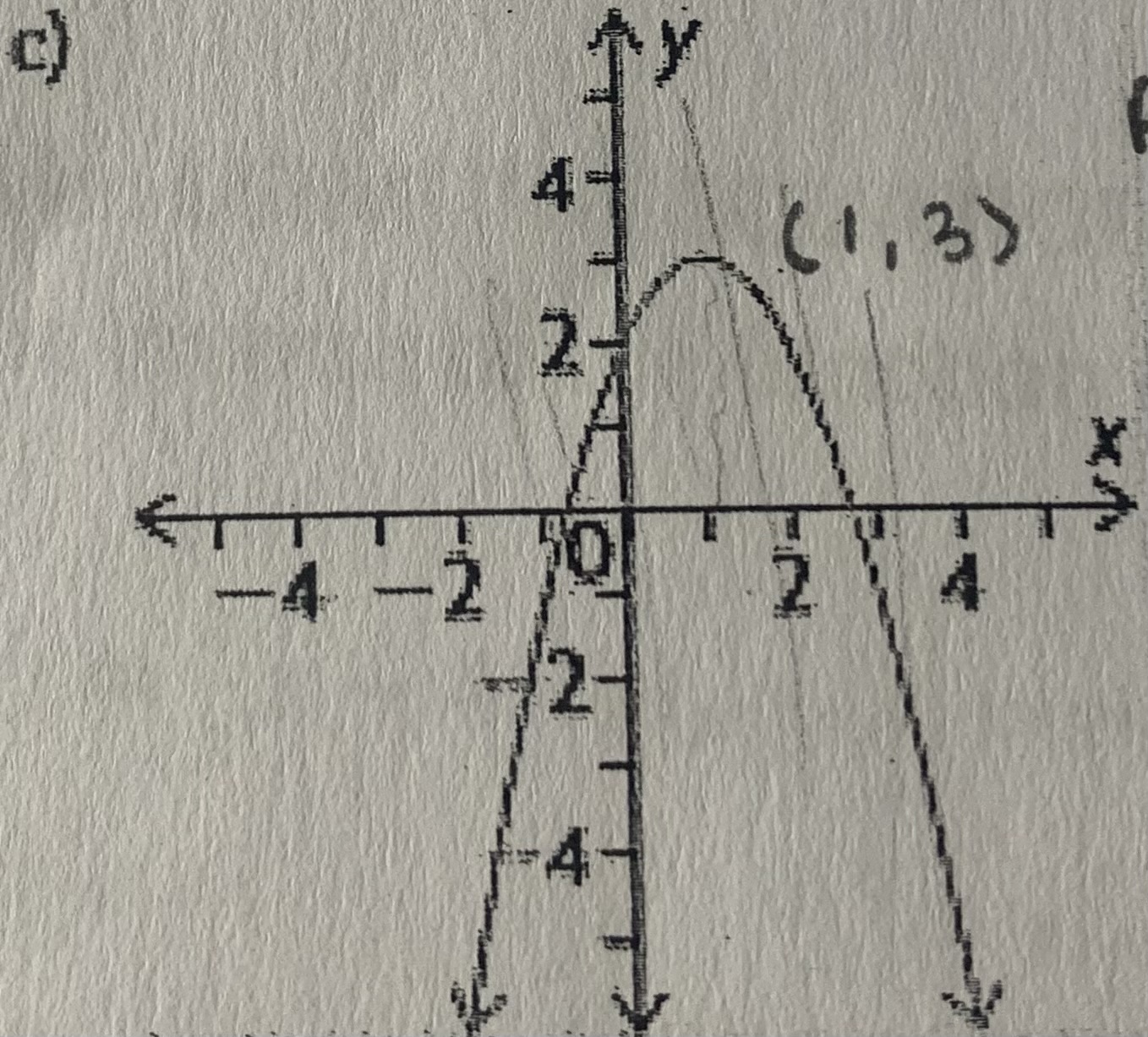
State the domain and range and whether or not the relation is a function

• D = {xER}

• R = {yER | y ≤ 3}

• Is a function

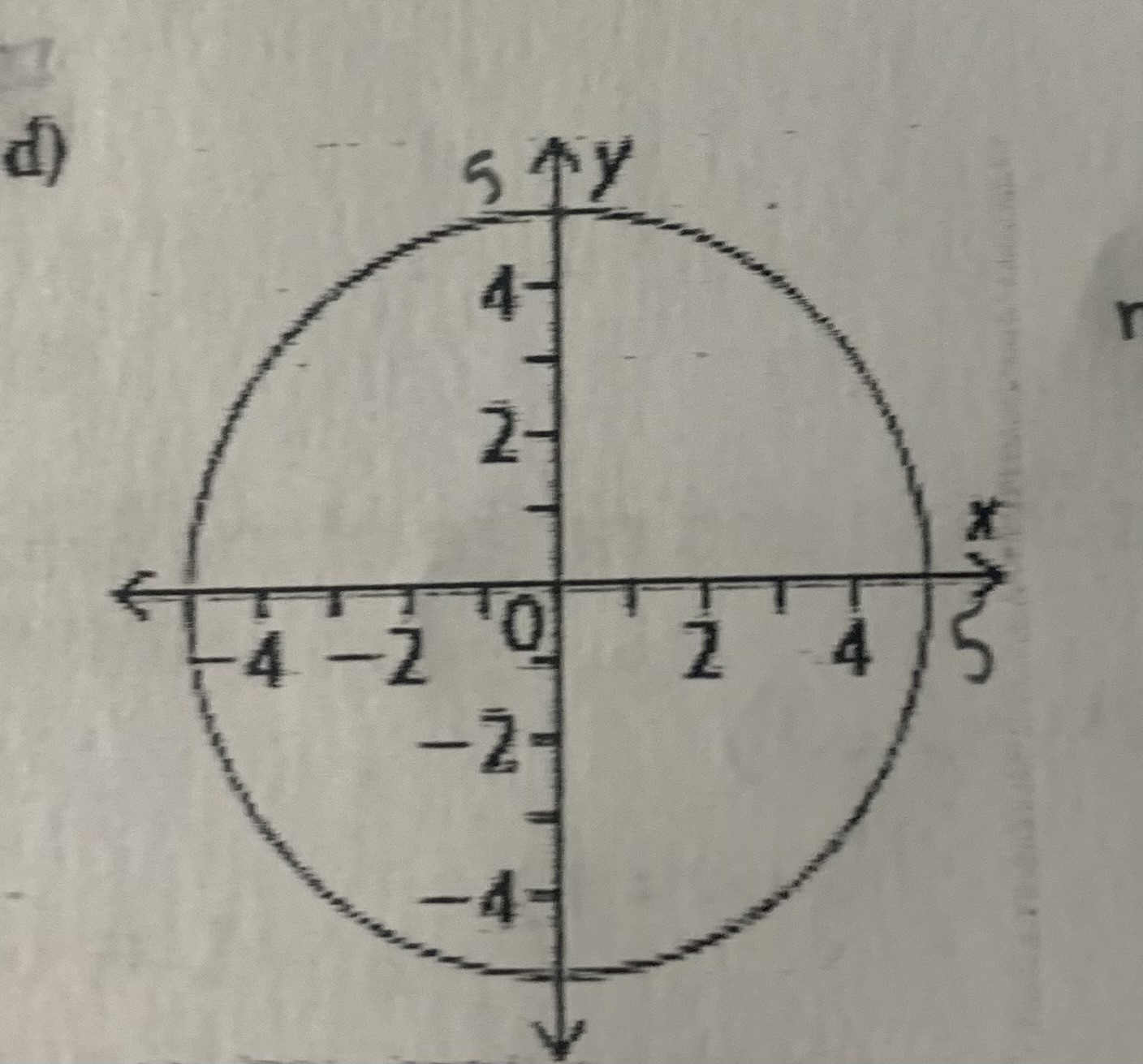
State the domain and range and whether or not the relation is a function

• D = {xER | -5 ≤ x ≤ 5} or x ← [5, -5]

• R = {yER | -5 ≤ y ≤ 5}

• Not a function

Determine the domain and range of each function

a) f(x) = 2x - 3

b) g(x) = -3(x + 1)² + 6

c) h(x) = √x - 2

a) D = {xER} R = {yER}

b) D = {xER} R = {yER | y ≤ 6}

c) D = {xER | x ≥ 2} R = {yER | y ≥ 0}

Vitaly and Sherry have 24m of fencing to enclose a rectangular garden at the back of their house.

a) express the area of the garden asa function of its width

b) determine the domain and range of the area function

a) A(w) = -2w² + 24w

b) D = {wER | 0 ≤ w ≤ 12} R = {A(w)ER | 0 ≤ A(w) ≤ 72}

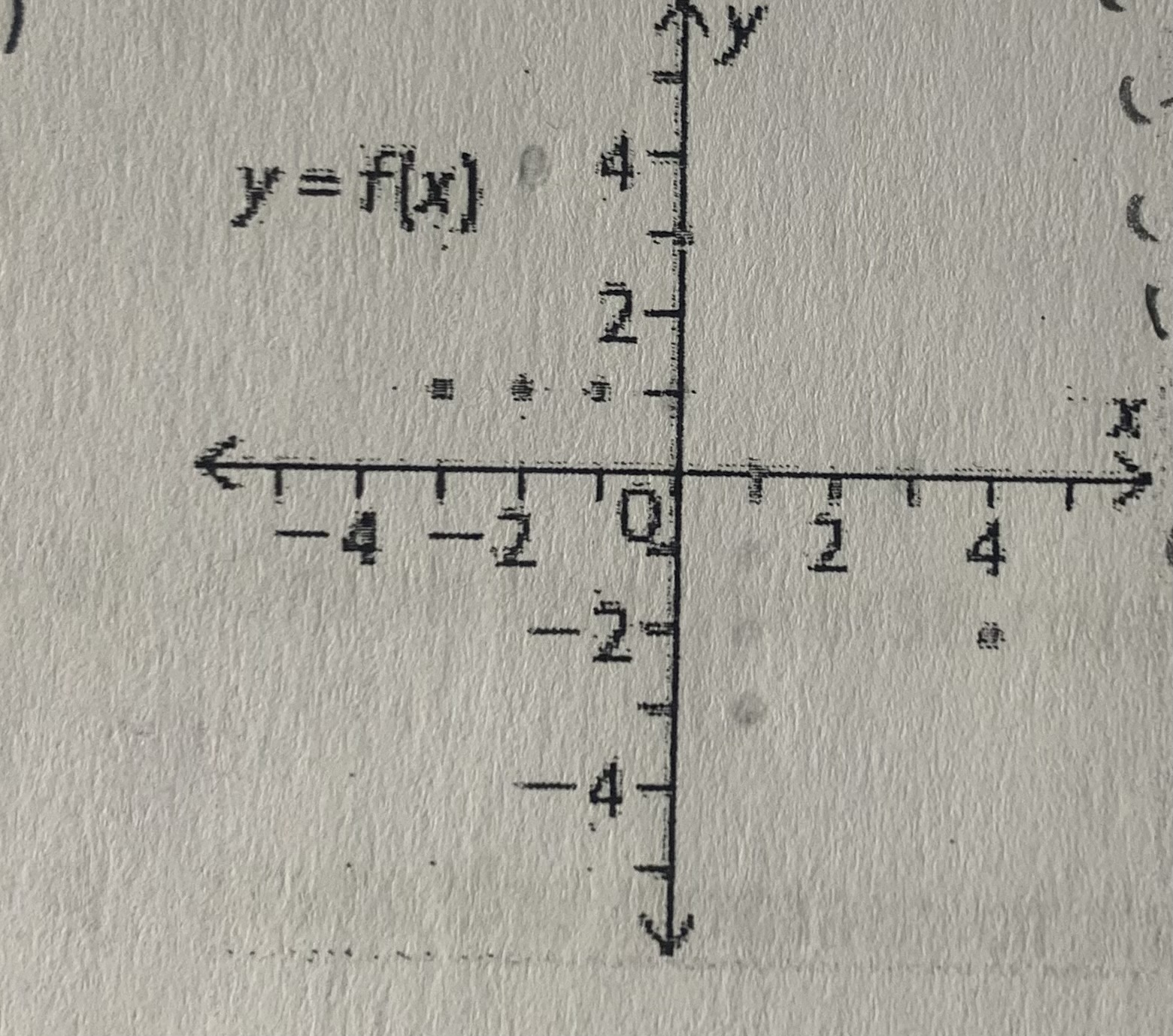
Use the graph of the function to obtain the graph of the inverse. Is the inverse a function?

• Not a function

• doesn’t pass VLT

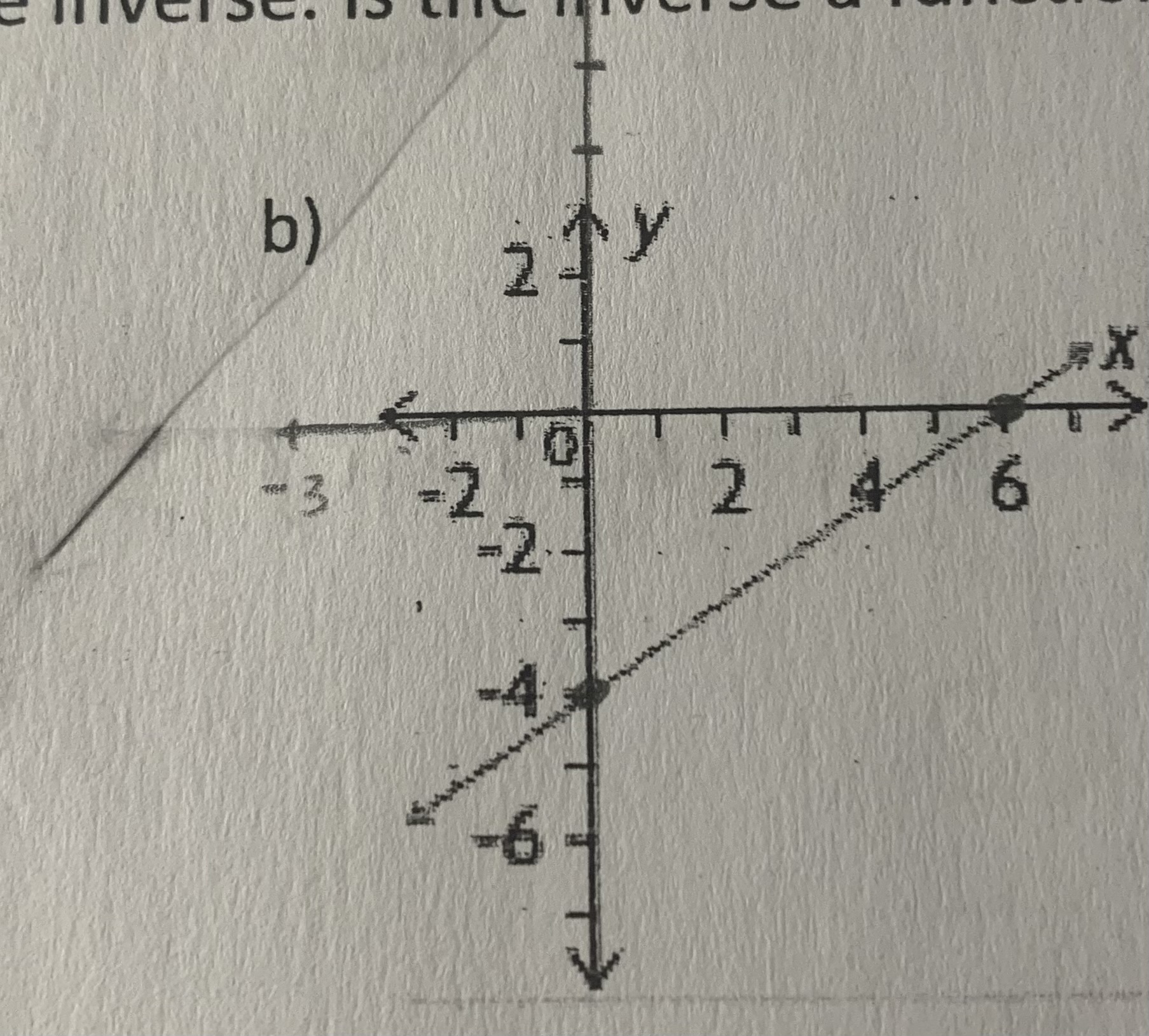
Use the graph of the function to obtain the graph of the inverse. Is the inverse a function?

• Is a function

• passes VLT

Find the inverse of the function defined by the following. Is the inverse a function?

a) f(x) = 2/3x - 4

b) f(x) = 2 - 5x

a) f(x) = 3/2(x + 4)

b) f(x) = x - 2 / -5

The temperature below Earth’s surface is a function of depth and can be defined by T(d) = 11 + 0.015d

a) State the domain and range of T(d)

b) Determine the equation for the depth in terms of temperature

c) State the domain and range of the equation in part b)

a) D = {dER | d ≥ 0} R = {T(d) ER | T(d) ≥ 11}

b) d(T) = T - 11/ 0.015

c) D = {TER | T ≥ 11} R = {dER | d ≥ 0}

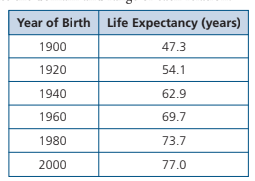
State the domain and range of the relation. Is this a function?

• D = {1900, 1920, 1940, 1960, 1980, 2000}

• R = {47.3, 54.1, 62.9, 69.7, 73.7, 77.0}

• This is a function

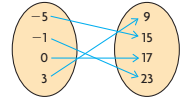
State the domain and range of the relation. Is this a function?

• D = {-5, -1, 0, 3}

• R = {9, 15, 17, 23}

• This is a function

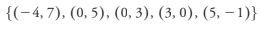
State the domain and range of the relation. Is this a function?

• D = {-4, 0, 3, 5}

• R = {-1, 0, 3, 5, 7}

• Not a function

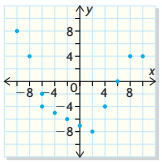
State the domain and range of the relation. Is this a function?

• D = {0, ±2, ±4, ±6, ±8, ±10}

• R = {-8, -7, -6, -5, -4, -2, 0, 4, 8}

• Not a function

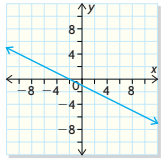
State the domain and range of the relation. Is this a function

• D = {xER}

• R = {yER}

• This is a function

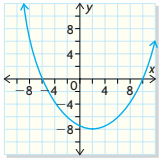
State the domain and range of the relation. Is this a function

• D = {xER}

• R = {yER | y ≥ -8}

• This is a function

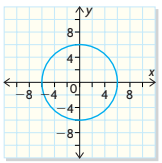
State the domain and range of the relation. Is this a function?

• D = {xER | -6 ≤ x ≤ 6}

• R = {yER | -6 ≤ y ≤ 6}

• This is not a function

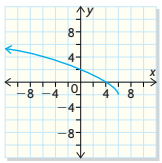
State the domain and range of the relation. Is this a function?

• D = {xER | x ≤ 6}

• R = {yER | y ≥ -2}

• This is a function

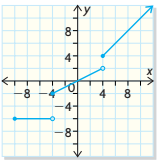
State the domain and range of the relation. Is this a function

• D = {xER | x ≥ -10}

• R = {yER | y = -6, -2 ≤ y < 2, y > 4}

• This is a function

Determine the domain and range of the function f() = 2(x - 1)² - 3 by sketching its graph

• D = {xER}

• R = {yER | y ≥ -3}

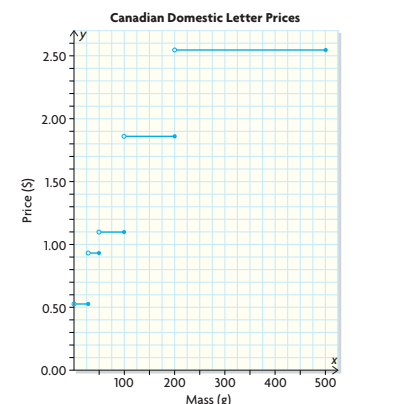
The graphs shows how 2007 prices for mailing letters in Canada vary with mass

a) explain why this relation is function. why is it important for this to be so?

b) state the domain and range of the function

a) even at masses when the price changes, a single price (the lower one) is assigned. It would not make sense to assign two or more prices to the same mass

b) D = {xER | 0 < x ≤ 500 } R = {0.52, 0.93, 1.20, 1.86, 2.55}

The route for a marathon is 15km long. Participants can walk, jog, run, or cycle. Copy and complete the table to show times for completing the marathon at different speeds.

Graph the relation in the table and explain how you know that it is a function. State the domain and range of the function

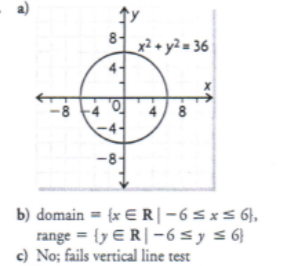
A relation is defined by x² + y² = 36

a) Graph the relation

b) State the domain and range of the relation

c) Is the relation a function? Explain

Write a function to describe coffee dripping into a 10-cup carafe at a rate of 1 mL/s. State the domain and range of the function (1 cup = 250 mL)

• V(t) = t

• D = {tER | 0 ≤ t ≤ 2500}

• R = {V(t)ER | 0 ≤ V(t) ≤ 2500)

Determine the domain and range of each function

a) f(x) = -3x + 8

b) g(x) = -0.5(x + 3)² + 4

c) h(x) = √x - 1

d) p(x) = 2/3(x -2)² - 5

e) q(x) = 11 - 5/2x

f) r(x) = √5 - x

a) D = {xER} R = {yER}

b) D = {xER} R = {yER | y ≤ 4}

c) D = {xER} R = {yER | y ≥ 0}

d) D = {xER} x ≥ 1} R = {yER | y ≥ -5}

e) D = {xER} R = {yER}

f) D = {xER | x ≤ 5} R = {yER | y ≥ 0}

A ball is thrown upward from the roof of a 25m building. The ball reaches a height of 45m above the ground after 2s and hits the ground 5s after being thrown

a) Sketch a graph that shows the height of the ball as a function of time

b) State the domain and range of the function

c) Determine an equation for the function

Write the domain and range of each function in set notation

a) f(x) = 4x + 1

b) f(x) = √x - 2

c) f(x) = 3(x + 1)² - 4

d) f(x) = -2x² - 5

a) D = {xER} R = {yER]

b) D = {xER | x ≥ 2} R = {yER| y ≥ 0}

c) D = {xER} R = {yER | y ≥ -4}

d) D = {xER} R = {yER | y ≤ -5}

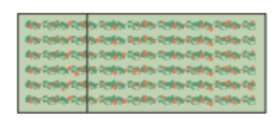
A farmer has n450m of fencing to enclose a rectangular area and divide it into two sections as shown

a) Write an equation to express the total area enclosed as a function of the width

b) Determine the domain and range of this area function

c) Determine the dimensions that give the maximum area

a) A = (450 - 3w / 2)w

b) D = {wER | 0 < w < 150} R = {AER | 0 < A ≤ 8437.5}

c) l = 112.5m w = 75m

Determine the range of each function if the domain is {-3, -1, 0, 2.5, 6}

a) f(x) = 4 - 3x

b) f(x) = 2x² - 3x + 1

a) R = {-14, -3.5, 4, 7, 13}

b) R = {1, 6, 28, 55}

Sketch the graph of a function whose domain is {xER} and range is {yER | y ≤ 2}

Answers vary

Sketch the graph of a relation that is not a function and whose domain is {xER | x ≥ -4} and range is {yER}

Answers vary

You can draw a square inside another square by placing each vertex of the inner square on one side of the outer square. The large square in the diagram has side length 10 units

a) Determine the area of the inscribed square as a function of x

b) Determine the domain and range of this area function

c) Determine the perimeter of the inscribed square as a function of x

d) determine the domain and range of this perimeter function

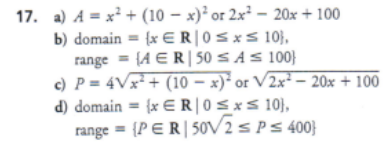
Use numerical and graphical representations to show that x² + y = 4 is a function but x² + y² = 4 is not a function

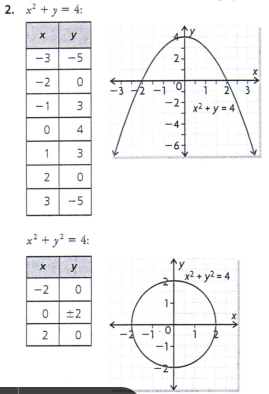
a) Graph the function f(x) = -2(x + 1)² + 3

b) Evaluate f(-3)

c) What does f(-3) represent on the graph of f

d) Use the equation to determine i) f(1) - f(0). ii) 3f(2) - 5. iii) f(2 -x)

b) f(-3) = -5

c) y-coordinate of the point on the graph with x-coordinate of -3

d) i) -6 ii) -50 iii) -2(3 - x)² + 3

A teacher asked her students to think of a number, multiply it by 5, and substract the product from 20. Then she asked them to multiply the resulting difference by the number they first thought of.

a) Use function notation to express the final answer in terms of the original number

b) Determine the Outputs for the input numbers, 1, -1, and 7

c) Determine the maximum result possible

a) A(n) = -5n² + 20n

b) 15, -25, -105

c) 20

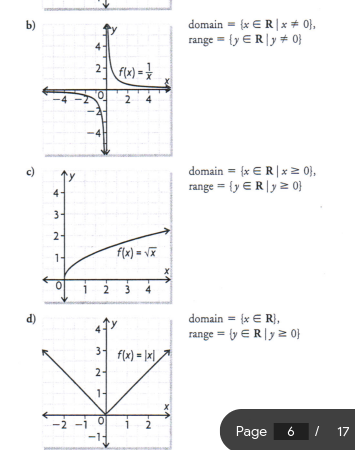
Graph each function and state its domain and range. and state the type of function

a) f(x) = x²

b) f(x) = 1/x

c) f(x) = √x

d) f(x) = |x|

a) quadratic

b) reciprocal

c) Square root

d) Absolute

A farmer has 600m of fencing to enclose a rectangular area and divide it into three sections as shown.

a) Write an equation to express the total area enclosed as a function of the width

b) Determine the domain and range of this area function

c) Determine the dimensions that give the maximum area

a) A(w) = (600 - 4w / 2)w

b) D = wER | 0 < w < 150} R = {A(w)ER | 0 < A(w) ≤ 11250}

c) l = 150m w = 75m

Determine the domain and range for each

a) A parabola has a vertex at (-2, 5), and y = 5 is its maximum value

b) A parabola has a vertex at (3, 4) and y = 4 is its minimum value

c) A circle has a centre at (0,0) and a radius of 7

d) A circle has a centre at (2, 5) and a radius of 4

a) D = {xER } R = {yER | y ≤ 5}

b) D = {xER} R = {yER | y ≥ 4}

c) D = {xER | -7 ≤ x ≤ 7} R = {yER | -7 ≤ y ≤ 7}

d) D = {xER | -2 ≤ x ≤ 6} R = {yER | 1 ≤ y ≤ 9}

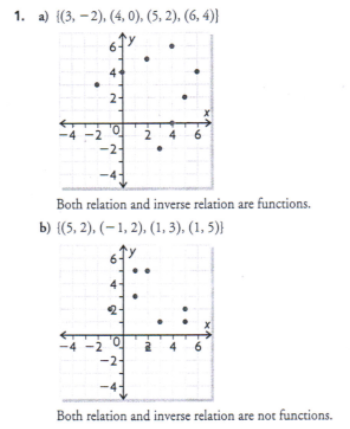
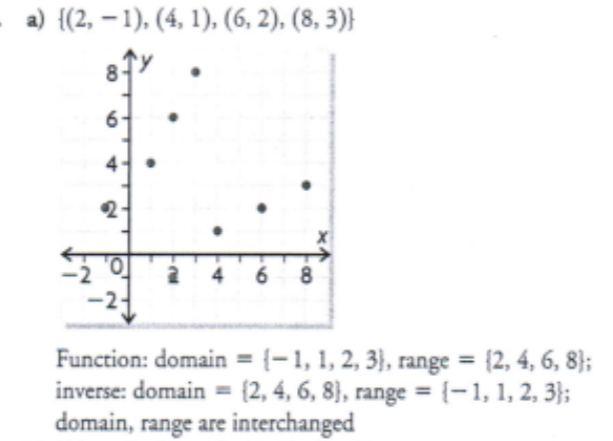
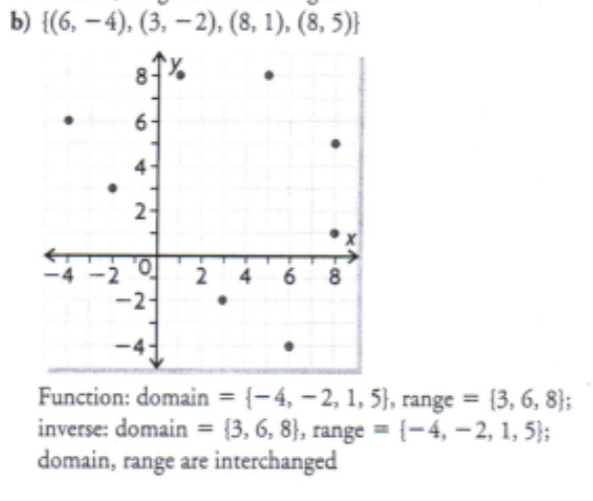
Determine the inverse relation for each set of ordered pairs. Graph each relation and its inverse. Which of the relations and inverse relations are functions?

a) {(-2, 3), (0, 4), (2, 5), (4, 6)}

b) {(2, 5), (2, -1), (3, 1), (5, 1)}

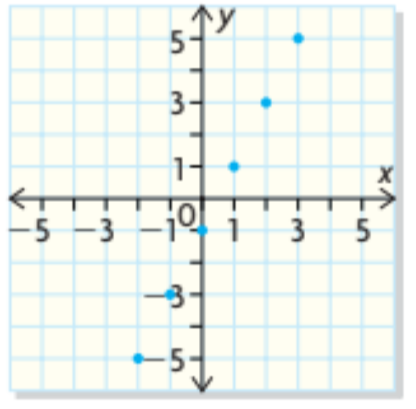
Copy the graph of the function and graph its inverse. For the graph, identify the points that are common to the function and its inverse. Is it a function?

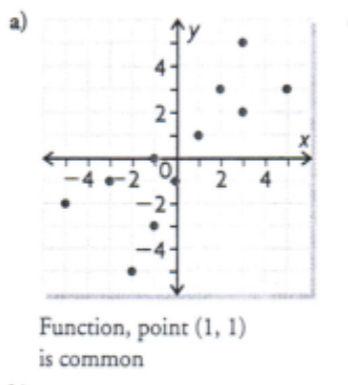
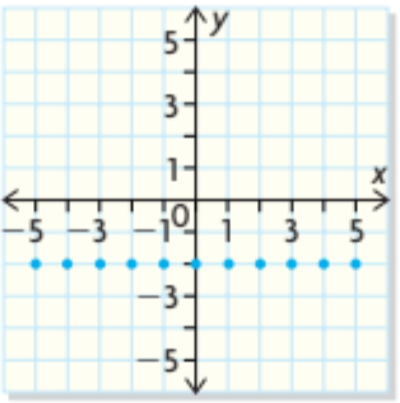
Copy the graph of the function and graph its inverse. For the graph, identify the points that are common to the function and its inverse. Is it a function?

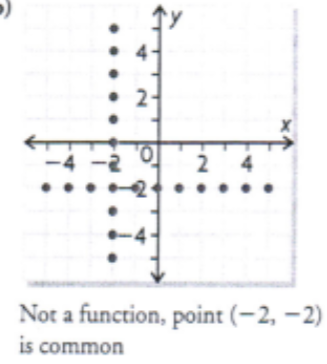
Copy the graph of the function and graph its inverse. For the graph, identify the points that are common to the function and its inverse. Is it a function?

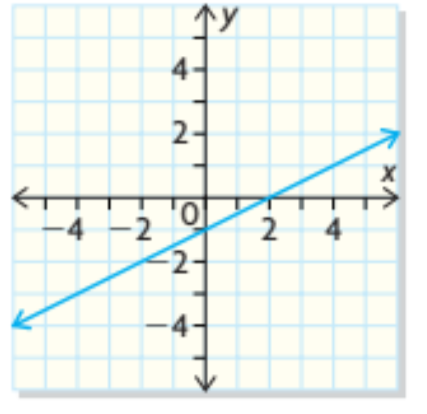
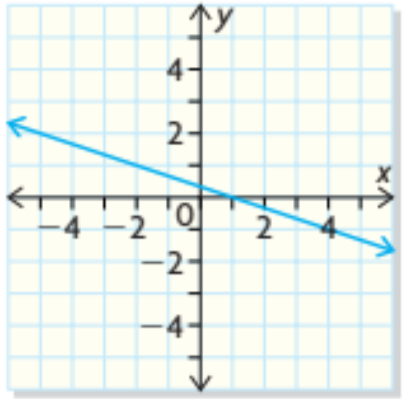
Copy the graph of the function and graph its inverse. For the graph, identify the points that are common to the function and its inverse. Is it a function?

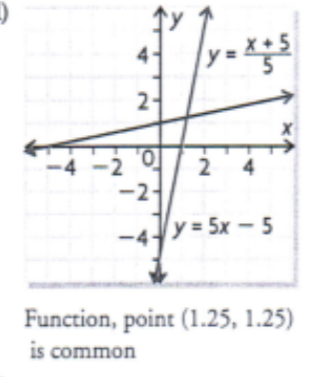
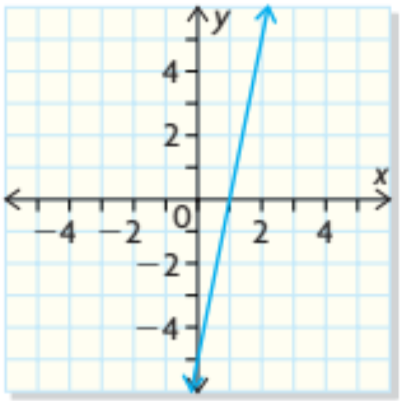
Copy the graph of the function and graph its inverse. For the graph, identify the points that are common to the function and its inverse. Is it a function?

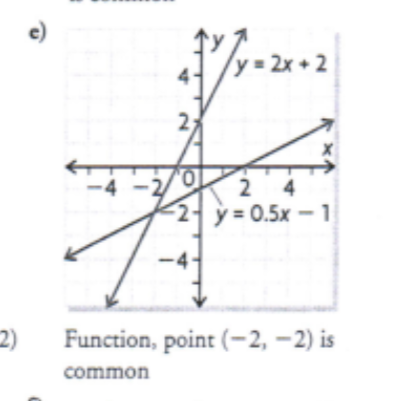
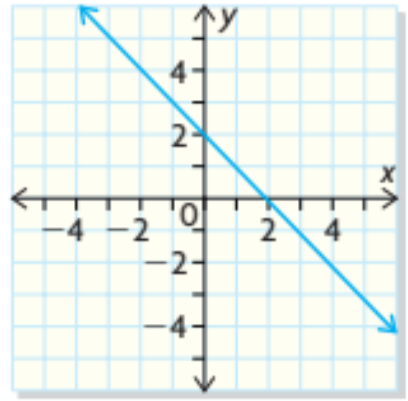
Copy the graph of the function and graph its inverse. For the graph, identify the points that are common to the function and its inverse. Is it a function?

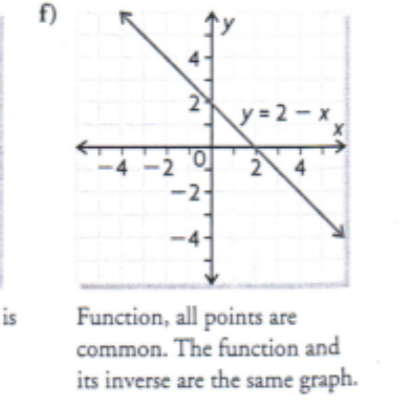
Determine whether each pair of functions described in words are inverses

a) f: Multiply by 3, then add 1. g: Divide by 3, then subtract 1

b) f: Multiply by 5, then subtract 2. g: Add 2, then divide by 5

a) No

b) Yes

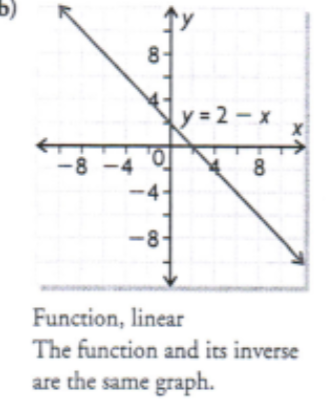
For each linear function, interchange x and y. Then solve for y to determine the inverse.

a) y = 4x - 3

b) y = 2 - 1/2x

c) 3x + 4y = 6

d) 2y - 10 = 5x

a) y = (x + 3) / 4

b) y = 2(2 - x)

c) y = (6 - 4x) / 3

d) y = (2x - 10) / 5

Determine the inverse of each linear function by reversing the operations

a) f(x) = x - 4

b) f(x) = 3x + 1

c) f(x) = 5x

d) f(x) = 1/2x - 1

e) f(x) = 6 - 5x

f) f(x) = 3/4x + 2

a) f^-1(x) = x + 4

b) f^-1(x) = (x - 1) / 3

c) f^-1(x) = 1/5x

d) f^-1(x) = 2(x + 1)

e) f^-1(x) = 6 - x / 5

f) f^-1(x) = 4/3(x - 2)

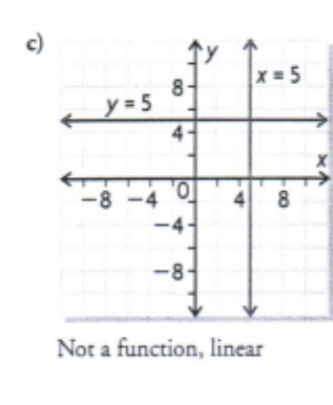
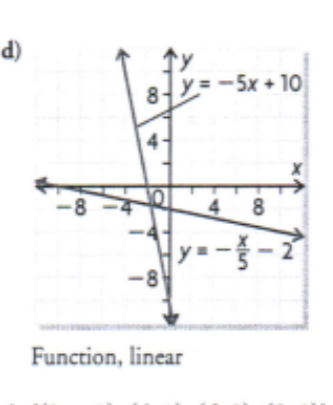
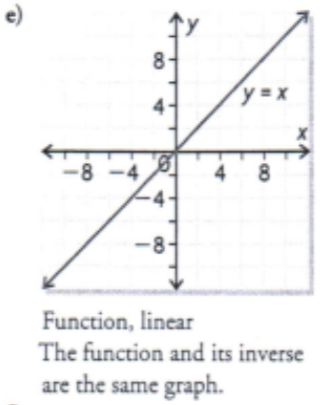
Determine the inverse of each linear function by interchanging the variables

a) f(x) = x + 7

b) f(x) = 2 - x

c) f(x) = 5

d) f(x) = -1/5x - 2

e) f(x) = x

f) f(x) = (x - 3) / 4

a) f^-1(x) = x - 7

b) f^-1(x) = 2 - x

c) x = 5

d) f^-1(x) = -5(x + 2)

e) f^-1(x) = 4x + 3

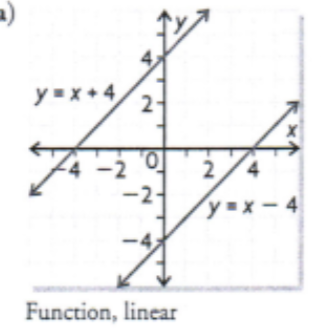
Determine the inverse of the linear function by reversing the operations. Then graph it and determine if its a function

f(x) = x - 4

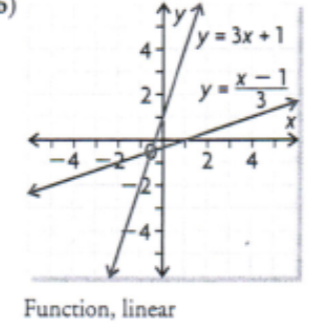
Determine the inverse of the linear function by reversing the operations. Then graph it and determine if its a function

f(x) = 3x + 1

Determine the inverse of the linear function by reversing the operations. Then graph it and determine if its a function

f(x) = 5x

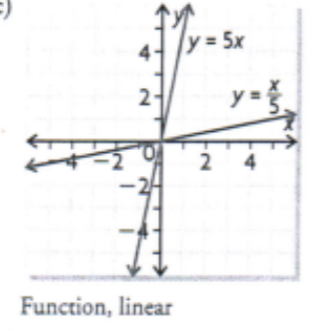
Determine the inverse of the linear function by reversing the operations. Then graph it and determine if its a function

f(x) = 1/2x - 1

Determine the inverse of the linear function by reversing the operations. Then graph it and determine if its a function

f(x) = 6 - 5x

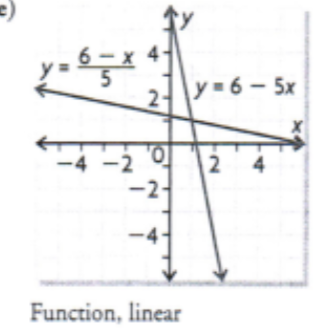
Determine the inverse of the linear function by reversing the operations. Then graph it and determine if its a function

f(x) = 3/4x + 2

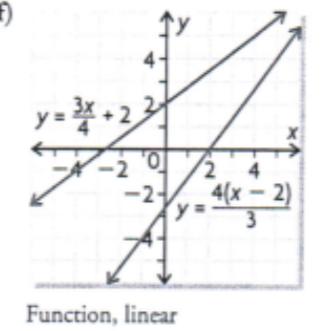
Determine the inverse of the linear function by interchanging the variables. Then graph the inverse and say if its a function

f(x) = x + 7

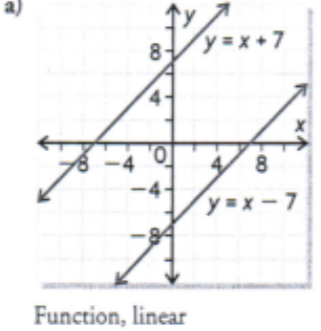
Determine the inverse of the linear function by interchanging the variables. Then graph the inverse and say if its a function

f(x) = 2 - x

Determine the inverse of the linear function by interchanging the variables. Then graph the inverse and say if its a function

f(x) = 5

Determine the inverse of the linear function by interchanging the variables. Then graph the inverse and say if its a function

f(x) = -1/5x - 2

Determine the inverse of the linear function by interchanging the variables. Then graph the inverse and say if its a function

f(x) = x

Determine the inverse of the linear function by interchanging the variables. Then graph the inverse and say if its a function

f(x) = (x - 3) / 4

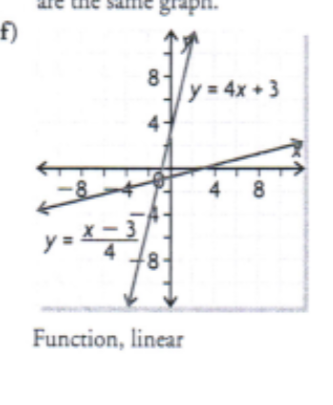
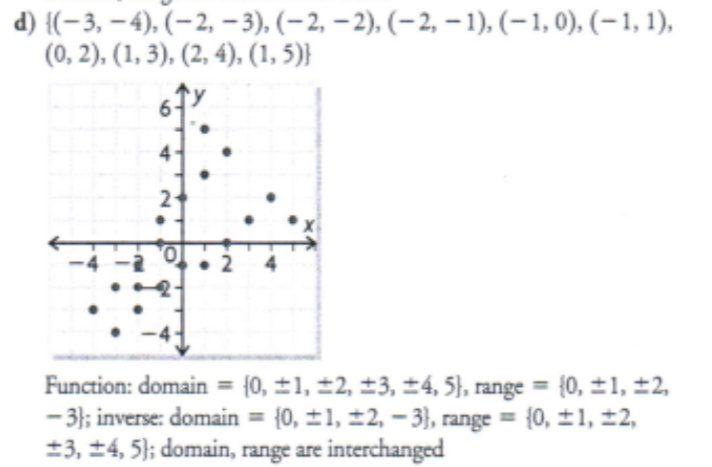
For each function, determine the inverse, sketch the graphs of the function and its inverse, and state the domain and range of both the function and its inverse. In each case, how do the domain and range of the function compare with the domain and range of the inverse

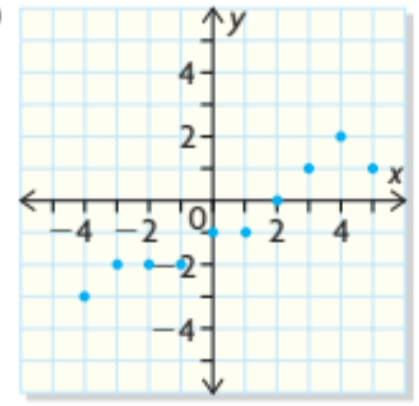
{(-1, 2), (1, 4), (2, 6), (3, 8)}

For each function, determine the inverse, sketch the graphs of the function and its inverse, and state the domain and range of both the function and its inverse. In each case, how do the domain and range of the function compare with the domain and range of the inverse

For each function, determine the inverse, sketch the graphs of the function and its inverse, and state the domain and range of both the function and its inverse. In each case, how do the domain and range of the function compare with the domain and range of the inverse

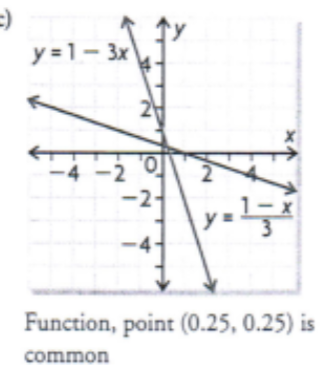
f(x) = 1 - 3x

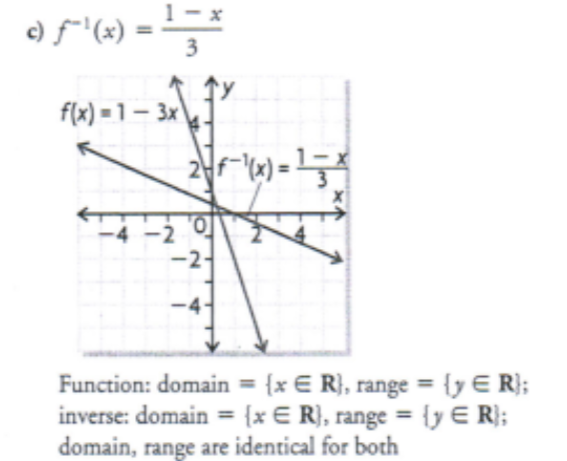
For each function, determine the inverse, sketch the graphs of the function and its inverse, and state the domain and range of both the function and its inverse. In each case, how do the domain and range of the function compare with the domain and range of the inverse

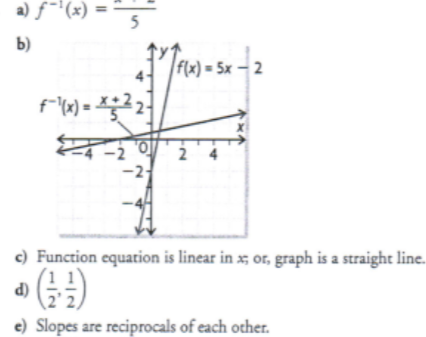
a) Determine f^-1 for the linear function f(x) = 5x - 2

b) Graph f and f^-1 on the same axes

c) Explain how you can tell that f^-1 is also a linear function

d) State the coordinated of any points that are common to both f and f^-1

e) Compare the slopes of the two lines

a) Determine f^-1 for the linear function g(x) = -1/2x + 3

b) Graph f and f^-1 on the same axes

c) Explain how you can tell that f^-1 is also a linear function

d) State the coordinated of any points that are common to both f and f^-1

e) Compare the slopes of the two lines

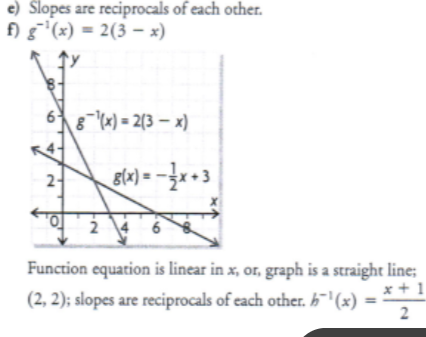
a) Determine f^-1 for the linear function h(x) = 2x - 1

b) Graph f and f^-1 on the same axes

c) Explain how you can tell that f^-1 is also a linear function

d) State the coordinated of any points that are common to both f and f^-1

e) Compare the slopes of the two lines

• h^-1(x) = x + 1 / 2

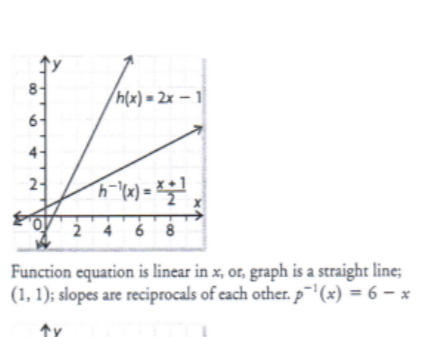
a) Determine f^-1 for the linear function p(x) = 6 - x

b) Graph f and f^-1 on the same axes

c) Explain how you can tell that f^-1 is also a linear function

d) State the coordinated of any points that are common to both f and f^-1

e) Compare the slopes of the two lines

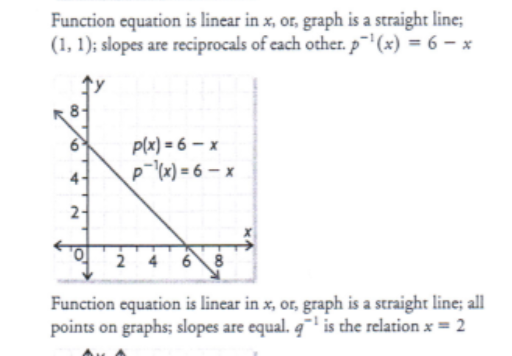
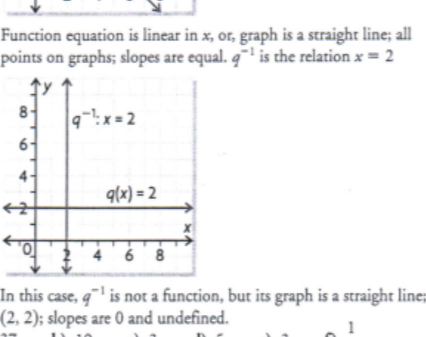
a) Determine f^-1 for the linear function q(x) = 2

b) Graph f and f^-1 on the same axes

c) Explain how you can tell that f^-1 is also a linear function

d) State the coordinated of any points that are common to both f and f^-1

e) Compare the slopes of the two lines

For g(t) = 3t - 2, determine each value

a) g(13)

b) g(7)

c) g(13) - g(7) / 13 - 7

d) g^-1(13)

e) g^-1(7)

f) g^-1(13) - g^-1(7) / 13 - 7

g) what do parts c) and (f) represent

a) 37

b) 19

c) 3

d) 5

e) 3

f) 1/3

g) c) is slope of g(t) (f) is slope of g^-1(t)

The formula for converting a temperature in degrees Celsius into degrees fahrenheit is F = 9/5C + 32. Shirelle, an American visitor to Canada, uses a simpler rule to convert from Celsius to Fahrenheit: Double the Celsius temperature, then add 30

a) Use function notation to write an equation for this rule. Call the function f and let x represent the temperature in degrees Celsius

b) Write f^-1 as a rule. Who might use this rule?

c) Determine f^-1(x)

d) One day, the temperature was 14 degrees Celsius. Use function notation to express this temperature in degrees fahrenheit

e) Another day, the temperature was 70 degrees fahrenheit. Use function notation to express this temperature in degrees celsius

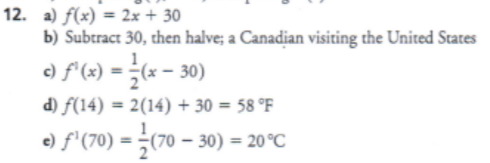
Ben, another American visitor came to Canada, uses this rule to convert centimeters to inches: multiply by 4, and then divide by 10. Let the function g be the method for converting centimetres to inches, according to Ben’s rule.

a) Write g^-1 as a rule

b) Describe a situation in which the rule for g^-1 might be useful

c) Determine g(x) and g^-1(x)

d) One day, 15 cm of snow fell. Use function notation to represent this amount in inches

e) Ben is 5 ft 10 in tall. Use function notation to represent his height in centimeters

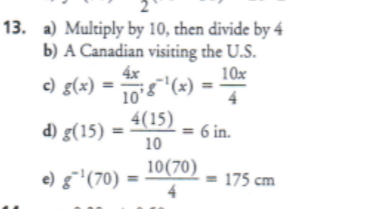
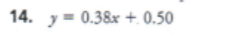
Tiffany is paid $8.05/h, plus 5% of her sales over $1000, for a 40 h work week. For example, suppose Tiffany sold $1800 worth of merchandise. Then she would earn $8.05(40) + 0.05($800) = $362

a) Graph the relation between Tiffany’s total pay for a 40 h work week and her sales for that week

b) Write the relation in function notation

c) Graph the inverse relation

d) Write the inverse relation in function notation

e) Write an expression in function notation that represents her sales if she earned $420 one work week. Then evaluate

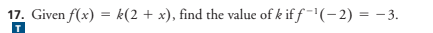
• k = 2