Research Methods II Exam 1

Population

set of all the individuals of interest in a study

Sample

the set of individuals selected for a study

Parameter

describes a characteristic of the population

Statistic

describes a characteristic of a sample

Descriptive Statistics

Statistical procedures that summarize, organize, and simplify data  (i.e. tables showing mean age and IQ)

Inferential statistics

Consists of techniques that allow us to study samples and then generalize about the populations from which they were selected

Sampling Error

Naturally occurring discrepancy or error that exists between a sample statistic and the corresponding population parameter (varies depending on sampling method, size, and conditions)

Construct

internal variable that helps describe and explain behavior that cannot be directly observed

Operational definition

external representation through which a construct will be measured or observed in a study

Discrete variables

consists of separate, indivisible categories; no values exist in between

Continuous variables

infinite number of possible values that fall between two observed values

Real limits

Boundaries of the intervals in a continuous variable

Nominal scale

names of categories without order or hierarchy

Ordinal scale

names of categories with a distinct order or hierarchy

Interval scale

arbitrary zero point (something at zero)

Ratio scale

zero is the absence of a measured trait

Correlational research

explores a potential relationship between two variables

Nonexperimental research

find strong relationships

experimental research

Finds an effect

Frequency tables

have a listed X (value obtained) and a listed f (frequency of the value); can also include an X² column, a ƒX² column

Proportion (p)

represents the fraction of the total group associated with each score (represented as p = f/n)

Percentage

Taking p and multiplying it by 100 to obtain the percent of the group associated with that score (represented as p(100))

ΣX

sum of all X values

ΣX²

sum of all X values squared

Percentiles

contextualize data

Percentile rank

how much of the data is at or below that score

Histograms

used for grouped frequencies (i.e. letter grades)

Polygons

tracks the frequency of a variable over time

Bar graphs

displays nominal data

Symmetrical distributions

distribution mirrors itself along the middle vertical axis

Negatively skewed distributions

Tail is to the left

Positively scaled distributions

Tail is to the right

Stem and leaf displays

Stem: leading digit

Leaf: last digit

Mean

average of all scores

Mean notation

M = sample mean

µ = population mean

Population mean formula

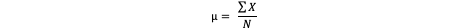
Sample mean formula

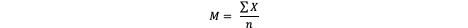
Median

midpoint in the distribution

Finding the median for an odd number of values

1. Sort the data

2. Divide the total number of values by 2 and find the rounded-up score

3. i.e. 5 values  2 = 2.5; find the third value

Find the median for an even number of values

1. Sort the data

2. Divide the total number of values by 2

3. Find that and the next score, then compute the mean between them

4. i.e. 6 values  2 = 3; find the mean of the 3^rd and 4^th values

Find the median for continuous variables

Mode

Most frequently occurring score

• In bimodal distributions (two peaks):

  • Minor mode: small valuer

  • Major mode: larger value

Alternative definitions of the mean

1. Equal distribution: score each person gets if divided equally

2. Balance point on a seesaw of values

Calculate a weighted mean

Variance (σ²)

• Measures how much scores vary

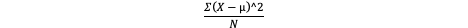
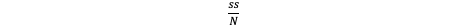
Explain measures of central tendency in symmetrical distributions

mean, median, and mode will be roughly the same

Explain measures of central tendency in skewed distributions

1. Mode: peak

2. Mean: pulled toward the tail

3. Median: between mode and mean

When to use mean to describe central tendency

Approximately symmetrical distributions

When to use median to describe central tendency

1. Outliers/skew

2. Undetermined values

3. Open-ended distributions

4. Ordinal data

When to use mode to describe central tendency

1. Nominal scales

2. Discrete variables

3. Used in addition to mean or median to describe the shape

Variability

1. difference in scores individuals obtain on a measure

2. Basis for human behavior

3. Describes score distribution

How to calculate simple range

Smallest score subtracted from the largest score

How to calculate IQR

25th percentile subtracted from the 75th percentile

Standard deviation

Average distance between a score and the mean

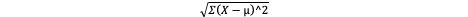
How to estimate standard deviation for a set of scores

• When looking at a frequency table of X values, subtract the mean from X

• Square that value

• Add up all of the squared values

• Find the square root

Sum of Squares Formulas

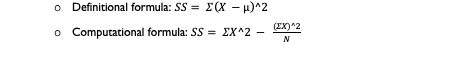
Standard Deviation for a Population

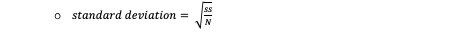
Why is variance (s²) and standard deviation (s) altered for a sample?

To allow the final score not to be restricted

SS Formulas

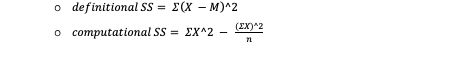
Variance for a sample formula

Z-score Formula

Probability definition

Chances a desired event occurs out of chances of everything occurring (can be expressed as a fraction, decimal, or percentage)

IQR for a normal distribution

• 25^th percentile: -0.67

• 75^th percentile: 0.67

Characteristics of Distributions for Sample Means

• Distribution: bell curve

• Sample means are relatively close to the population means

• Sample means will get closer to µ the larger the sample size

Central Limit Theorem

A distribution always tends toward a normal shape as n increases

Standard Error Formula

Standard deviation of a sample population

Z-Score formula for a sample mean

Describe the circumstances where the distribution of sample means is normal

• Population data is normal

• Sample size is 30

What is the goal of a hypothesis test?

Intends to understand how rare the results of something are

State the symbols and definition of the two types of hypotheses

• The null hypothesis, H₀, is the hypothesis of no difference

• The alternative hypothesis, H₁, is the hypothesis of difference

Alpha level

• The probability we’re comfortable saying is unlikely enough for us to determine a difference

• Typically 0.05, or 5%

• The higher the alpha level, the greater the chance there is that you reject the null hypothesis

Type I error

• reject a null hypothesis that is true

• Risk of a Type I error is the alpha level

Type II error

• fails to reject a null hypothesis that is false

• Risk of a Type II error is Beta (β)

Describe how the results of a hypothesis test with a z-score test statistic are reported in the literature

• “Consuming caffeine was shown to have a significant effect on sleep latency, z = 2.35, p<.05”

• Shows that the z score was used

• Shows that the test statistic fell within the critical region

Explain how the outcome of a hypothesis test is influenced by the sample size, the standard deviation, and the difference between the sample mean and the hypothesized population mean.

• Larger standard deviation makes it less likely to find statistically significant values

• Larger sample sizes make it more liekly to find statistically significant values

• The larger the difference between sample and population mean makes it more likely to find statistically significant values

Describe the assumptions underlying a hypothesis test with a z-score test statistic

• Random sampling: ensures a representative population

• Independent observations: observations do not influence each other

• Consistency of standard deviation: unaffected by treatment

• Normal distribution of sample means

Hypothesis of Direction

i.e., greater than or less than

Explain why it is necessary to report a measure of effect size in addition to the outcome of a hypothesis test.

Because statistical significance is not equal to practical significance

Formula for Cohen’s d

Guidelines for Cohen’s d

• .2 = small effect

• .5 = medium effect

• .8 = large effect

Explain how measures of effect size such as Cohen’s d are influenced by the sample size and the standard deviation

• Sample size does not influence Cohen’s d

• The larger the standard deviation, the less the practical effect size is

When are t-statistics used?

when there is not access to the mean population and standard deviation

T-statistic formula

Explain the relationship between the t distribution and the normal distribution

• T distribution estimates the normal distribution

• The greater the sample size, the more t will represent z

Explain how the likelihood of rejecting the null hypothesis for a t. test is influenced by sample size and sample variance

• A larger sample size increases the likelihood of rejecting the null hypothesis

• A larger sample variance decreases the likelihood of rejecting the null hypothesis