functions
3.0(2)
3.0(2)
Card Sorting
1/36
Earn XP
Description and Tags
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
37 Terms
1
New cards
function
* a rule that assigns every x-value to exactly one y-value
* passes “vertical line test”
* passes “vertical line test”
2
New cards
domain
* all possible x-values
* input, dependent variable
* use interval notation
* input, dependent variable
* use interval notation
3
New cards
range
* all possible y-values
* output, dependent variable
* use interval notation
* output, dependent variable
* use interval notation
4
New cards
continuity
* no breaks in the graph
* a “continuous” curve
* a “continuous” curve
5
New cards
removable discontinuity
* the graph can be repaired by filling in a single point
* hole(s) in the graph
* hole(s) in the graph
6
New cards
jump discontinuity
* a break in the graph
* if you trace the graph, you would have to jump to the next point
* if you trace the graph, you would have to jump to the next point
7
New cards
infinite discontinuity
* two or more pieces of the graph approach positive or negative infinity
* there is a vertical asymptote
* there is a vertical asymptote
8
New cards
increasing interval
* as x goes up, y goes up
* positive slope
* use x-values for the interval
* positive slope
* use x-values for the interval
9
New cards
decreasing interval
* as x goes up, y goes down
* negative slope
* use x-values for the interval
* negative slope
* use x-values for the interval
10
New cards
constant interval
* as x goes up, y stays the same
* 0 slope
* use x-values for the interval
* 0 slope
* use x-values for the interval
11
New cards
relative/local maximum
* point where the graph changes from inc. to dec.
* could be more than one
* could be more than one
12
New cards
relative/local minimum
* point where the graph changes from dec. to inc.
* could be more than one
* could be more than one
13
New cards
absolute maximum
* highest point on the graph
* only one
* if positive or negative infinity, none
* only one
* if positive or negative infinity, none
14
New cards
absolute minimum
* lowest point on the graph
* only one
* if pos. or neg. infinity, none
* only one
* if pos. or neg. infinity, none
15
New cards
vertical asymptote
* x=a is a va if f(x)→∞ or if f(x)→∞
* to find, set the denominator of a function’s equation equal to zero
* to find, set the denominator of a function’s equation equal to zero
16
New cards
horizontal asymptote
* y=b is a ha if f(x)→b as x→∞ or as x→-∞
* graphically, see where the ends of the graph go
* algebraically, if the degree of the denominator is greater than the degree of the numerator, ha: y=0
* if the degree of the denominator is less than the degree of the numerator, ha: none
* if the degrees are equal, y=quotient of leading coefficients
* the degree of a function is the highest exponent
* graphically, see where the ends of the graph go
* algebraically, if the degree of the denominator is greater than the degree of the numerator, ha: y=0
* if the degree of the denominator is less than the degree of the numerator, ha: none
* if the degrees are equal, y=quotient of leading coefficients
* the degree of a function is the highest exponent
17
New cards
end behavior
* the behavior at the left and right ends of the graph
* as x→-∞, what does y approach?
* as x→∞, what does y approach?
* right eb: approaches ∞
* left eb: approaches -∞
* as x→-∞, what does y approach?
* as x→∞, what does y approach?
* right eb: approaches ∞
* left eb: approaches -∞
18
New cards
bounded below
* there is some number b that is less than or equal to every number in the range
* have an absolute minimum
* have an absolute minimum
19
New cards
bounded above
* there is some number b that is greater than or equal to every number in the range
* have an absolute maximum
* have an absolute maximum
20
New cards
bounded
when the graph is bounded above and below
21
New cards
even functions
* y-axis symmetry
* for each point (x,y) on the graph, the point (-x,y) is on the graph
* f(-x)=f(x)
* all graphs with y-axis symmetry are even functions
* for each point (x,y) on the graph, the point (-x,y) is on the graph
* f(-x)=f(x)
* all graphs with y-axis symmetry are even functions
22
New cards
not functions
* for each point (x,y) on the graph, the point (x,-y) is on the graph
* all graphs with x-axis symmetry are not functions
* all graphs with x-axis symmetry are not functions
23
New cards
odd functions
* for each point (x,y) on the graph, the point (-x,-y) is on the graph
* f(x)=-f(x)
* all graphs with y-axis symmetry are odd functions
* f(x)=-f(x)
* all graphs with y-axis symmetry are odd functions
24
New cards
indentity/linear
f(x)=x
f(x)=x
\
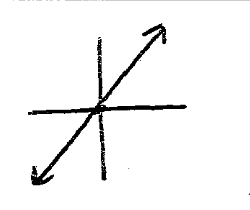
25
New cards
quadratic
f(x)=x^2
f(x)=x^2
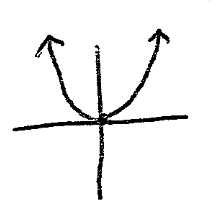
26
New cards
cubic
f(x)=x^3
f(x)=x^3
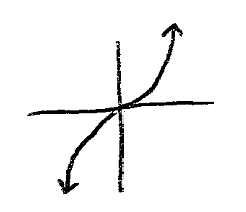
27
New cards
reciprocal
f(x)=1/x
f(x)=1/x
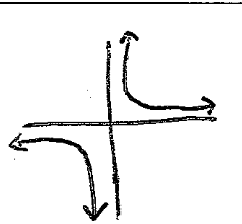
28
New cards
square root
f(x)=\\|x
f(x)=\\|x
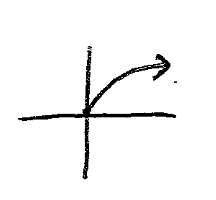
29
New cards
exponential
f(x)=e^x
f(x)=e^x
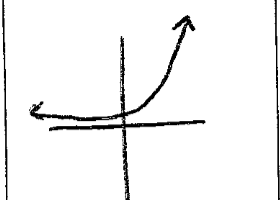
30
New cards
logarithmic
f(x)=lnx
f(x)=lnx

31
New cards
absolute value
f(x)=|x|
f(x)=|x|
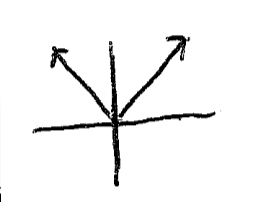
32
New cards
sine
f(x)=sinx
f(x)=sinx
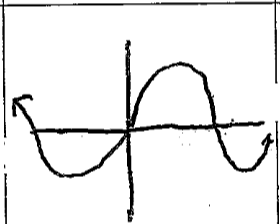
33
New cards
cosine
f(x)=cosx
f(x)=cosx

34
New cards
greatest integer
f(x)=\[x\]
f(x)=\[x\]
35
New cards
logistic
f(x)=1/1+e^-x
f(x)=1/1+e^-x

36
New cards
1/x^2

37
New cards
3\\|x
