Chapter 3a

tm slide 31

What is autocorrelation?

What is the “official” formula for first-order autocorrelation?

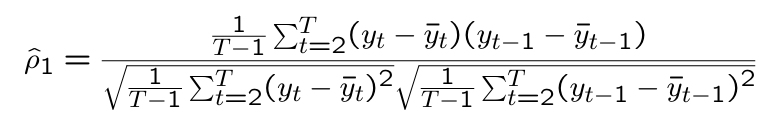
How is first-order autocorrelation usually computed?

In general, the k-th order autocorrelation can be estimated by …

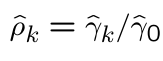
What does EAFC stand for?

empirical autocorrelation function

What does the empirical autocorrelation function refer to?

If we know the true functional form g() as well as the true parameter values theta, can we perectly predict the future value yT+1 based upon the past and present observations?

No, because of shocks

When is a time series considered white noise? Mathematical notation.

When is a time series considered white noise? In words.

Give a minimum requirement for a time series model g() to qualify as adequate.

The residuals ( estimated shocks ) have the white noise properties (A), (B), and (C)

How is the information set at time t-1 denoted?

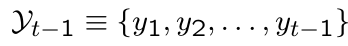
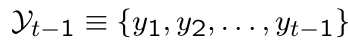
What is the information set at time t-1?

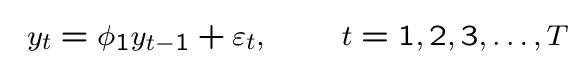
What is this model called?

AR1, first order autoregressive model

What does a first order autoregressive model look like?

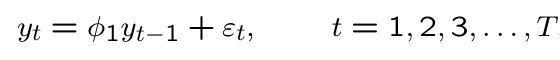
What can we conclude from this recursive substitution?

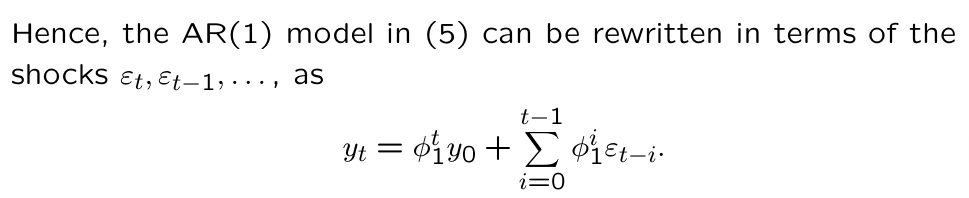
When | phi_1 | < 1. what do we say about the effect shocks have on future y’s?

Transitory effect

When | phi_1 | > 1. what do we say about the effect shocks have on future y’s?

Explosive effect

When | phi_1 | = 1. what do we say about the effect shocks have on future y’s?

Permanent effect

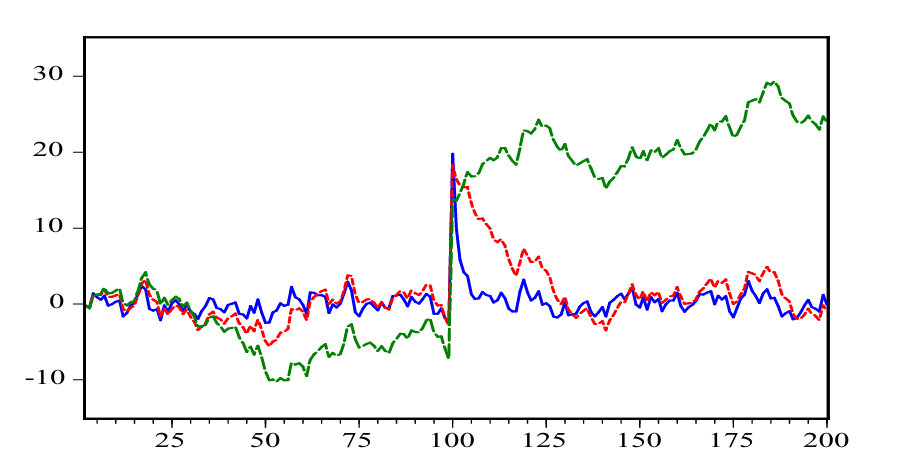
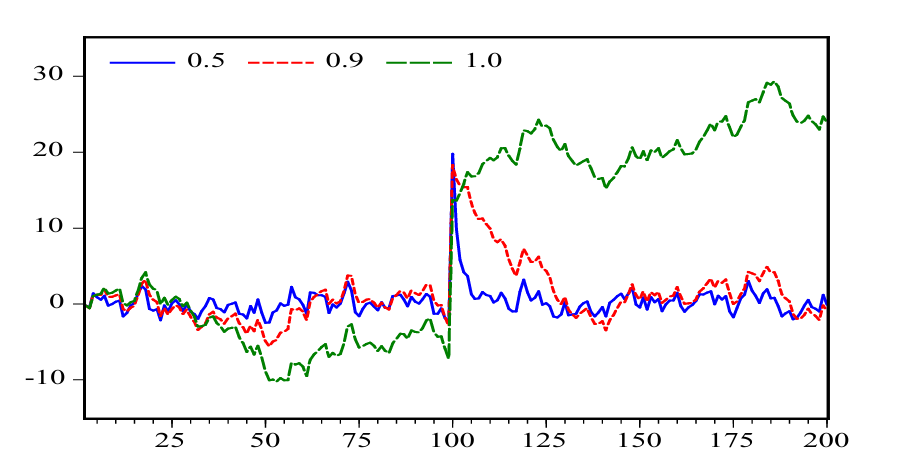
Which model has the highest phi and which on the lowest?

How to compute the unconditional mean with the quick and dirty approach?

In practice, time series often have an unconditional mean different from zero. How to account for this?

By including an intercept delta in the model

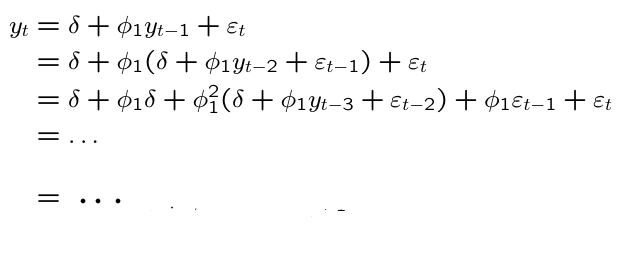
What does recursive substitution give us in an AR(1) model including an intercept?

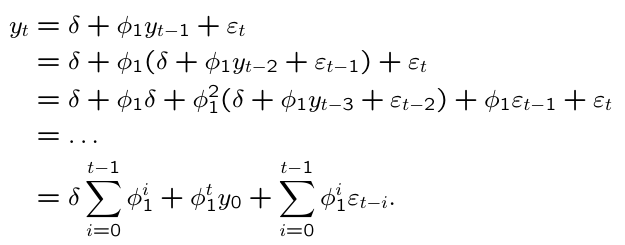
What is the unconditional mean for y_t in an AR(1) model including an intercept for t goes to infinity?

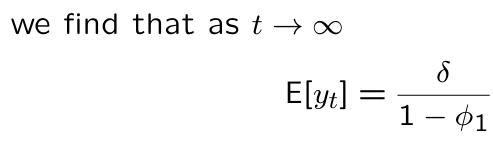
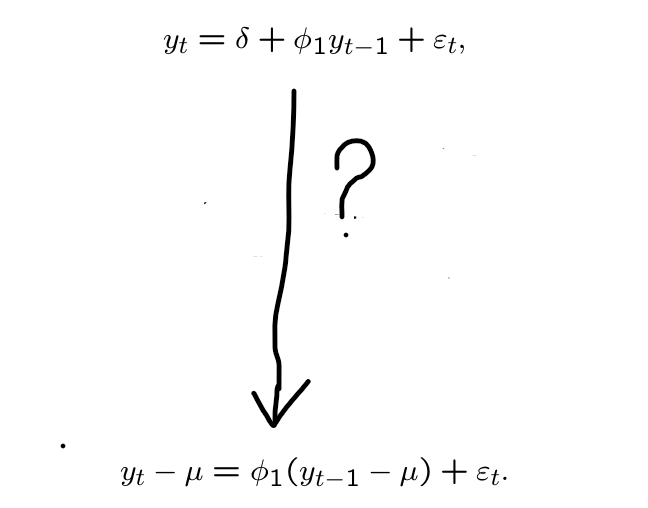
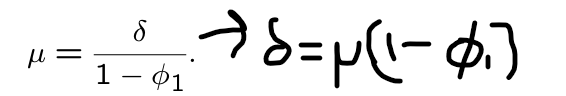
If the effect of the shocks is temporary, we call the AR(1) model …

stationary

What does it mean if a model is stationary?

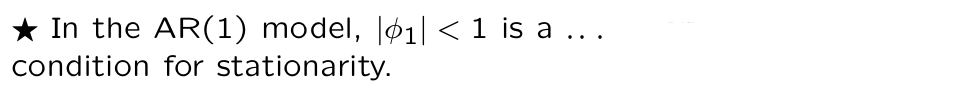
necessary and sufficient

Write gamma_k, the k’th order autocovariance of y_t, down in terms of expectations.

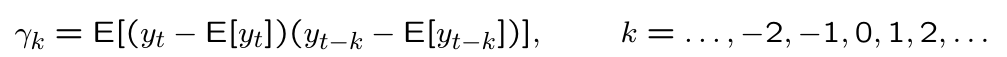
What can you say about the autocorrelation rho_0 and rho_minusk?

What do we do first when we want to calculate the ACF?

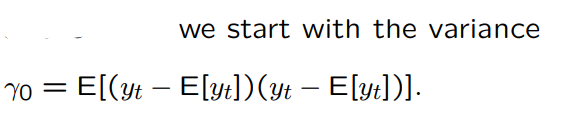
What is gamma_0 in the AR(1) model?

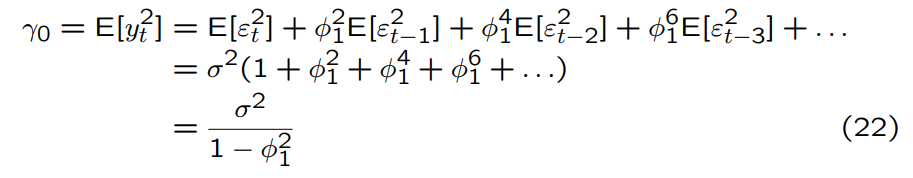
The larger the absolute value of phi1, the … gamma0 becomes relative to the conditional variance of y_t.

larger

What is the first order autocovariance for an AR(1) series?

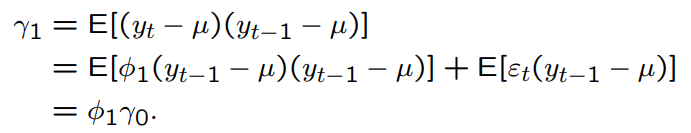
What is the first order autocorrelation for an AR(1) series?

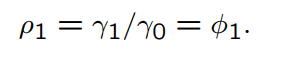
What is the formula for the kth autocorrelation of an AR(1) model?

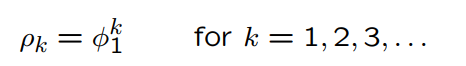
What is gamma_0 if phi = 1 in the AR(1) model?

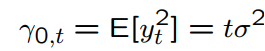
What is rho_k for phi =1 in the AR(1) model?

for any k > 0

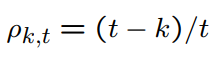
What happens to the theoretical autocorrelation in the AR(1) model with phi = 1 when t becomes large?

They all become equal to 1

Explain why the AR(1) model is insufficient.

How is the lag operator L defined?

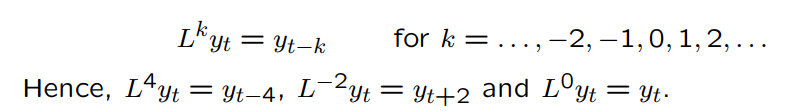
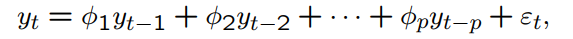
What is this model called?

AR(p)

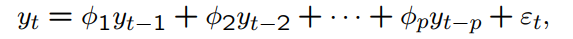
What is a more compact notation for the AR(p) model?

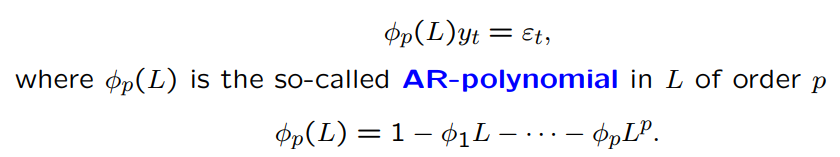
What is the AR polynomial in L of order p?

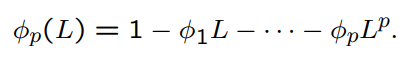
What is the characteristic polynomial?

What do the roots of the characteristic polynomial determine?

These roots determine whether the effects of shocks are transitory or permanent.

What is the characteristic polynomial of the AR(1) model?

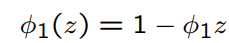
What is the root of the characteristic polynomial of the AR(1) model?

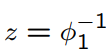
How to obtain an MA(q) model from an AR model?

What are the autocovariances for an MA(q) model?

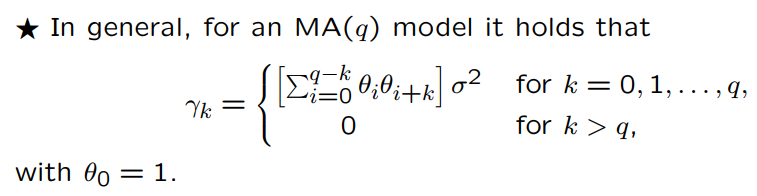
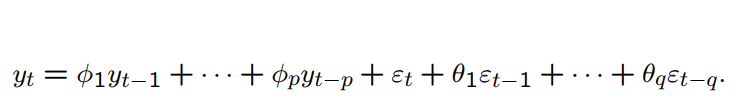
What is this model called?

an autoregressive moving average model of order (p, q) or, briefly, ARMA(p, q)

What is theta_q(L)?

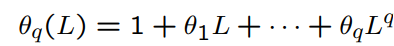
What is the compact notation for the ARMA(p,q) model?

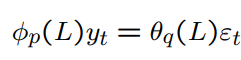
How to write the ARMA(p,q) model as a pure AR model?

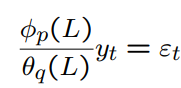
How to write the ARMA(p,q) model as a pure MA model?

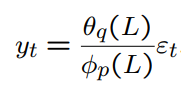
If yt is generated according to the AR(1) model, it is correlated with all its lagged values. Nevertheless, to describe the dynamic behavior of yt, it is sufficient to consider only the first lag yt−1. Does this hold more generally?

Yes, a nonzero k-th order autocorrelation does not necessarily imply that we need to include yt−k in a time series model for yt.

What does the kth order partial autocorrelation measure?

The dependence or correlation between yt and yt−k , after their common dependence on the intermediate observations yt−1, . . . , yt−k+1 has been removed.

How can the kth order partial autocorrelation be obtained?

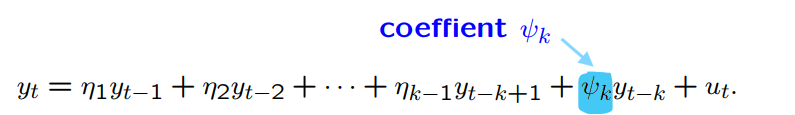
What can you say about the kth order partial autocorrelation for an AR model versus as MA model?

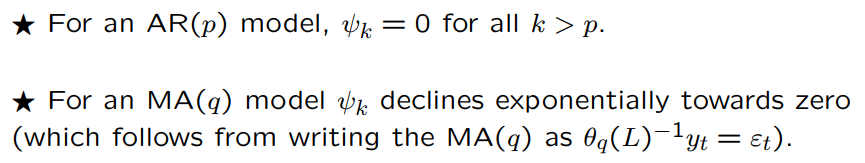
How can we characterize a time series when looking at the autocorrelations and partial autocorrelations?

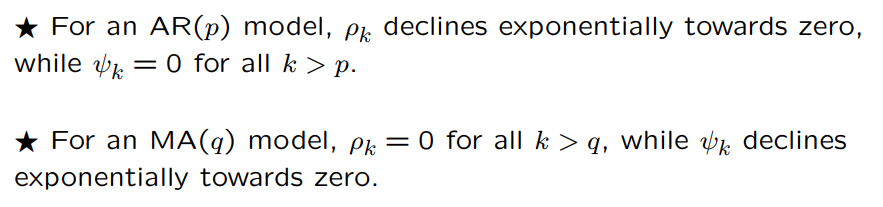
For a data set, ACF declines exponentially towards zero. The first three partial autocorrelations are significantly different from zero. What kind of model does this suggest?

AR(3) model