Continuous variables for multiple categorical variables with two or more groups

CONTINUOUS VARIABLES FOR MULTIPLE CATEGORICAL VARIABLES WITH TWO OR MORE GROUPS

What does a factorial ANOVA test? (aov(), then summary())

Full name: analysis of variance

A factorial ANOVA tests the effects of two or more categorical independent variables on a continuous dependent variable. It evaluates:

• Main effects of each factor

• Interaction effects between factors

What are the null and alternative hypotheses for a factorial ANOVA? (two-way ANOVA??)

Multiple sets of null and alternative hypotheses:

• Main effect of predictor A:

  • H₀: all group means of A are equal

    • the population means are the same for all groups of predictor A

  • H₁: at least one group mean differs

    • the population means are not the same for all groups predictor A

• Main effect of predictor B:

  • H₀: all group means of B are equal

    • the population means are the same for all groups of predictor B

  • H₁: at least one group mean differs

    • the population means are not the same for all groups predictor B

• Interaction between predictor A and predictor B: (A*B????)

  • H₀: the effect of A is the same at all levels of B

    • the population means for predictor A are the same for all groups of predictor B

  • H₁: the effect of A differs depending on the level of B

    • the population means for predictor A are not the same for all groups predictor B

**Make sure you know what main effects and interaction effects look like in a graph (see Section 16.2 of the book)

What do you do after a significant main or interaction effect in ANOVA?

Use post-hoc tests to determine which groups are significantly different from each other:

• Pairwise comparisons (TukeyHSD() or posthocPairwiseT())

• Planned comparisons for contrasts of a prior interest:

*Adjust p-values for multiple comparisons using a Bonferroni correction: 𝑝′ = 𝑝*𝑚

• 𝑚 = the total number of comparisons

What is the test statistic and how are degrees of freedom calculated in factorial ANOVA?

Test statistic: F

• higher values correspond to a lower probability of H0 being true for a model term

Degrees of freedom:

• Factor A: R−1

  • R is the number of groups for predictor A

• Factor B: C−1

  • where C is the number of groups for predictor B

• Interaction A and B: (R−1)(C−1)

• Residuals: N − (R*C)

  • N is the total number of observations

*exact rejection regions depend on degrees of freedom

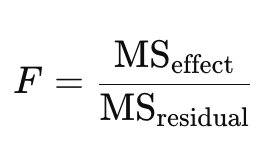
What is the relationship between sums of squares (SS), means of squares (MS), and the F-statistic in ANOVA?

• Sums of Squares (SS) measure the total variability:

  • SSbetween​: variability between group means

  • SSwithin (residual): variability within groups

• Mean Squares (MS) are averages of sums of squares: MS = SS / df​

• F-statistic is the ratio of these mean squares: F = MSbetween / MSwithin​​

A higher F-value suggests that between-group differences are large relative to within-group variation, which may indicate a significant effect.

What is partial eta squared, and how is it interpreted? (etaSquared()) - Effect size

Partial η² measures the proportion of variance explained by one factor or interaction while controlling for others (0-1): Apply to both main effects and interaction effects.

• 0.01 = small

• 0.06 = medium

• 0.14 = large

*larger values correspond to more unequal means

• Partial η² measures the effect size of individual model terms (main effects or interactions), controlling for other terms in the model

What are the assumptions of factorial ANOVA?

• Residuals are normally distributed

  • Check with: Shapiro-Wilk test (shapiro.test()), histogram, QQ plot

• Homogeneity of variance: The variance is the same in both groups

  • Check with: leveneTest()

• Residuals are independent