Study Guide Chapter 21 !!

Budget Constraint

A budget constraint represents all the combinations of goods and services for a buyer on a budget.

It helps illustrate trade-offs — if you spend more on one good, you have less to spend on another.

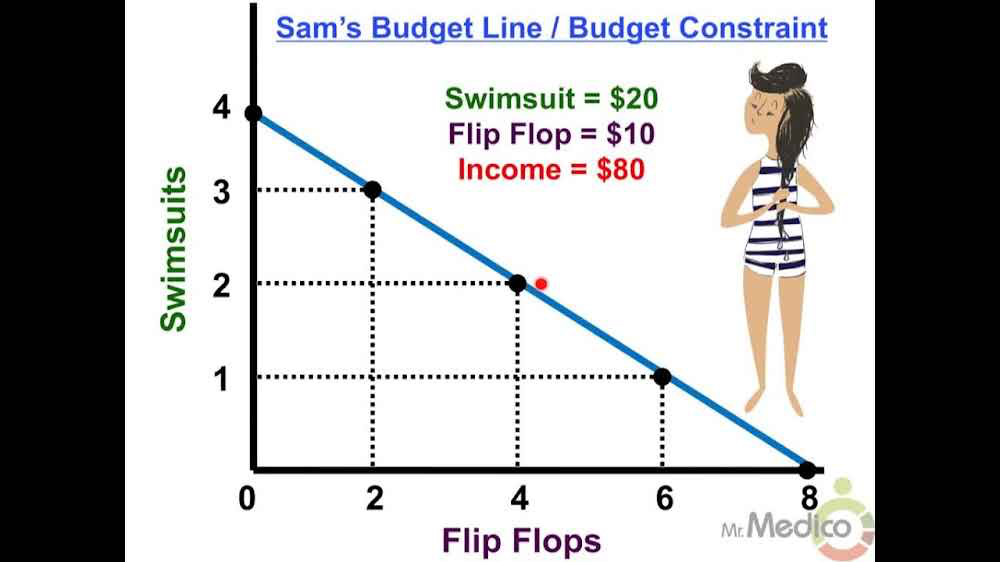
How would a budget constraint be impacted by the following?

An increase in income

The budget constraint shifts outward (to the right)

• The consumer can now afford more of both goods.

How would a budget constraint be impacted by the following?

If the price of one of the goods increased

The budget constraint pivots inward on the axis of that good

• The consumer can now afford less of that good.

How would a budget constraint be impacted by the following?

If the prices of both goods decreased by 10%

The budget constraint shifts outward (away from the origin)

• Since both goods are cheaper, the consumer can afford more of both, even with the same income.

The Indifference curve

represents all the combinations of two goods that give a consumer the same level of satisfaction or utility — meaning, the consumer is indifferent between them.

Indiffernece curve properties

1. Higher curves are preferred

| More of both goods = more happiness

2. Curves slope downward

| Trade-offs: more of one = less of the other

3. Curves do not cross

| Preferences are consistent — no overlap

4. Curves are bowed inward

| Diminishing marginal utility — variety is better

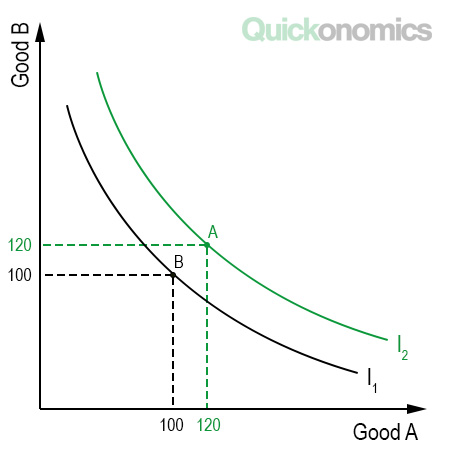
What is the most preferred point? Why?

Point A is the most preferred because it lies on the highest indifference curve (I₃).
📈 A higher indifference curve means a higher level of utility (more satisfaction), so the consumer prefers bundles on I₃ over those on I₂ or I₁.

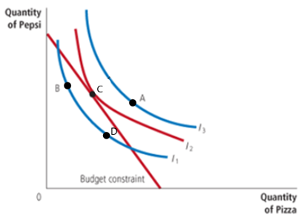
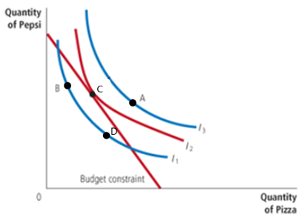
b. Why would this person be equally happy at points B and D?

✅ Points B and D lie on the same indifference curve (I₁).
🙂 Since all combinations on a single indifference curve provide the same level of satisfaction, the consumer is indifferent between them.

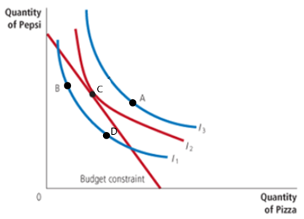
c. What is the optimal consumption point? Why?

✅ Point C is the optimal consumption point because it is where the budget constraint touches the highest possible indifference curve (I₂).
🎯 This is the best affordable option — it maximizes utility while staying within the budget.