Ch. 14 (Game Theory)

In an oligopoly, all firms worry not just about the quantity they produce, but also about how other firms produce, making this a strategic situation.

We will use game theory to analyze oligopolies.

game theory definition:

the economic study of how agents interact in strategic situations.

• ex: oligopoly, warfare, chess, strategical communication, etc.

3 things a game consists of:

players, strategies, and payoffs

ex: firm competition applying to games. list the players, strategies, and payoffs.

• suppose we have two firms competing in an oligopoly —> the two firms are the players in that game.

• suppose those firms are choosing how much to produce and how much firms produce jointly produces a price in the marketplace. What options do the firms have in this game? —> quantities that firms choose to produce.

• what are the payoffs of firms? —> profit

key note about players in a game!

there needs to be multiple players. This is b/c while you can apply game-theoretical tools to one firm, it would just be a decision (the strategy part is interacting with other players).

key note about strategies!

a strategy is a complete, contingent plan of action. Payoffs depend on all players’ strategies. This is more complicated than just the choices someone has. In this class, we can think of strategies as being the same as actions.

• ex: in chess, it would be when you have a plan for every single location on the chess board that you could end up in. it is very complicated.

key note about payoffs in a game!

the outcome of a game that is typically represented by “utility” (how happy someone is). Higher numbers are more preferred.

look at the example of firm competition game in chapter 13 notes!

please

note some key traits of this example.

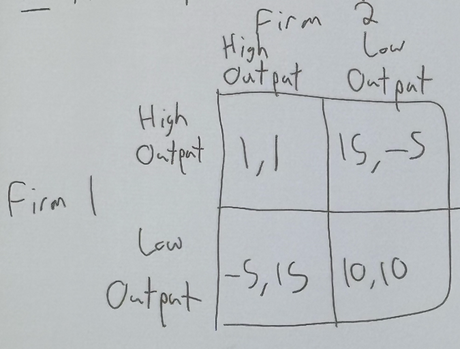
• the row player is always the first payoff number in a cell

• the column player is the second payoff number in a cell

• this is called the matrix/strategic form, where players simultaneously choose strategies

dominant strategy defintion:

a strategy that yields the best outcome for a player regardless of what others do

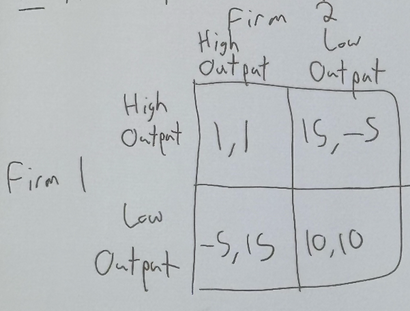
dominant strategy applied here?

A firm in this case would always prefer to select high output b/c in this case, “high” is the dominant strategy for each firm. This is b/c it gives the highest utility regardless of what others do (always preferred).

key note about dominant strategies!

dominant strategies do NOT guarantee the best overall outcome in the game.

Nash equilibrium definition:

a strategy for each player that, given what others are doing, a player cannot deviate and do better. a Nash equilibrium is where both players choose the best response to what the others are doing. IT IS A STABLE POINT IN THE GAME.

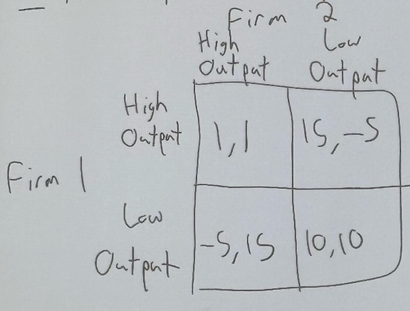
what is the Nash equilibrium in this game?

it is for both firms to produce high output (high, high). it cannot be (low, low) since a firm deviates to “high” when the other firm plays “low”.

Prisoner’s Dilemma. you and your partner rob a bank and are caught. You are placed in separate rooms, and you can either confess or stay silent. If both of you stay silent, each gets 1 year in jail. If you both confess, each gets 10 years in jail. If one person confesses and the other stays silent, the person confessing gets 0 years in jail and the silent person gets 20 years in jail. what is the matrix form of this?

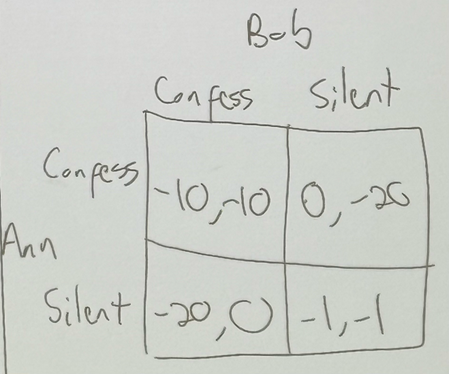
the players are the two people (Ann & Bob).

the strategies are you can either confess or stay silent.

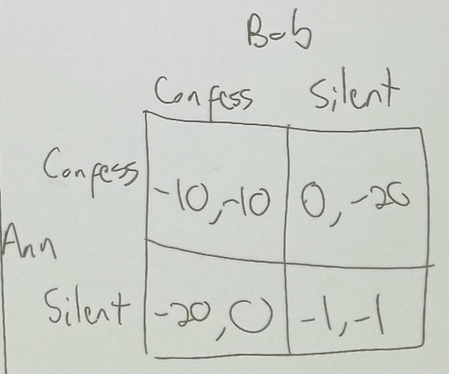
are there dominant strategies?

in both cases (Ana and Bob), confessing is better. Confessing for either player is a dominant strategy.

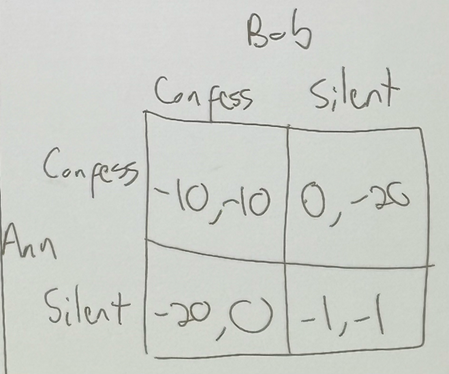
what are all the Nash equilibrium in the game?

both players confessing is a Nash equilibrium.

• oligopoly firm competition is a prisoner’s dilemma. the Nash equilibrium yields a worse overall outcome than a different possible outcome of the game (silent, silent). that is a dominant strategy, not a Nash equilibrium.

note!

if a dominant strategy exists in a game, it MUST be used in a Nash equilibrium. It is a strategy that you never want to deviate from. however, a Nash equilibrium existing does NOT mean those strategies are dominant.

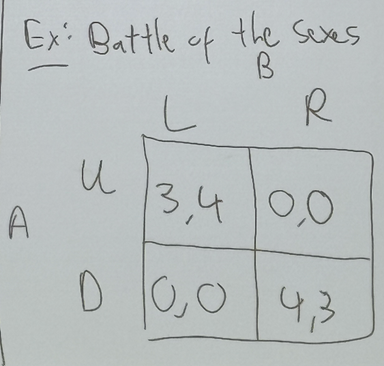
battle of the sexes example

• dominant strategy: there is not a dominant strategy since no strategy does best regardless of what others do.

• Nash equilibrium: (up, left) and (down, right). both are Nash equilibrium b/c if you know what the other person is doing at that point, you would not want to deviate from the choice you are at, as you will end up with 0.

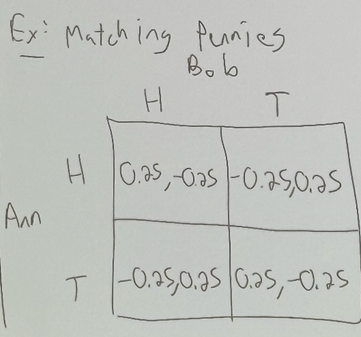
matching pennies example: both players take a quarter and privately choose a side simultaneously. Ann wins both if they match. Bob wins both if they mismatch.

• dominant strategy: there is not a dominant strategy.

• Nash equilibrium: there is no Nash equilibrium b/c if one person wins, the other person loses, which means they would want to switch their strategy so they wouldn’t lose. —> this applies in “pure strategies”

note: a “mixed” strategy randomly decides between pure strategies.

• a Nash equilibrium exists in the matching pennies example in mixed strategies

• in this class, we only have to consider pure strategies, not mixed strategies

zero-sum bar definition

a game in which the gains of one player come from the losses of other players (also sometimes called a constant-sum game). the sum of any payoffs is zero or the sums of any payoff are constant. there is nothing destroyed or net gained by playing the game.

• ex: poker, any sport with a winner and a loser, chess, rock-paper-scissors

negative-sum game definition

a game in which players as a group receive bad payoffs as a collective by playing the game. resources are typically destroyed.

• ex: trade wars, warfare, tariffs, riots

positive-sum game definition

a game in which players receive collectively positive payoffs by playing the game. resources are typically created.

• ex: TPSs, trade and exchange in general

tree form game definition

a tree form game is a game form that reflects a sequential game.

• a game tree consists of a root (player node), decisions (actions) represented by branches, player nodes where players make decisions, and terminal nodes (payoffs) that end the game.

• you start at the root, a person makes a decision that goes along branches, etc., etc., and then you eventually arrive at the terminal node that ends the game.

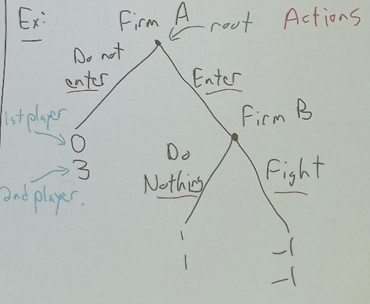
game tree example

• the first payoff will always be the payoff of player 1. the second number will always belong to the second player, sequential.

• the branches are represented by the decisions they can enter down.

the prediction method will generally use for tree form games is called ___.

backward induction

backward induction definition

starting at the last nodes in the game tree, denote what decision that player would make if they were maximizing their payoff at that node. then, we repeat this process going backwards until the root of the game has been reached.

really important note!

backward induction equilibrium and Nash equilibrium give DIFFERENT predictions. every backward induction equilibrium IS a Nash equilibrium as you play each move as your best move. NOT every Nash equilibrium is a backward induction equilibrium.

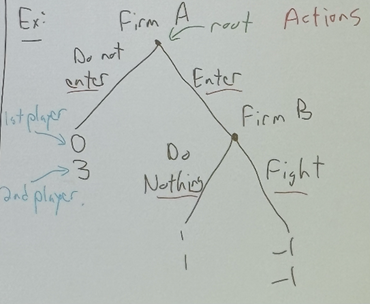
claim:

in this example, “not enter” for Firm A and “fight” for Firm B (not enter, fight) is a Nash equilibrium. this is not a backward induction equilibrium (Firm B would never choose “fight” over “doing nothing” as they would get -1 instead of 1).

• “fighting” when other firms enter a market is what firms like Walmart do to prevent competition. this is called predatory pricing.

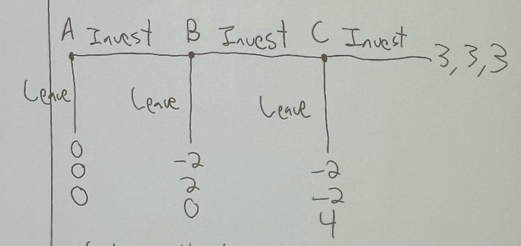
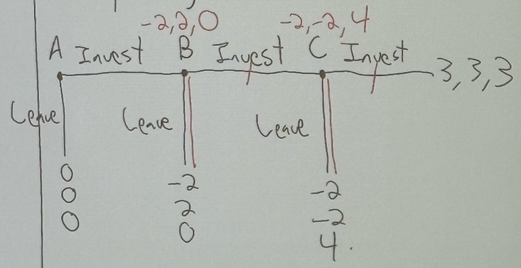
what is the backward induction equilibrium?

(leave, leave, leave)

tit-for-tat definition (the strategy in Robert Axelrod’s tournament that had the highest average payoff against other strategies)

• in period 1, I am going to cooperate. In any future/subsequent period, I will play what the other player played in the previous period.

  • This says that if you are against someone who likes cooperating, this will cause high levels of cooperation. If someone is more selfish, then they don’t allow to be defected more than once. Built into this strategy is the idea of forgiveness. If both are defective, the one party can decide they’d like to go back to cooperating, and the other party goes back to cooperating as well.

• Firms in an oligopoly may be able to collude in a long-run setting.