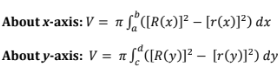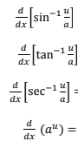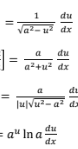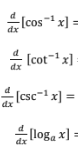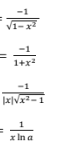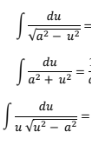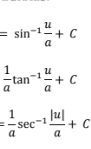AP Calc AB - AP calc memorization flash cards

Limit definition of a derivative

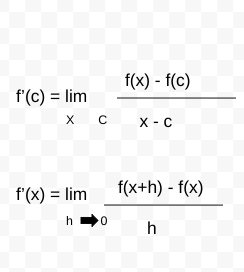
Intermediate Value Theorem (IVT)

If the function f(x) is continious on [a,b] and y is a number between f(a) and f(b) then there exists at least one number x = c in the open interval (a,b) such that f(c ) = y

Mean Value Theorem (MVT)

If the function f(x) is continuous on [a,b] AND the first derivative exists on the interval (a,b) then there is at least one number x = c in (a,b) such that f’(c ) = f(b) - f(a) / b - a

Rolle’s Theorem

If the function f(x) is continuous on [a,b] AND the first derivative exists on the interval (a,b) AND f(a) = f(b) then there is at least one number x = c in (a,b) such that f’(c ) = 0

Extreme Value Theorem

If the function f(x) is continuous on [a,b], then the function is guaranteed to have an absolute maximum and an absolute minimum on the interval.

d/dx (x^n)

nx^(n-1)

d/dx(sinx)

cos x

d/dx(cos x)

-sin(x)

d/dx(tanx)

sec²x

d/dx(cotx)

-csc²x

d/dx(sec x)

secx * tan x

d/dx (cscx)

-cscx * cotx

d/dx (ln u)

1/u * du/dx

d/dx(e^u)

e^u du/dx

chain rule

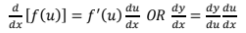
product rule

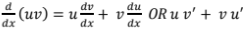
Quotient Rule

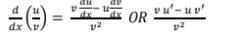
Derivative of an Inverse function

if f has an inverse function g then:

derivatives are reciprocal slopes

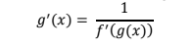
Implicit Differentiation

You will have dy/dx for each y in the original function or equation

1. Isolate the dy/dx

2. if taking second derivative d²y/dx², you will substitute expression you found for first derivative somewhere in the process

Average Rate of Change / AROC

f(b) - f(a) / b - a

Instantaneous Rate of Change / IROC

Curve Sketching an Analysis

y = f(x) must be continuous at each:

1. Critical Point: dy/dx = 0 or undefined

   1. LOOK OUT FOR ENDPOINTS

2. Local minimum

   1. dy/dx goes (- , 0, +) or (-, und, +) or d²y/dx²>0

3. Local Maximum

   1. dy/dx goes (+,0,-) or (+,und,-) or d²y/dx²<0

4. Point of Inflection: concavity changes

   1. d²y/dx² goes from (+,0,-), (-,0,+), (+,und,-) OR, (-,und+)

First Derivavtive

f’(x) > 0 function is increasing

f'(x) < 0 function is decreasing

f’(x) = 0 or DNE: Critical Values at x

Relative Maximum: f’(x) = 0 or DNE and sign of f’(x) changes from + to -

Relative Minimum: f’(x) = 0 or DNE and sign of f’(x) changes from - to +

Absolute Max or Min - MUST CHECK ENDPOINTS ALSO:

the maximum value is a y-value

Second Derivative

f’’(x) > 0 function is concave up

f’’(x) < 0 function is concave down

f’(x) = 0 and sign of f’’(x) changes, then there is a point of inflection at x

Relative Maximum: f’’(x) < 0

Relative Minimum: f’’(x) > 0

Write the equation of a tangent line at a point:

You need a slope (derivative) and a point

y₂ - y₁ = m(x₂-x₁)

Horizontal Asymptotes

ONLY FOUR THINGS THAT YOU CAN DO ON A CALCULATOR THAT NEEDS NO WORK SHOWN

1. Graphing a function within an arbitrary view window

2. finding the zeros of a function

3. computing the derivative of a function numerically

4. computing the definite integral of a function numerically

Distance, Velocity, and Acceleration

x(t) = position function

v(t) = velocity function

a(t) = acceleration function

Speed is |velocity|

Displacement

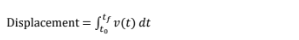
Total Distance

average velocity

accumulation

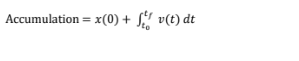
Logarithms Definitions

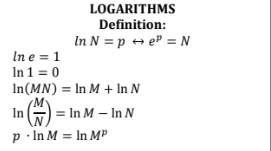
Exponential Growth and Decay

When Solving a differential equation:

1. seperate variables first

2. integrate

3. add +C to one side

4. Use initial conditions to find “C”

5. Write the equation in the form y = f(x)

Fundamental Theorem of Calculus

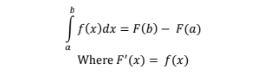
Corallary to FTC

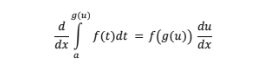
Average Value

If the function f(X) is continuous on [a,b] and the first derivative exists on the interval (a,b) then there exists a number x = c on (a,b) such that f_avg= 1/(b-a) int_a^b f(x)dx = int_a^bf(x)dx/b-a

This value f(c ) is the “average value” of the ifunction on the integral [a,b]

Riemann Sums

Sin(0) Cos(0) tan(0)

0, 1, 0

sin(pi/6), cos(pi/6), tan(pi/6)

1/2, sqrt(3)/2, sqrt(3)/3

sin(pi/4), cos(pi/4), tan(pi/4)

sqrt(2)/2, sqrt(2)/2, 1

sin(pi/3), cos(pi/3), tan(pi/3)

sqrt(3)/2, 1/2, sqrt(3)

sin(pi/2), cos(pi/2), tan(pi/2)

1, 0, infinite

sin(pi), cos(pi), tan(pi)

0, -1, 0

Area of cross section for squares

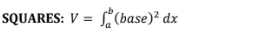
area between equilateral triangles

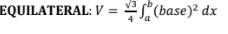
area between isosceles right triangles

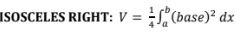
area between curves rectangles

area between semi-circles

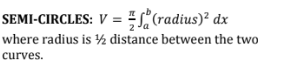
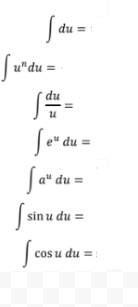
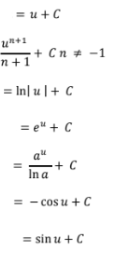
volume by washer method - about y and x axis

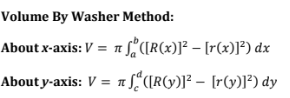
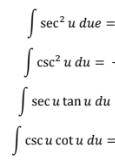
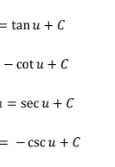
Area Between Two Curves

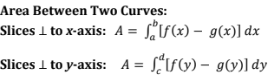
volume by disk method

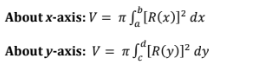
volume by washer method