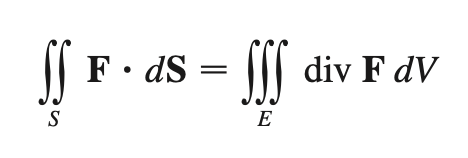Calc III - ultimate review

sphere eqn

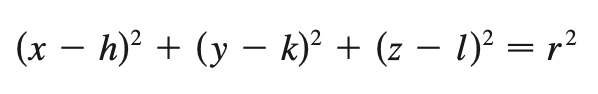
direction angles

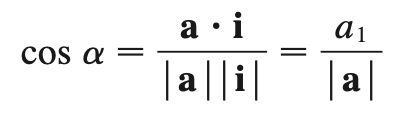
v = <a, b, c>

a → α

scalar projection (b onto a)

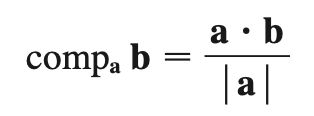
*magnitude of b that falls over a

vector projection (b onto a)

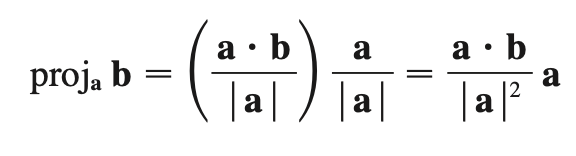
*captures scalar projection as well as direction

limit of a vector

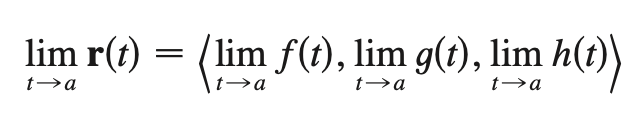
dot product

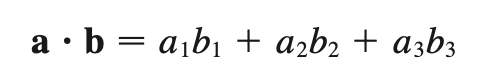
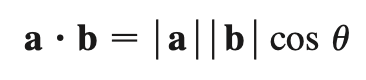
cross product

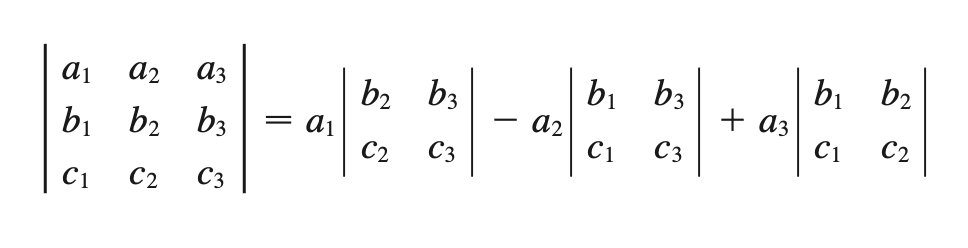
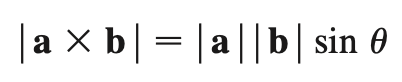
• a x b = area of parallelogram

• |a • (b x c)| = area of parallelepiped

vector eqn

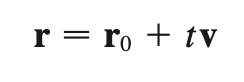
parametric eqns (vector)

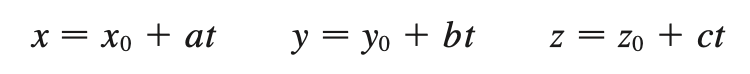
v = <a, b, c>

• v: parallel to actual vector, defines direction

symmetric eqns (vector)

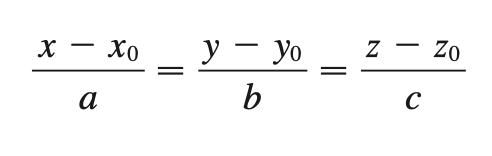
2-point vector eqn

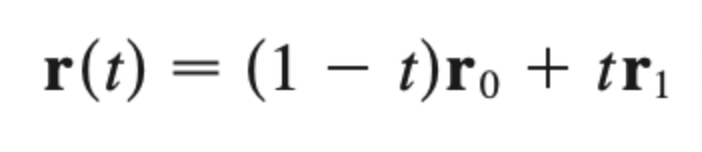
r₀ + v = r₁

• v: vector connecting points r₀ & r₁

scalar plane eqn

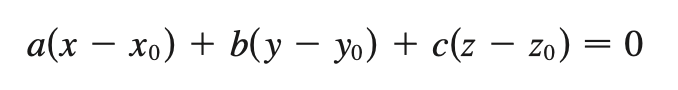
P₀ = <x₀, y₀, z₀>

n = <a, b, c>

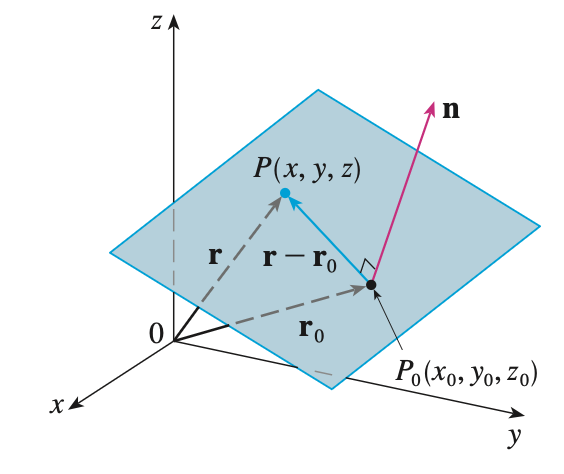
linear plane eqn

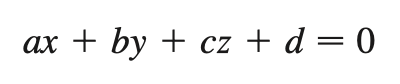
d = -(ax₀ + by₀ + cz₀)

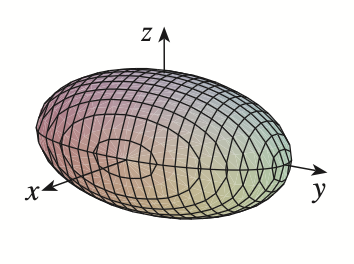
ellipsoid

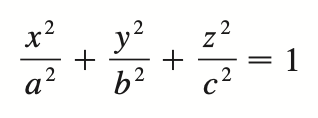
cone

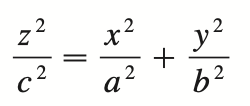
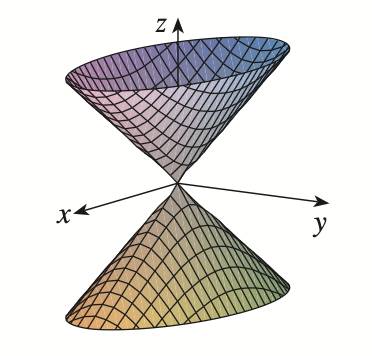
elliptic paraboloid

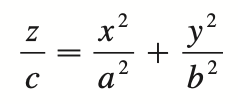
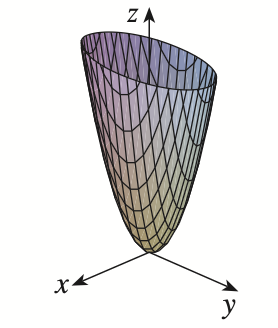
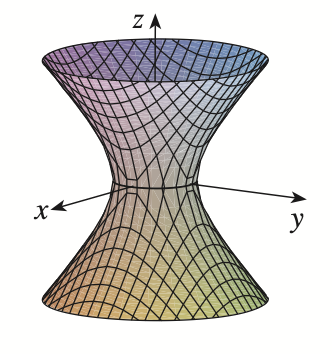
hyperbolic of one sheet

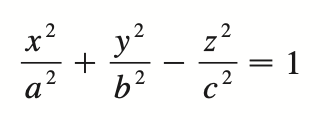
hyperbolic paraboloid

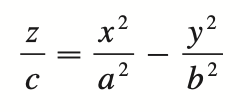
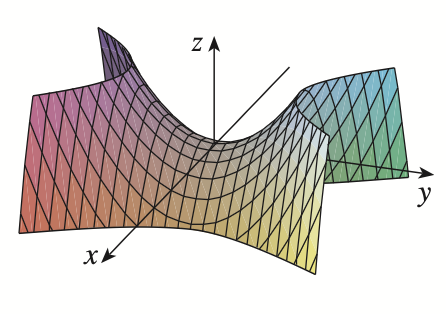
hyperboloid of two sheets

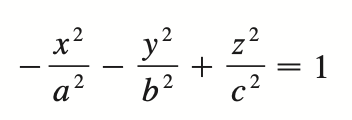
unit tangent vector

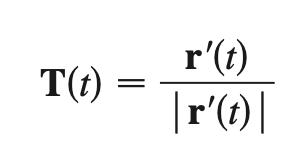
derivative of a vector

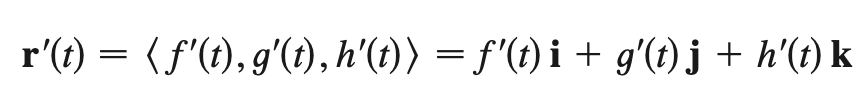
derivative of cross & dot product

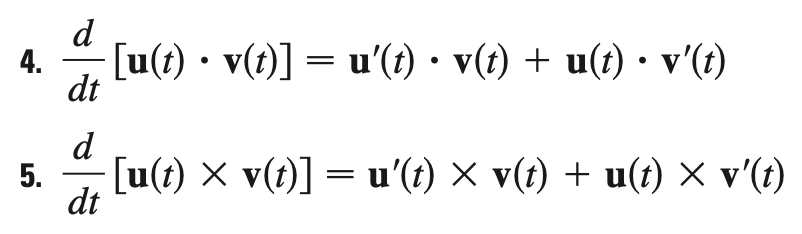
integral of a vector

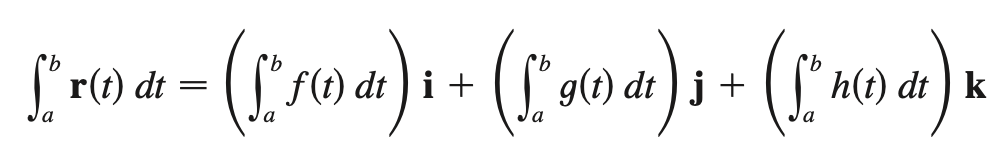
arc length

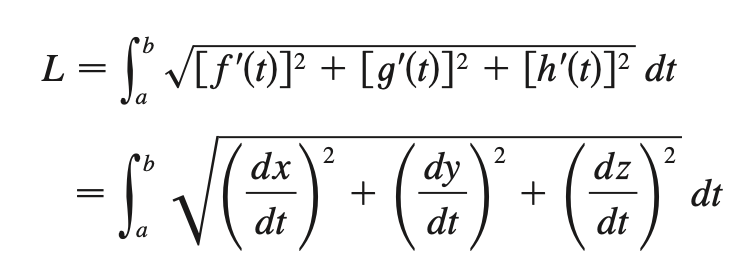
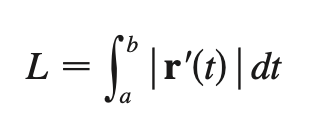
curvature

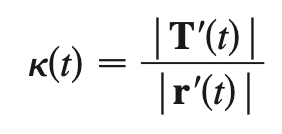
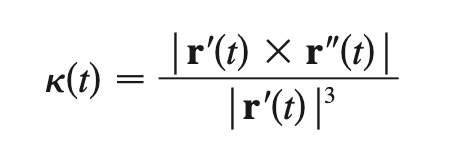
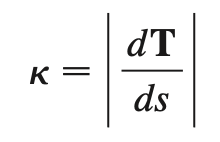
unit normal

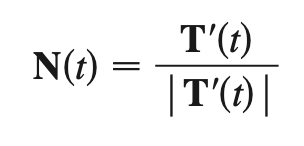
unit binormal

B(t) = T(t) x N(t)

acceleration (tangent & normal)

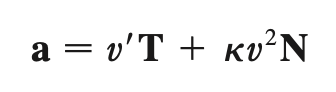
partial derivative

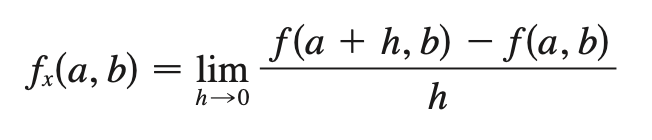
b = constant

derivative notation

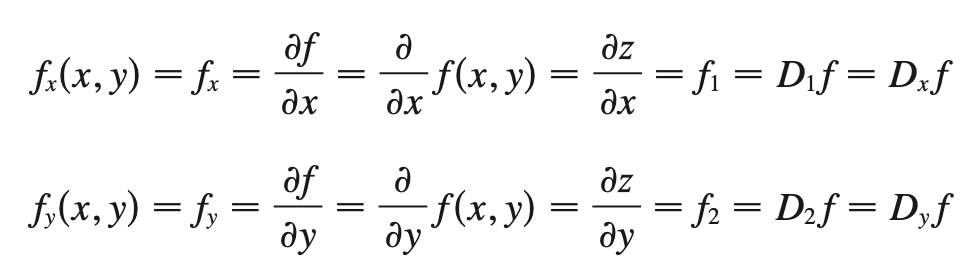
Clairaut’s thm

If f_xy & f_yx are continuous on D

• f_xy(a, b) = f_yx(a, b)

  • True for most functions

plane eqn

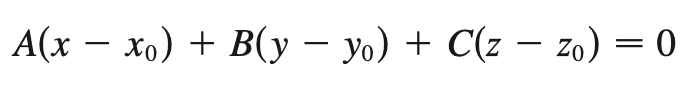
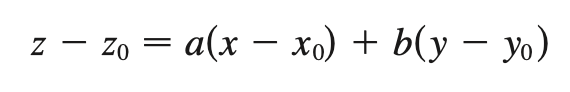
• a = -A/C

• b = -B/C

total differential

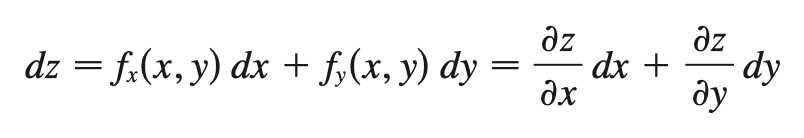
chain rule (multivariable)

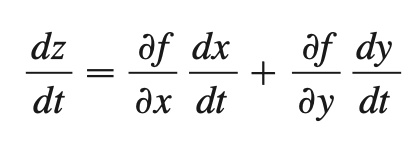
intermediate variables: ???

implicit differentiation??? (multivariable)

implicit function theorem?

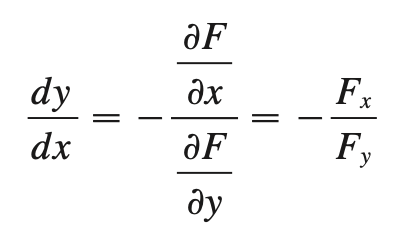
directional derivative

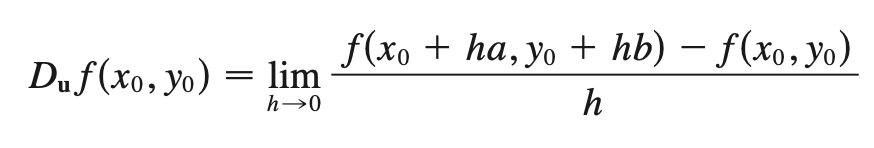
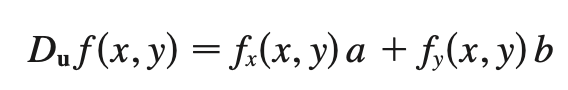
rate of change of a multivariable function along some unit vector u

• u = <a, b>

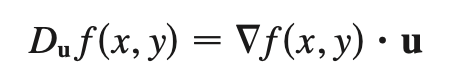
gradient vector

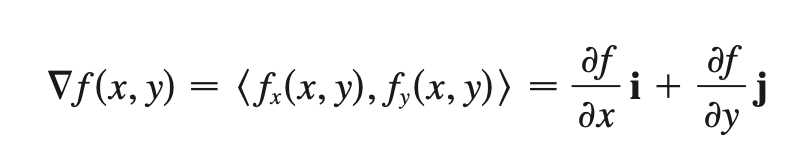
• shows direction of fastest increase

tangent plane (symmetric eqns)

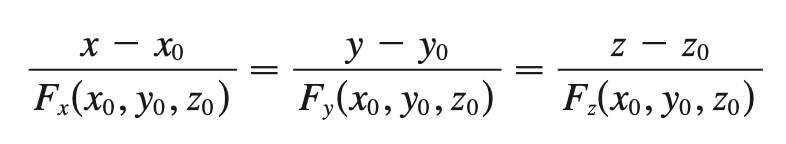
critical point (multivariable)

1. f_x and f_y = 0

2. f_x or f_y DNE

SDT

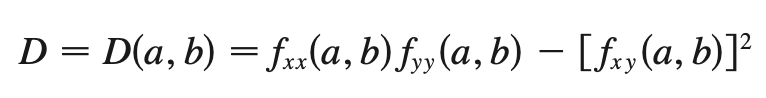
• D > 0:

  • f_xx(a, b) > 0

    • Local minimum

  • f_xx(a, b) < 0

    • Local maximum

• D < 0:

  • no max/min

EVT (multivariable)

if f is continuous on closed, bounded D:

• Both an absolute max & min exist within D

lagrange multiplier

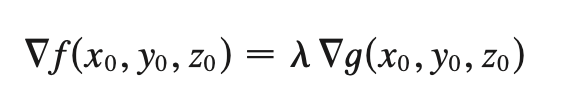
1. Find all values of lambda satisfying:

   • ∇f(x₀, y₀, z₀) = λ∇g(x₀, y₀, z₀)

   • g(x, y, z) = k

2. Evaluate f @ all points

3. Greatest f is maximum, smallest is minimum

average value (multivariable)

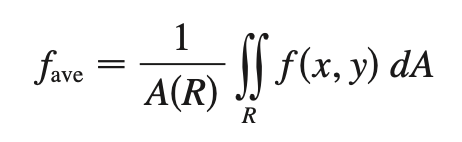
double integral

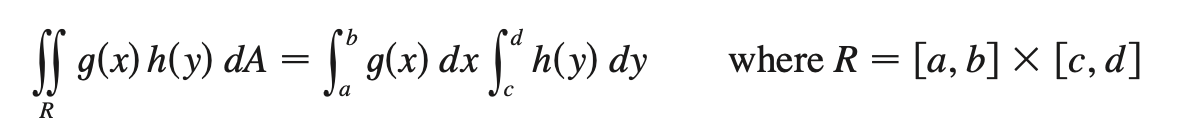
general regions (double integral)

• type 1: between 2 continuous functions of x

• type 2: between 2 continuous functions of y

double integral (polar)

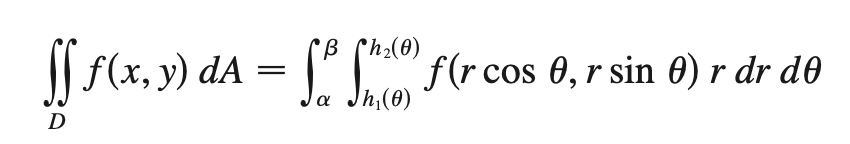
*similarity: r dθ = arc length → “area” dA = r dr dθ

lamina mass

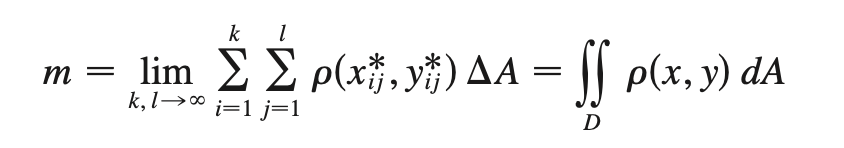
COM (multivariable)

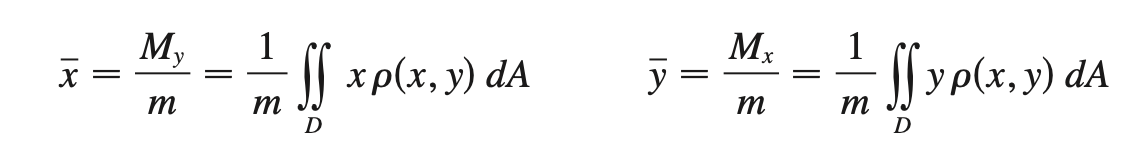
moment of inertia (I_x, I_y, I₀)

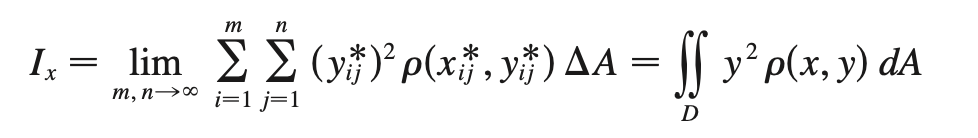
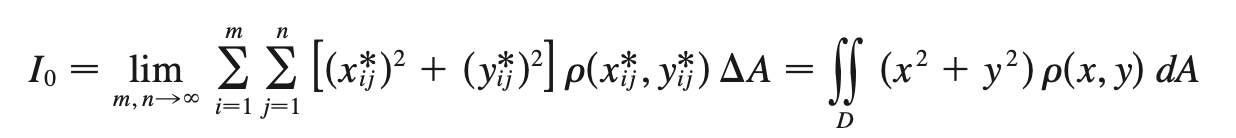
I₀ + I_x + I_y

radius of gyration

average distance from the axis of rotation (R)

• R = sqrt(I/m)

  • If all mass was concentrated R distance from the axis, I = mR² regardless of shape/distribution

surface area (multivariable)

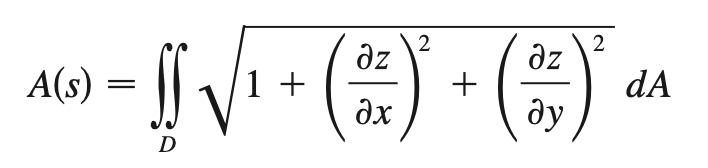
triple integral

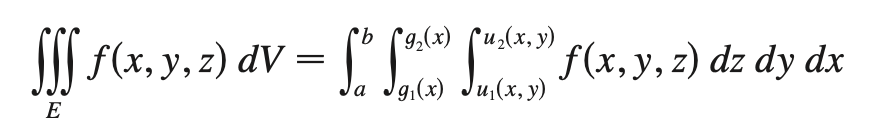
• yields bound volume if f(x, y, z) = 1

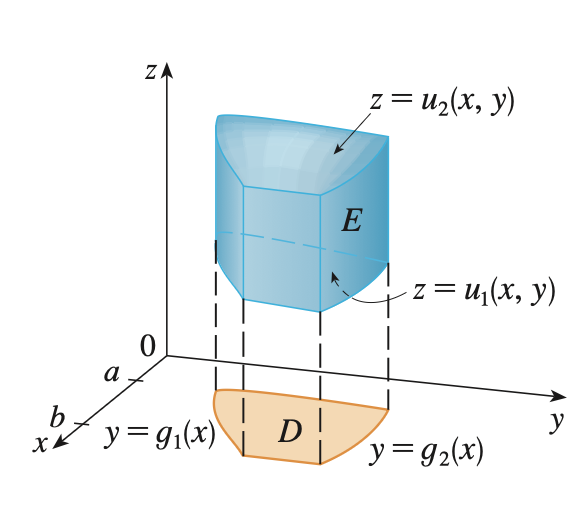
general regions (triple integral)

type 1:

• between graphs of 2 continuous f(x, y) functions

• region D projected from xy-plane

type 2:

• between graphs of 2 continuous f(y, z) functions

• region D projected from yz-plane

type 3:

• between graphs of 2 continuous f(x, z) functions

• region D projected from xz-plane

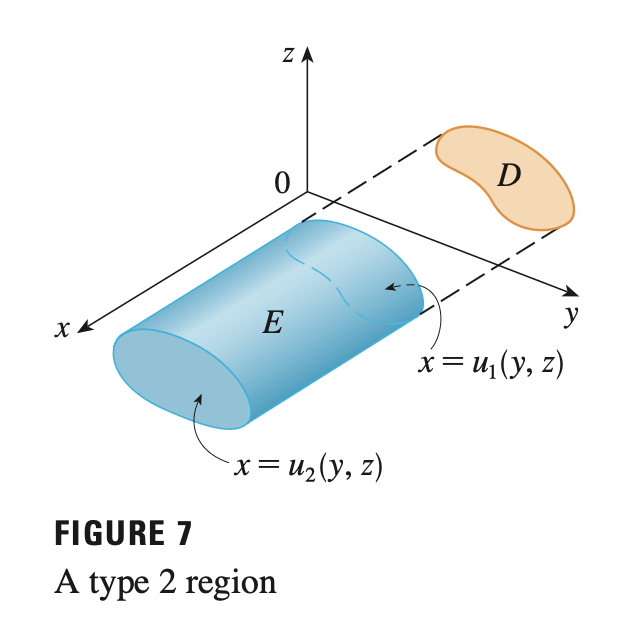
moments of inertia (3 axes)

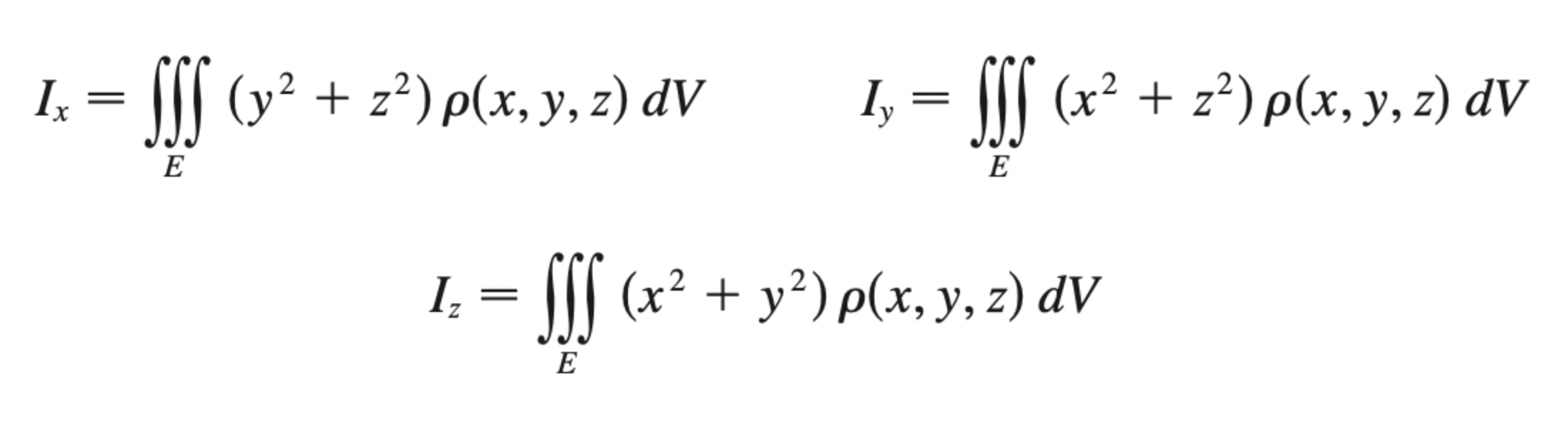
moments (3 axes)

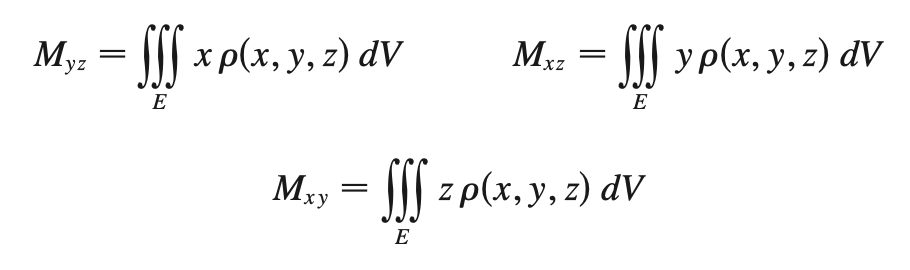
x̄ = M_yz/m

ȳ = M_xz/m

z̄ = M_xy/m

cylindrical coords

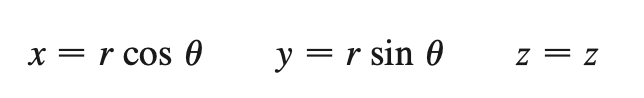
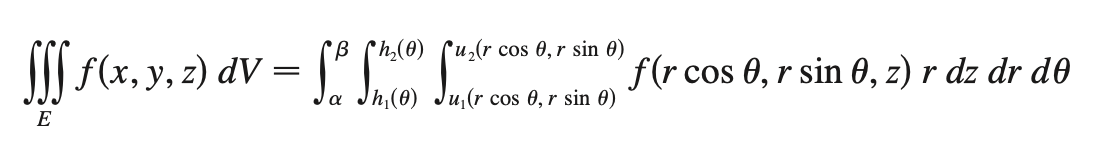
(θ, r, z)

spherical coords

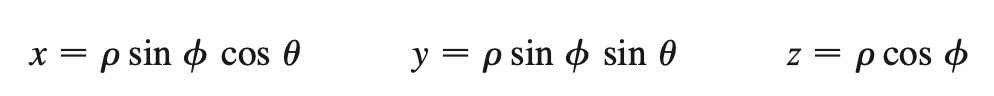
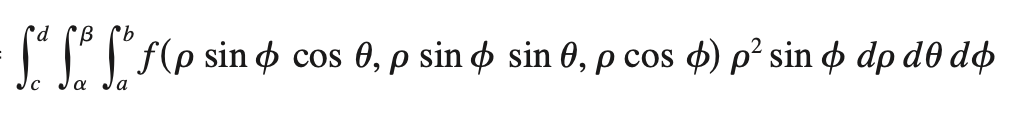
(ρ, θ, Φ)

Jacobian

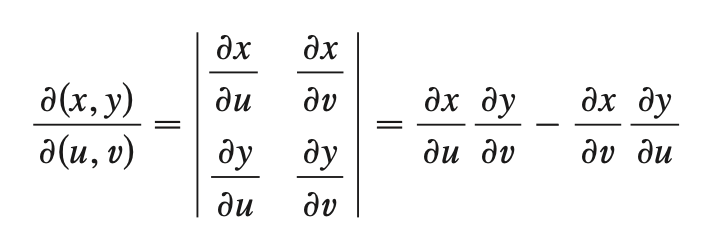
x = g(u, v)

y = h(u, v)

vector fields

assigns each point on the coordinate plane with a vector F(x, y) or F(x, y, z)

conservative vector field

F is conservative if some f exists where:

• F = ∇f

line integral (standard)

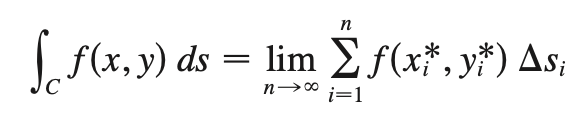
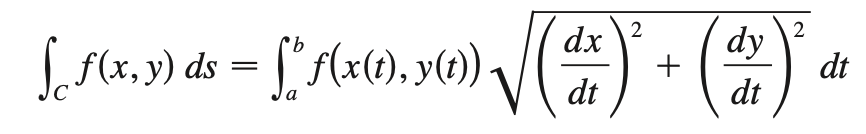
line integral (x’(t))

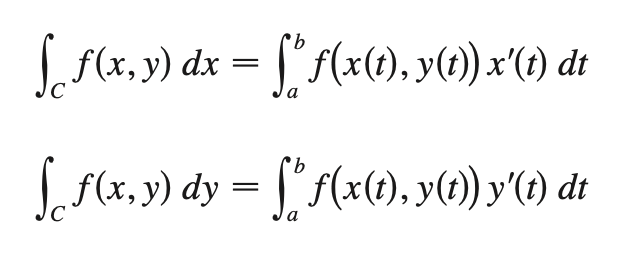
line integral (short form)

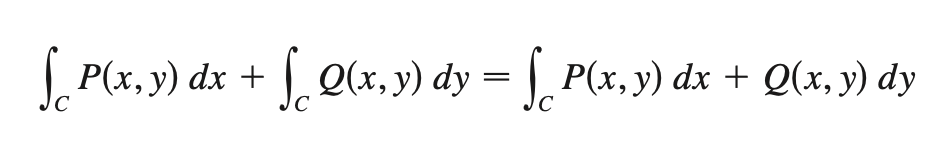
• P integration only considers value change over changes in x

• Q integration only considers value change over changes in y

work done (line integral)

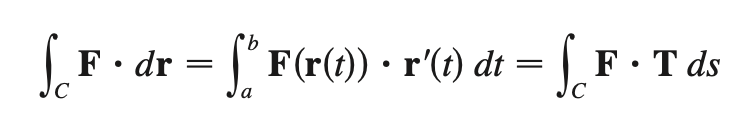
• T = unit tangent on C

Fundamental theorem for line integrals

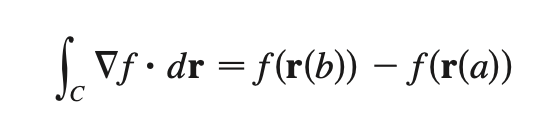
• line integrals of conservative vector fields only require values of f @ C’s endpoints!

test for conservative vector field

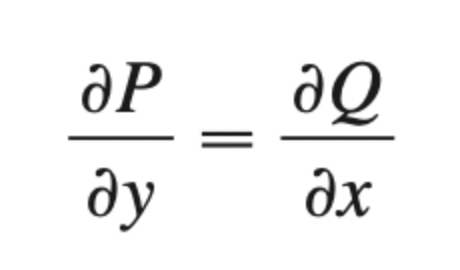
F(x, y) = P(x, y)i + Q(x, y)j

• ONLY true in a simple region

Green’s thm

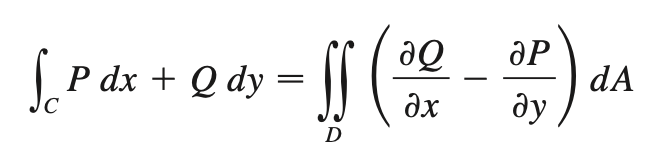
• true if P & Q have continuous partial derivatives on D

Area (region D around closed line integral)

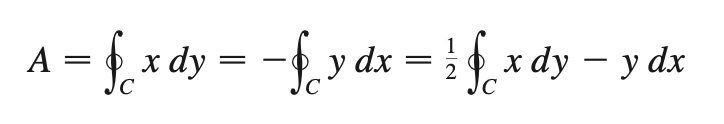
curl

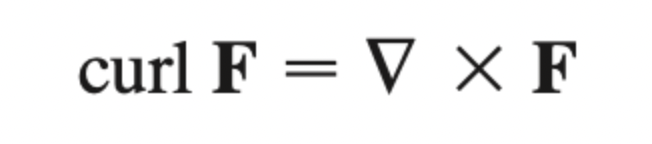
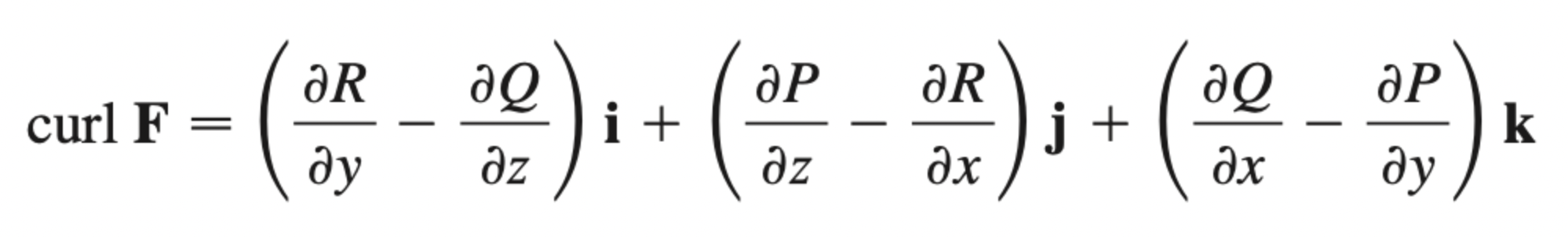
F = Pi + Qj + Rk

• measures rotation in a vector field

curl(∇f)

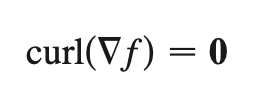
• implies conservative vector fields also have no curl

  • true if second-order partial derivatives are continuous

divergence

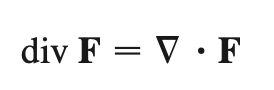
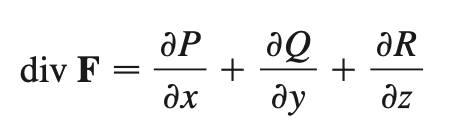
• measures the rate at which vectors move away from a point

div curl

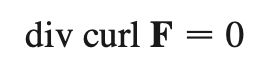
• true if F has continuous second-order partial derivatives

second vector form of green’s thm

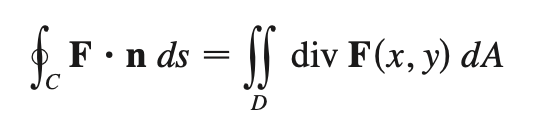
parametric equations of surface S

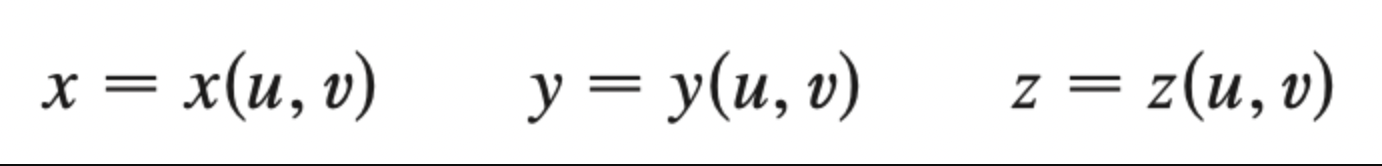
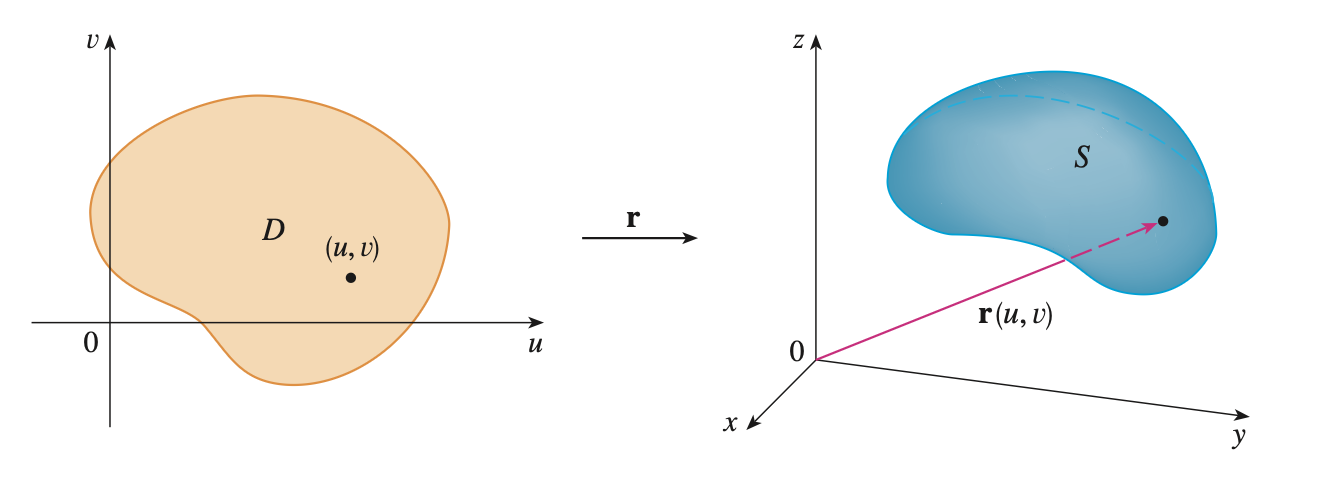
surface of revolution

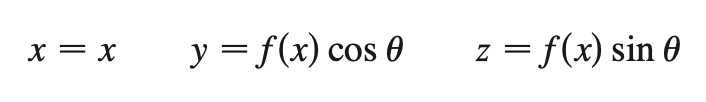
surface area/ surface integral

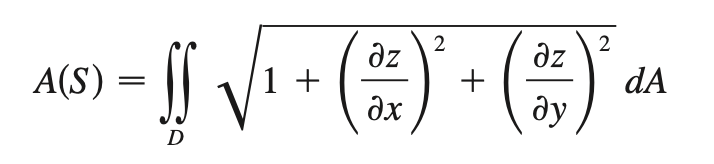
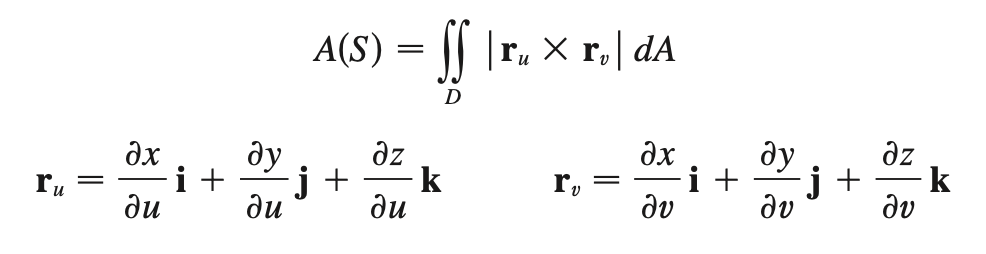
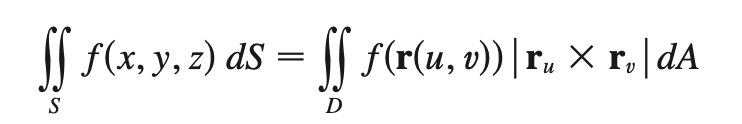
• can be used for COM or moments of inertia

vector surface integrals

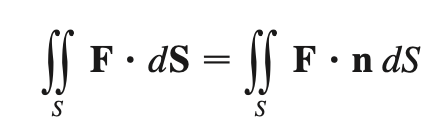
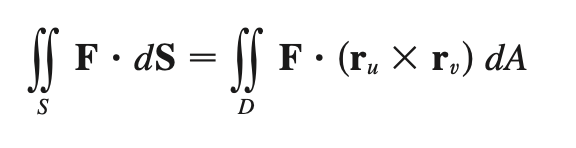
Stokes’ thm

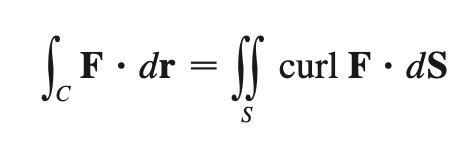
Divergence thm