Two categorical variables

TWO CATEGORICAL VARIABLES

What does the chi-square test of independence/association evaluate? (chisq.test() or associationTest())

It tests whether there is a relationship (association) between two categorical variables.

• H₀: the variables are independent (no association)

  • there is no relationship between the categorical variables

• H₁: the variables are not independent (association exists)

  • there is a relationship between the categorical variables

What is the test statistic for a chi-square test of independence and how are degrees of freedom calculated?

O = observed frequency

E = expected frequency

• Larger X² values correspond to lower probability of H₀ being true

Degrees of freedom: df = (r−1)(c−1)

• r = number of rows, c = number of columns in contingency table

  • the number of levels in both categorical variables

*exact rejection region depends on degrees of freedom

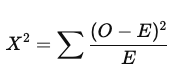
What is Cramer’s V and how is it interpreted? (cramersV())

• Cramer’s V measures the strength of association between two categorical variables

• Values range from 0 (no association) to 1 (perfect association).

Interpretation scale:

• 0–0.15: very weak

• 0.15–0.20: weak

• 0.20–0.25: moderate

• 0.25–0.30: moderately strong

• 0.30–0.35: strong

• 0.35–0.40: very strong

*larger values correspond to a larger deviation from the specified probability distribution under H0

What are the assumptions of the chi-square test of independence?

• Expected frequencies are all at least 5

  • if violated: use Fisher’s exact test (fisher.test())

• Observations are independent

  • if violated: use McNemar’s test (mcnemar.test())