Analytic Geometry, Part 2: Conic Sections (Circle)

When a plane cuts a three-dimensional figure like a cylinder, cone, cube, or the likes, the intersection of the points on the plane and the points on the three-dimensional figure forms a set of points on the plane. This set of points on the plane is called?

Cross Section

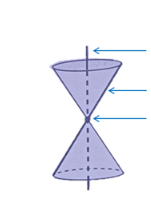
1. Vertical Axis

2. Generator

3. Vertex

Use the plane to cut the two-napped cone in different angles as shown in the next figures. The resulting cross sections are now called?

Conic Sections

They are special curves and are classified into four types, namely circle, parabola, ellipse, and hyperbola.

Conics

When the plane cuts one of the circular cones perpendicular to its vertical axis and parallel to its base, the conic section is a?

Circle

When the cutting plane is parallel to one side of the cone and intersects one of the two cones, the conic section is a?

Parabola

  If the plane cuts the cone in the similar fashion but at a certain angle, then the conic section is an?

Ellipse

Lastly, when the cutting plane intersects the two cones parallel to their vertical axes and perpendicular to their bases, then the conic section is a?

Hyperbola

The equation of the conic section is a second-degree polynomial in two variables; that is?

Ax² + Bxy + Cy² + Dx + Ey + F = 0

It s the set of points on the coordinate plane that satisfies the equation.

Graph or Curve of an Equation

The equation of the circle is a second-degree polynomial in two variables, that is,

Ax²+ Ay² + Dx + Ey + F = 0

It is the center of the circle and the line connecting it to a point on the circle is the radius.

Origin

Standard Forms of the Equation of the Circle:

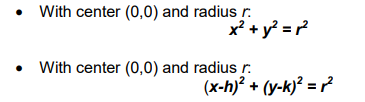
The coefficients of the squared terms are equal and have the same sign

Circle

There is only one squared term

Parabola

The coefficients of the squared terms are not equal but have the same sign

Ellipse

The coefficients of the squared terms have different signs

Hyperbola

A=C

Circle

Either A=0 or C=0

Parabola

AC>0

Ellipse

AC<0

Hyperbola

It is a set of points on the coordinate plane that are of equal distance from a fixed point

Circle

The fixed point of the cirlce is the?

Center

The equal distance of the circle is the?

Radius

The equation of the circle is a second-degree polynomial in two variables, that is:

Ax2 + Ay2 + Dx + Ey + F = 0

This equation is the standard form of the circle whose center is the origin, also referred to as the center-radius form

x2 + y2 = r

This equation is the standard form or the center-radius form of the equation of the circle with a center C(h,k) and radius r.

(x-h)2 + (y-k)2 = r2

It is the set of all points in a plane that are equidistant to a specific point and to a specific line called focus and directrix

Parabola

Vertical Parabola equation:

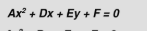
Horizontal Parabola equation:

Standard form of a vertical parabola:

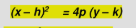
Standard form of horizontal parabola:

The standard equation of a parabola is commonly referred to as the?

Vertex Form

Abscissa

h

Ordinate

k

It is the highest or the lowest point of the parabola, usually denoted as “v”.

Vertex

It is the fixed point of the parabola that is denoted by “f”.

Focus

It is a fixed line that is perpendicular to the axis of symmetry of the parabola and does not intersect to any point in parabola

Directrix

It is a line segment that passes through the focus and parallel to the directrix. Its endpoint and start point lie on the parabola. It also determines the width of the opening of a parabola. Denoted as “4p”.

Latus Rectum

It is the set of all points in a plane whose sum of the distance from two fixed point, foci, are constant

Ellipse

General equation of Ellipse":

Ax² + By² + Cx + Dy + E = 0

Standard equation of Ellipse:

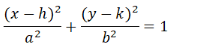
It serves as the reference point for your ellipse

Center

Theye are the points positioned inside the ellipse. It is the one that determines the curvature and shape of the ellipse

Foci

It is the longest line segment that passes through the center. It contains three of the major points in your ellipse, the center and foci. It also determines the axis of the ellipse.

Major Axis

Is it the endpoints of the longest line segment in ellipse or the major axis

Vertex

It is the endpoints of the shortest line segment of an ellipse or the minor axis

Co-vertex

It is the shortest line segment in ellipse that passes through the center and perpendicular to the major axis

Minor Axis

Is unlike to other properties of ellipse, it is not something that can be visually seen. But, it is a property that describes any conic section how it deviates from being a circle. It has a value between 0 and 1

Eccentricity

Is a set of points on the coordinate plan such that the absolute value of the difference of the distances of any point from the two fixed points is constant.

Hyperbola

Equation of the Hyperbola”

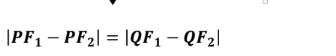
Are the line segments of the hyperbola that contain two points and passes through the foci.

Focal chords or Latera Recta

Are the fixed points in a hyperbola with the distance c which can be contained using c² = a² + b²

Foci

It is the midpoint of the hyperbola F₁F_2, V₁V_2, B₁B₂, and intersection of the asymptote

Center

V₁V₂

Transverse axis

B₁B₂

Conjugate axis

They are thend points of the transverse axis, and the principal axis intersects the hyperbola at these points

Vertices

It is a segment of the principal axis that connects the vertices and has a length of 2a

Transverse axis

Are the endpoints of the conjugate axis with the coordinates of B₁ and B₂

Covertices

It is a segment of the principal axis that connects the covertices and ahs a length of 2b

Conjugate axis

Are the two disconnected curves which extend indefinitely and are asymptotic to the two intersecting lines or the asymptote

Branches

It is the straight line of the curve which the curve approaches indefinitely but never touches

Asymptote