Math 118 Exam 1 Study Guide
0.0(0)
Card Sorting
1/75
Earn XP
Description and Tags
Last updated 12:09 AM on 1/20/23
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No analytics yet
Send a link to your students to track their progress
76 Terms
1
New cards
Area of a circle
A\=πr²
2
New cards
Area of a rectangle
A\=lw
3
New cards
Area of a triangle
A\=1/2bh
4
New cards
Volume of a cylinder
V\=πr²h
5
New cards
Volume of a rectangular solid
V\=lwh
6
New cards
Volume of a triangular prism
V\=(1/2bh)h
7
New cards
Circumference of a circle
C\=2πr
8
New cards
Pythagorean theorem
a^2+b^2\=c^2
9
New cards
Even symmetry: if \_____, then \_____
if (a,b), then (-a, b)
10
New cards
Odd symmetry: If \_____, then \_____
if (a,b), then (-a,-b)
11
New cards
Symmetric about the line y\=x: If \_____, then \_____
If (a,b), then (b,a)
12
New cards
Describe the symmetry between f(x) and the inverse of f(x)
symmetric about the line y\=x
13
New cards
When evaluating a problem and you do not find an answer then it is
undefined
14
New cards
When solving a problem and you do not find an answer then it is
no solution
15
New cards
Is it okay for multiple inputs to give the same output?
yes
16
New cards
Is it okay for one input to give multiple outputs?
no
17
New cards
What are the domain restrictions for a log function?
x \> 0
18
New cards
What is the criteria for functions to be identical/equivalent?
they must have the same domain and ALL the same points
19
New cards
List the asymptotes for y\=2^x
horizontal
20
New cards
List the asymptotes for y\=1/x
horizontal and vertical
21
New cards
List the asymptotes for a log function
vertical
22
New cards
What is a correspondence that *maps* EACH element in x to a UNIQUE element in y?
function
23
New cards
Name the other terms for input (there's 4)
x, domain, independent variable, argument
24
New cards
Name the other terms for output (there's four)
y, range, dependent variable, value
25
New cards
What is evaluating?
finding an output for the given input (at most one answer)
26
New cards
What is solving?
finding all inputs for a given output (infinite answers)
27
New cards
What is finding?
either evaluating, solving, or finding an expression
28
New cards
What is an increasing function?
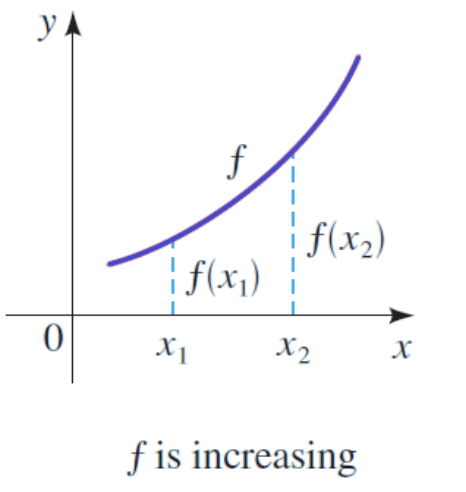
29
New cards
What is a decreasing function?
\
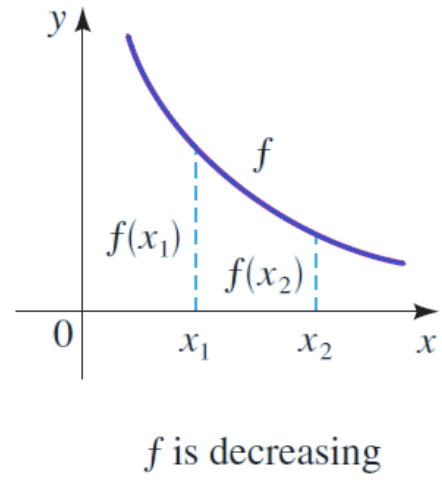
30
New cards
What is a concave up function?
\
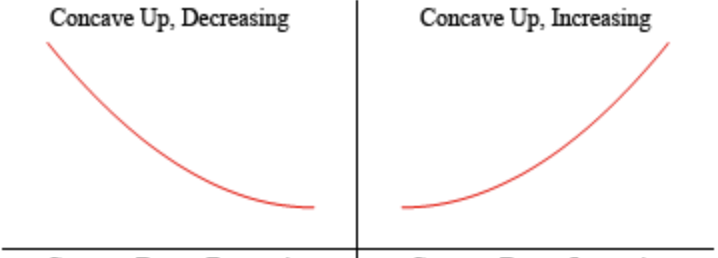
31
New cards
What is a concave down function?
\
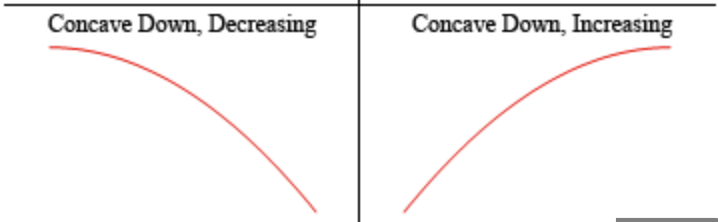
32
New cards
If a function has even symmetry then f(-x) \=
f(x)
33
New cards
If a function has odd symmetry then f(-x) \=
-f(x)
34
New cards
What are three domain restrictions?
can't divide by zero, can't take the square root of a negative number, can't take the log of a negative number or zero
35
New cards
When do you need a sign chart?
if multiple linear factors are in the same even root or the same log
36
New cards
What is an equation for the thing you want to maximize or minimize called?
objective function
37
New cards
If the objective function has more than one input variable, you must find any equations that relate to your input variables. What are these called?
constraint equations
38
New cards
General equation for a vertical shift
f(x) + c
39
New cards
How do you demonstrate a vertical shift on a set of points?
Either add or subtract c from the y-values
40
New cards
General equation for a vertical stretch/compression
cf(x)
41
New cards
When is cf(x) a vertical stretch?
when c is greater than one
42
New cards
When is cf(x) a vertical compression?
when c is greater than zero, but less than one
43
New cards
How do you demonstrate a vertical stretch on a set of points?
multiply y values by c
44
New cards
How do you demonstrate a vertical compression on a set of points?
divide y values by c
45
New cards
General equation for horizontal shift
f(x+c)
46
New cards
How do you demonstrate a horizontal shift on a set of points?
Either add or subtract c from the x-values
47
New cards
If c is positive during a horizontal shift, do you add or subtract c from the x-values?
subtract
48
New cards
If c is negative during a horizontal shift, do you add or subtract c from the x-values?
add
49
New cards
General equation for a horizontal compression/stretch
f(cx)
50
New cards
When is f(cx) a compression?
when c is greater than one
51
New cards
When is f(cx) a stretch?
when c is greater than one but less than zero
52
New cards
How do you demonstrate a horizontal stretch on a set of points?
multiply x-values by the reciprocal of c
53
New cards
How do you demonstrate a horizontal compression on a set of points?
divide x-values by c
54
New cards
What is -f(x)?
vertical flip, reflection about the x-axis
55
New cards
How do the points of a function change when there is a vertical flip/reflection about the x-axis?
x remains unchanged, y switches signs
56
New cards
What is f(-x)?
horizontal flip, reflection about the y-axis
57
New cards
How do the points of a function change when there is horizontal flip/reflection about the y-axis?
x switches signs, y remains unchanged
58
New cards
What must you do if you have a horizontal shift and another horizontal transformation?
factor the argument to see the true shift
59
New cards
Steps for a sequence of transformation
horizontal shift -\> stretches/compressions -\> reflections -\> vertical shifts
60
New cards
When should you plug points into the equation to check you did the transformation correctly?
always
61
New cards
\___________ is the set of numbers in the domain in the domain of a resulting composite function AND the domain of the inner function.
domain of a composite function
62
New cards
In order to ensure a composite function remains a function, you need \_____
domain restrictions
63
New cards
How do you find inverses algebraically?
switch x and y and solve for y
64
New cards
The input of f is the \_____ of f inverse.
output
65
New cards
The input of f inverse is the \_____ of f.
output
66
New cards
If the point (a,b) is on f, then the point \_____ is on f inverse.
(b,a)
67
New cards
Are the domain and range of f and f inverse the same?
no, they switch
68
New cards
f^1(x) is the \_____. (f(x))^1 is the \______.
inverse, reciprocal
69
New cards
What do you do if a function is not one-to-one?
restrict it's domain
70
New cards
Draw y = |x|

71
New cards
Draw y=x^2
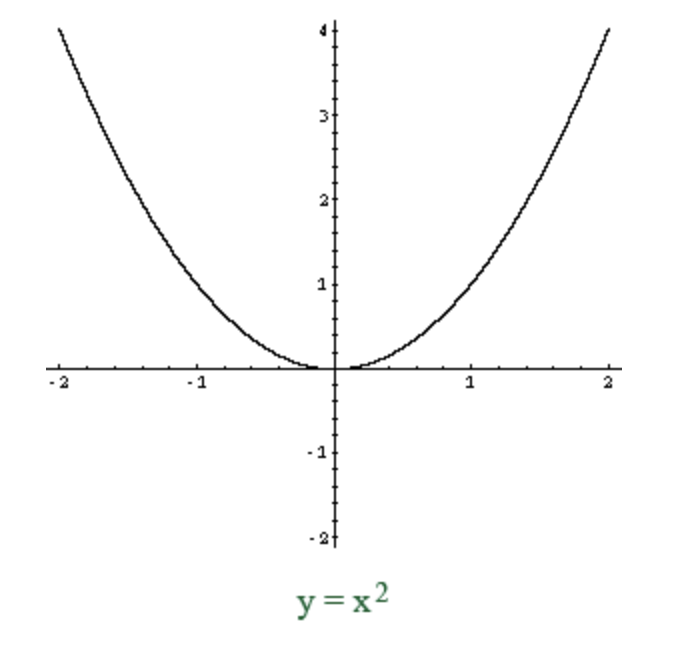
72
New cards
Draw y=x^3
73
New cards
Draw y=√x
74
New cards
Draw y=2^x
75
New cards
Draw y=1/x
76
New cards
Draw y=sin(x)
Explore top notes
Personality 210 Psychology Notes (Part 3) Continuing Traits and Trait Traditions
Updated 1335d ago0.0(0)
Personality 210 Psychology Notes (Part 3) Continuing Traits and Trait Traditions
Updated 1335d ago0.0(0)