ECS 20 Final Review: Chapters 1-8, 10

ECS20 - Prof. Franklin FQ2023

Tree

A connected graph with no cycles.

Tree Fact

If a tree has n vertices, then it has n - 1 edges.

Connected graph

A graph in which there is a path between every pair of vertices.

No-cycle graph

A graph that does not contain any cycles.

Leaf

A vertex of degree 1 in any graph.

1st Theorem of Trees

Every tree with at least two nodes has at least one leaf.

Tree Nodes and Leaves (2nd Theorem)

Every tree with at least two nodes has at least two leaves.

Spanning Tree

A special kind of subgraph made from all vertices of a graph, with no cycles.

Minimum Weight Spanning Tree

A spanning tree with the minimum total weight among all possible spanning trees.

Kruskal's Algorithm

An algorithm for finding the minimum weight spanning tree.

Begin with connected edge-weighted graph.
• Add the lowest-weight edge in graph to solution.
• Consider the remaining edges in increasing order by weight.
• If considered edge doesn’t create cycle, then add it to solution.
• End when # of edges in solution one less than # vertices in graph.

Prim's Algorithm

Another algorithm for finding the minimum weight spanning tree.

Binary Tree

A type of tree with a distinguished vertex called the "root" and at most two edges growing downward from each vertex.

Complete Binary Tree

A binary tree in which every vertex, except for the leaves in the bottom rank, has exactly two edges growing downward.

Binary Search Tree

A binary tree that allows for super-fast search for datum values stored on its vertices.

Matching

A special kind of subgraph made from some of the vertices and edges of a graph, such that every vertex has degree exactly 1.

Perfect Matching

A matching that includes all vertices of the graph.

Perfect Weighted Matching

A perfect matching of an edge-weighted graph that minimizes the sum of weights.

Coin Puzzle

A puzzle involving arranging coins on a grid with certain constraints.

Backtracking Algorithm

An algorithm that builds a solution dynamically by trying different possibilities and backtracking when necessary.

General Backtracking Algorithm

A backtracking algorithm that starts with an empty list and appends possible solution elements, checking for validity and completeness at each step.

Bubble Sort

A sorting algorithm that repeatedly steps through the list, compares adjacent elements, and swaps them if they are in the wrong order.

Spanning Tree Alg: Start Big

Create copy of graph with all vertices, all edges. • systematically remove edges that don’t disconnect anything. • Stop when no edge can be removed without disconnecting something

Spanning Tree Algorithm: Start Small

Create copy of graph with all vertices, no edges. • Systematically add edges that don’t create cycles or more than one tree. • Stop when no edge can be added without creating a cycle.

Binary Search Tree: Magical Search Algorithm

Datum value (value on node)on any vertex ordered after everything below it to left. • Datum value on any vertex ordered before everything below it to right.

If V = root datum value, done. If not

Move to left child if V smaller, right child if V bigger.

Treat new node exactly the same way, and continue recursively.

If any move fails, then report value not found.

(n k) but vertical

n choose k, # of different ways to choose k different items from a pile of n items, where order doesnt matter.

how do you read pascal’s triangle

0th row = first row, first element in row = 0th index

(n k) relation to pascal’s triangle?

n corresponds to the row, and k to element

what is overcounting? how do we use it?

Suppose there are “a” things that have “b” aspects. By product principle, there are a x b variants. But (ab) can be written as c * d, where c represents things and d represents aspects.

Binomial Theorem

(x+y)^n =
summation from k = 0, to n, (n k)x^(n-k)y^k =
(n 0)x^n+ (n 1)x^n-1 y^1 …. etc

How can you calculate (n k)?

n!/k!(n-k)!

(n k) coefficients can be found on:

pascal’s triangle

Pascal’s Identity

( n + 1, k) = (n, k-1) + (n, k)

combinatorial proof (example 1.8m chapter 6 binomials and pascal’s identity)

consider the identity:
the summation from k = 0 , to n, (n, k) (3n, n-k) = (4n, k)
Look at goodnotes for a more visual explanation:
The RHS: Can be thought of as picking any candy from the bag while..

LHS: can be seen as picking candy as either lemon or strawberry, subsets of a bag. The number of ways to do this depends on k, which is why we need to add up the possibilities.

The Sum Principle

# of elements in a finite number of disjoint finite sets, a…b…n is the sum of their sizes. |A| + |B| +…..+|N|

The Product Principle

|A| x |B| x ……. x |N|

Defintion

precise statement of meaning of term

conjecture

proposed statement with supporting evidence

theorem

statement with a proof

lemma

small statement used to prove some bigger statement

corollary

something that follows directly from related theorem

proof

argument so convinving it compels consent

direct proof

simple proof “template”

N is even if..

2 is a divisor or n = 2k for some k

N is odd if

2 is not a divisor or n = 2k + 1 for some K

N is prime if

positive divisors are 1 and itself.

N is binary if

consists of 1’s and 0’s

Goldbah’s Conjecture

every even number can be written as the sum of two primes.

When counting total subsets, a set has…

2^n subsets

First Proof Of Counting Subsets

Proof by Product Principle: Every subset of S corresponds to a choice about whether to include its 1st element, whether to include its 2nd element, and so forth, ending with a choice about whether to include its nth element.
number of ways of these choices is size ofCartesian product {1 st element yes, 1st element no> x {2nd element
yes, 2nd element no}. By product Principle it’s 2^n

2nd Proof of Counting Subsets

Every subset of a set of n elements corresponds to a binary string of n 0’s and 1’s, where 0 means don’t include that element and 1 means
do include that element…counts the number of binary strings of length n by considering the integer values of these binary strings.

Piegeonhole Principle

If you have more than k times as many pigeons as pigeonholes, then
some pigeonhole must have more than k pigeons in it.

What is a direct proof?

”if p then q” or ”p implies q” which we can write as p ⇒ q. assume original statement p to be true, and use it to show directly that another statement q is true.

Example of direct proof:

Proving that if you add two even numbers, you’ll get an even number.

• Assume a=2k for some integer k.

• Assume b=2m for some integer m.

• Consider a+b=2k+2m.

• Factor out the common factor of 2: a+b=2(k+m).

• Since k+m is an integer, a+b is even.

What is proof by contradiction?

begin by assuming P is false and show that this
leads to a contradiction; something that always false.
P ⇒ ∼Q. (negation of Q)

Example of proof by contradiction:

Proof by Contrapositive:

proving something by flipping it around and negating both parts. If the flipped-around statement is true, then the original statement is also true. It's like saying, "If it's not the case that 'B' happened, then it's not the case that 'A' happened either."

Simple Example:

Statement: If it's raining, then the ground is wet.

Contrapositive Statement: If the ground is not wet, then it's not raining.

Explanation: To prove the original statement by contrapositive, we show that if the ground is not wet (contrapositive), then it's not raining. If we observe a dry ground, it means it's not raining, supporting the original statement.

what is a set

collection of distinct elements called members

cardinality | |

number of distinct elements in a finite set A

0 with slash set

empty set

What sets are Z, N and Z_2

set of itegeres, positive integers (natural numbers), binary digits

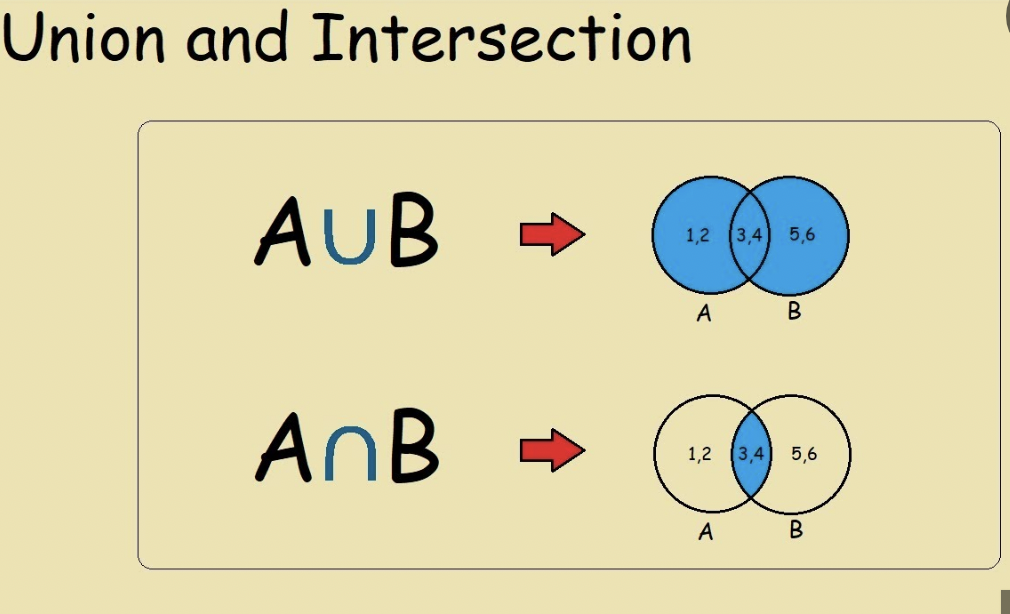
A U B

union of sets A and B, set of all elements in either A or B

A ⋂ 𝐵

intersection of sets A and B; set of all elements in both A or B

A\B

difference of sets A and B ( A - B); set of all elements in A but not in B

A with Line on Top

Complement of set A; set of all elements not in A, but in some implied universe U

Example of A ⋃ 𝐵

If A = {1, 2, 3} and B = {2, 3, 5, 8}, A ⋃ 𝐵 = {1, 2, 3, 5, 8}

Example of A ⋂ 𝐵

If A = {1, 2, 3} and B = {2, 3, 5, 8}, A ⋂ 𝐵 = {2, 3}.

Example of A\B or A-B

f A = {1, 2, 3} and B = {2, 3, 5, 8} then A – B = {1} and B – A = {5, 8}.

A C B (line under C)

Set A is a subset of Set B; elements of A are drawn from set B, possibly missing some elements of B.

A C B (line and / under C)

The elements of A are drawn from set B, missing at least one element

a E A

a is a member of set A

{x in A | P(x)}

he set of elements of set A with property P.

example: { x in integers Z | x prime and x < 15 }

Double Inclusion:

If A is a subset of B and B is a subset of A, this implies that A=B.
If A is contained within B and B is also contained within A, then both must be equal.

What is a proposition?

Statement that can etiher be true or false, variables are p q r

Truth tables: AND

borh p and q need to be true P ^ Q

Truth tables: OR P V Q

either p or q can be true for p v q to be true

what is the logical operator for negation?

gun pointing to the left

Review Notes for Exclusice-or, Biconditonal or Implies

Biconditional P←→Q p implies q and q implies p

true when p and q both true or both false.

DeMorgan’s Law

¬ ( p ⋀ q ) logically equivalent to ( ¬ p ) ⋁( ¬ q )

¬( p ⋁ q ) logically equivalent to ( ¬ p ) ⋀ (¬ 𝑞 )

Proof by Contradiction Template:

Restate theorem as If ( conditions ) true, then ( conclusion ) true.
• Write out (conditions) and negation of (conclusion) on scratch paper.
• Try to derive any contradiction, any contradiction means you’ve proven it.

Proof by Contrapositive Template:

you flip and negate both

Restate the theorem as If ( conditions ) are true, then ( conclusion ) are true.
• Write the negation of (conclusion) on scratch paper.
• Try to simplify the negation of (conclusion) to understand it better.
• Try to derive the negation of (conditions).
• If you do derive the negation of (conditions), you have proven the
theorem.

Function: A → B is a function from set A (“domain”) to set B (“Target”) if….

every element a in A is mapped to unique element f(a) in B.

(f(a) called image of function at a, set of all images called range)

GIPO

May have elements of A not mapped, or mapped to more than one thing

One-to-One or Injective:

At most one arrow ending at each element of B

Onto, or surjective:

At LEAST one arrow ending at each element of B

Bijection

Exactly one arrow ending at each element of B
|A| = |B|

If one-to-one, |A| ? |B…
injective, surjective, bijective>

|A| > |B|, injective

Forest

graph with no cycles, disconnected

Tree

Connected graph with no cycles

C_n

graph with n vertices with one big cycle

P_n

graph with n vertices and one big path

k_n

graph with n vertices and all possible edges, but no self edges

Graph isomorphism Def. informal

Two graphs are isomorphic if there is a way to relabel the vertices of one so that the edge sets of both are identical.

Graph Isomorphic, Formal Def.

Two graphs G and H “isomorphic” if there exists a bijection f
from vertices of G to vertices of H, such that v --- w is an edge of G ←→ f (v ) --- f ( w ) is an edge of H

Induction Template

Base case: Check to make sure that whatever you want to prove holds for small natural
numbers, like 1, 2, or 3.

Inductive hypothesis: Assume that whatever you want to prove is true, as long as the
variable in the statement is smaller than or equal to k; here, k is a specific (but unknown)
value.
Inductive step: Consider the statement with k +1 as the variable. Use your knowledge that
the statement is true when the variable is less than or equal to k in order to show that it’s still true
for k +1. (That is, use the base case(s) and inductive hypothesis.)

64 ≡ 29 (mod 7)

64/7 = 9 × 7 + 1
29/7 = 4 X 7 + 1

the remainder is the same for both, which is one, so is true.

What is the 3n + 1 Algorithm?

input is some positive intger n
if n = 1; stop
if n is odd; n = 3n + 1
else if n is even; n/2

What are the properties of an equivalence relation?

This is an equivalence relation:
• Symmetric: If x same sign as y, then y same sign as x.
• Transitive: If x same sign as y, and y same sign as z, then x same sign as z
• Reflexive: x has same sign as x.

Give an example of an equivalence relation, if integers x and y are congruent modulo 4

Equiv class [ 0 ] = { integers a | a mod 4 = 0 } = { ..., - 4 , 0 , 4 , ...}
• Equiv class [ 1 ] = { integers a | a mod 4 = 1 } = { ..., -3 , 1 , 5 , ...}