LOgic Fianl study guide! So you won't fail

this is deductive logic in a pack!

formal logic

A system of reasoning based on strict principles and rules, used to validate arguments and deduce conclusions logically. It often involves symbolic language and structured forms of reasoning.

informal logic

A type of reasoning that focuses on argumentation, evaluation of everyday language, and the various ways in which arguments may be constructed or deconstructed, often lacking formal structures.

dialectical logic

A form of reasoning that emphasizes the development of ideas through dialogue and contradiction, focusing on the resolution of differences and the synthesis of opposing views.

axiom

a statement that is either true or false

term

A word or phrase that represents a class or related things

deductive logic

A type of reasoning that starts with general principles or premises to reach specific conclusions. It is often characterized by wither being with valid or invalid

Inductive Logic

A form of reasoning that draws general conclusions from specific observations or instances, often involving probability rather than certainty. Evaluated as either being string or weak.

Evidence

Any information or data used to support a conclusion or argument. that can be classified as being valid or invalid

*A priori *Truths

Statements known to be self-evident, self-proving, and independent of specific evidence or experience.

Categoril Logic

A branch of logic dealing with syllogisms and the relationships between categories, their basic building blocks are called a term, and its building blocks are connected by a “being verb” or copula.

Propositional Logic:

Propositional logic’s basic building block is a statement, called a proposition, and its building blocks are connected by logical operators.

Stoics:

The Stoics loved to study complex arguments, propositions, and paradoxes that did not fit in in the Aristotelian system of logic.

Thomas Aquinas:

Thomas Aquinas used Aristotelian logic to develop arguments for the existence of God. 

William of Okham:

William of Okham told us that “Logic is the most useful tool of all the arts.”

George Boole:

He developed a system of symbolic logic known as Boolean logic. This system provided a logical framework for dealing with arguments or propositions about categories of things that didn't actually exist or that were hypothetical possibilities. Boole also developed a logical system that applied to math, which became known as Boolean algebra. 

John Stuart Mill:

He explored rules that could help scientists determine cause-and-effect relationships. His methods were and still are applied in many scientific, medical, social, and psychological sciences.

Syllogisms:

They are a special kind of three-statement argument; they include two premises and a conclusion. 

Inductive Inference:

Inductive inference is when we take propositions we gather from our observations of the world around us and use them to make educated guesses about things we haven't seen yet. 

Simple Apprehension:

Occurs when we put things into groups, classes, or categories in our minds. 

Judgment:

A thinking process that occurs when a person expresses a relationship between two terms; a mental process by which we recognize and name an object. 

Inference:

A reasoning process through which a person arrives at new information through the implications of other axioms, postulates, or observed examples. 

Propositions:

A single declaration or report of facts or opinions. 

Truth-Value:

The truth or falsity of a proposition or statement. 

True:

Has the right understanding of reality.

False:

Has the wrong understanding of reality. 

Questions:

Sentences that ask about issues or ideas to get someone else's view.

Commands:

Verbal statements that instruct someone to perform an action. 

Greetings:

Verbal expressions that communicate welcome or hospitality to a person or a group of people. 

Exclamations:

Verbal expressions which are indications of strong emotion, such as surprise, anger or happiness. 

Nonsense Sentences

Sentences that don't make sense or don't match what's real.

Self-Reports:

Expressions of feeling or belief.

Premise Indicator:

Words or phrases that indicate that the premises are about to follow.

Conclusion Indicator:

Words or phrases that indicate that the conclusion is about to follow. 

Premise:

A reason given that leads to the arguer’s conclusion. 

Conclusion:

What a person believes based on evidence; the point of persuasion in a syllogism; that which the speaker is hoping his audience will be persuaded to do or believe; the last statement in an argument. 

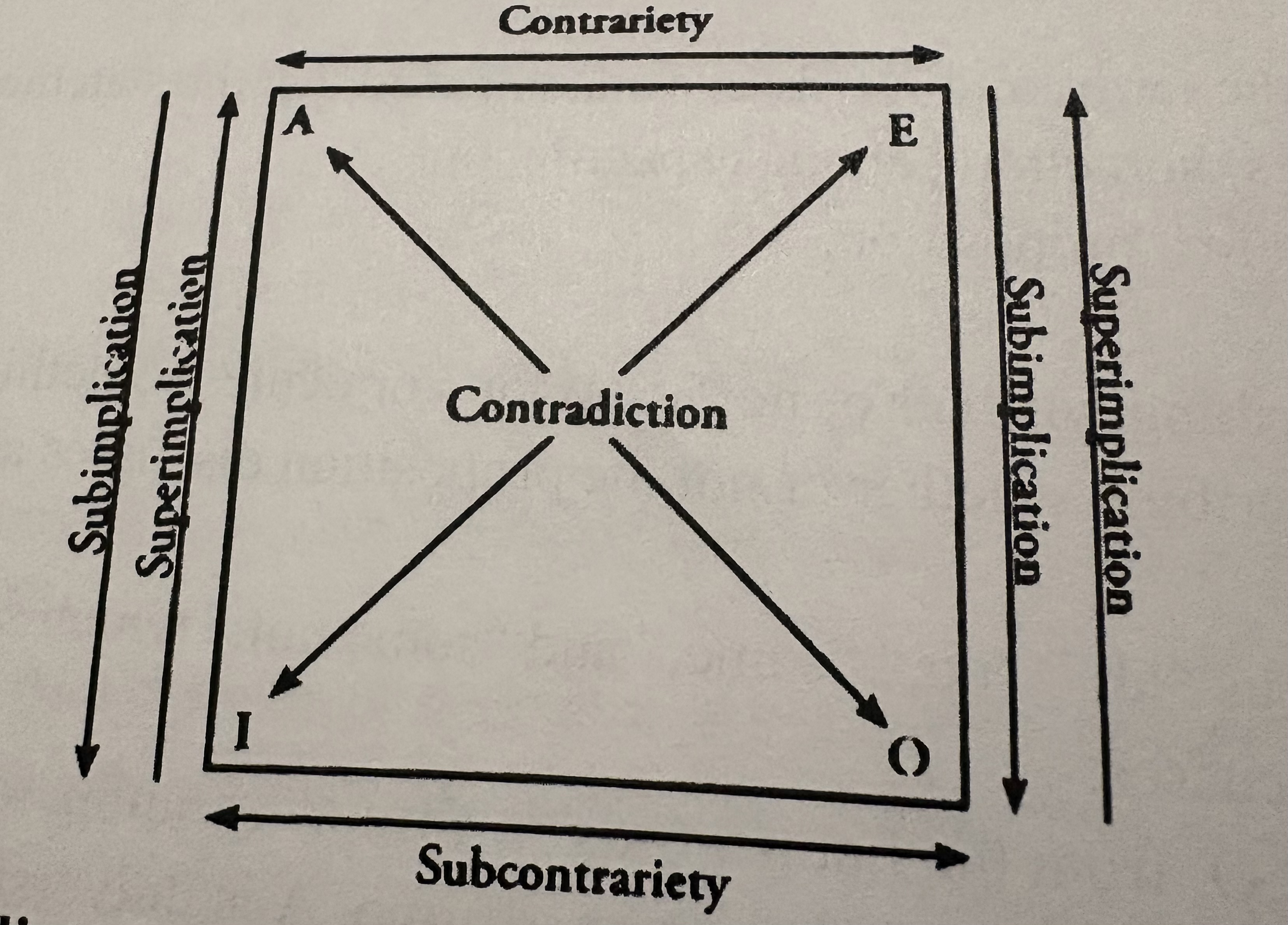
Square of opposition

A diagram that illustrates the relationships of opposition

Subject Term:

The term in a proposition about which the proposition is written. It is the first noun term in the proposition. 

Predicate Term:

The term in a proposition that follows the verb and renames or describes the subject. 

Categorical Form:

The arrangement of the terms and words in a statement so that the statement either affirms (supports) or negates (denies) something about a specific topic.

Subject Term:

The term in a proposition about which the proposition is written. It is the first noun term in a proposition. 

Predicate Term:

The term in a proposition that follows the verb and renames or describes the subject. 

Verb of Being:

Also known as “being verb.” Am, is, are, was, were, be, being, been, have, has, had, do, does, did,.....

Copula:

The logic name of the being verb in a proposition.

Quality:

The aspect of a proposition describing whether or not it supports or denies something.

Quantity:

The aspect of a proposition describing whether or not the proposition discusses all or some things.

Quantifier:

A word in a proposition, such as “all,”(A) “no,”(E) “some,”(I) and “some not,”(O) which signals the amount of a class that a proposition discusses. 

Categorical Propositions:

A proposition that either confirms or denies something about a class of things.

Quality of a Proposition:

The aspect of a proposition describing whether or not it supports or denies something. 

Quantity of a Proposition:

A word in a proposition, such as “all,” “no,” “some,” and “some not,” which signals the amount of a class that a proposition discusses.

Universal Propositions:

A statement that affirms or denies something about all of a category represented by a term. 

Particular Propositions:

A proposition that affirms or denies something about some of the members of a category represented by a term. 

Universal Affirmative Propositions:

A proposition that affirms something about all of a category. 

Universal Negative Propositions:

A proposition that denies something about all of a category. 

Particular Affirmative Propositions:

A proposition that affirms something about some of the members of a category represented by a term. 

Particular Negative Propositions:

A proposition that denies something about some of the members of a category represented by a term.

Contradiction:

The relationship of opposition that exists between A and O  propositions and E and I propositions. Contradictory statements cannot both be true or both be false at the same time. 

Rules for Contradiction

• Contradictory propositions cannot both be true at the same time.

• Contradictory propositions cannot both be false at the same time.

• If one contradictory proposition is true, the other is false.

• If one contradictory proposition is false, the other is true. 

Contrariety: 

The relationship of opposition that exists between A and E propositions. A and E propositions cannot both be true at the same time, but they can be false at the same time.

Rules for contrarity

• Contrariety is the relationship between A and E propositions.

• Propositions of contrariety cannot both be true at the same time. 

• Propositions of contrariety can both be false at the same time. 

• If one contrary proposition is true, the other is false. 

• If one contrary proposition is false, it does not necessitate that the other is true.

Subcontrariety:

A relationship of opposition that exists between I and O propositions. Subcontrary statements cannot both be false, but they can both be true.

rules for subcontrarity

• Subcontrariety is the relationship between I and O propositions.

• Propositions of subcontrariety can both be true at the same time. 

• Propositions of subcontrariety cannot both be false at the same time. 

• If one subcontrary proposition is true, it does not necessitate the falsity of the other.

• If one subcontrary proposition is false, then the other is true. 

Subimplication (subalternation)

: A relationship that exists between A and I propositions and E and I  propositions. The truth of the universal implies the truth of the particular. 

rules for subimplication

• Subimplication is the relationship that exists between universal and particular propositions. A relates to I; E relates to O. 

• The truth of the universal implies the truth  of the particular. 

• The falsity of the universal does not imply the truth or falsity of the particular.

Superimplication (superalternation):

The relationship of opposition that exists between I and A propositions and O and E propositions. The falsity of the particular implies the falsity of the universal.

rules for superimlication

• Superimplication is the relationship between particular and universal propositions. I relates to A; O  relates to E. 

• The truth of the particular proposition does not necessitate the falsity of the universal. 

• The falsity of the particular proposition implies the falsity of the universal.

• The relationships on the square of opposition are considered relationships of opposition because they demonstrate how the truth-values of propositions are related to one another.

• The purpose of the square of opposition is to determine how propositions are in opposition to each other or what they imply about each other. 

Infer

Infer means to derive an idea from what we already know, while to imply means to express or state something indirectly because what was said involves another truth as a necessary or logical consequence.

Immediate Inferences:

Another name for the relationships of equivalence, which tell us what equivalent statement a proposition immediately implies or to which it is identical. 

Obversion:

A relationship of equivalence that occurs when the quality of the subject of a proposition is changed and then the predicate is negated. It can be performed on all propositions.

All S is P → No S is non-P.

Conversion:

The relationship of equivalence that occurs when you switch the subject and the predicate of a proposition. It only works on I and E propositions.

No S is P→ No P is S. 

Contraposition:

The relationship of equivalence that occurs when you obvert a statement, then convert it, and then obvert it again. It exists only for A and O propositions.

All S is P→No S is non-P→No non-P is S→All non-P is non-S. 

Clarification for relationships of equivalence

The relationships of equivalence clarify confusing propositions and examine a proposition from different angles.

Argument:

A statement of rational reasons for or against an idea or action with the intent to persuade. 

Syllogism:

A formally arranged argument containing two premises (major and minor), a conclusion, and three terms. Further, the syllogism is arranged in the following order: major premise, minor premise, conclusion. 

Categorical syllogism:

Conclusion:

What a person believes based on evidence; the point of persuasion in a syllogism; that which the speaker is hoping his audience will be persuaded to do or believe; the last statement in an argument.

Enthymeme:

An(stupid) abbreviated form of a syllogism in which one of the premises is missing. 

First-Order Enthymeme:

A syllogism that omits the major premise.

Second-Order Enthymeme:

A syllogism that omits the minor premise. 

Third-Order Enthymeme:

A syllogism that omits the conclusion. 

Implied Premise:

A premise that is not directly stated but that can be inferred from the other premise and the conclusion of a syllogism. 

Implied Conclusion:

A conclusion that is not directly stated but can be inferred from the premises of a syllogism.

Mood:

The manner in which a syllogism’s propositions are arranged according to quality. 

Figure:

The way in which the middle term is arranged in a syllogism. 

Schema:

The pattern of organization identified by its mood and figure in a syllogism. 

Major term:

The predicate of the conclusion, and the term that appears in the major premise. 

Minor term:

The subject of the conclusion of a syllogism. It appears in the minor premise. 

Middle term:

The term that appears twice in the premise in the premises of a syllogism but not in the conclusion. It links the major and minor terms. 

Major premise:

The first premise in a properly structured syllogism; contains the major term.

Minor premise:

The second premise in a properly structured syllogism; contains the minor term. 

Valid:

An adjective describing a deductive argument that is structured properly, or uses right reasoning form. Inductive arguments are considered “strong” or “weak,” whereas deductive arguments are considered valid or invalid. 

Invalid:

Refers to an argument that has a conclusion that is not supported by its premises. It describes a deductive argument that is structured incorrectly. 

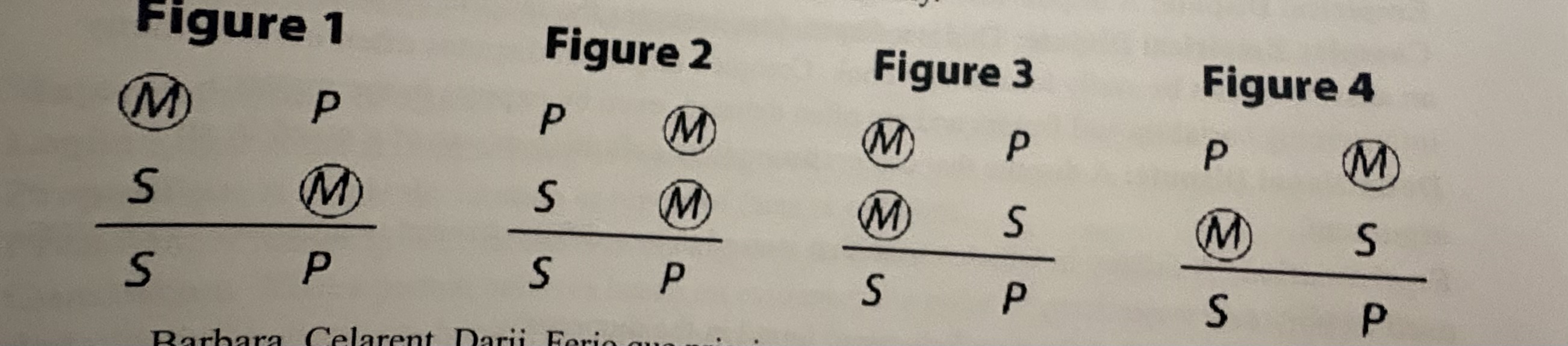
Valid syllogism:

A syllogism that is structured correctly. 

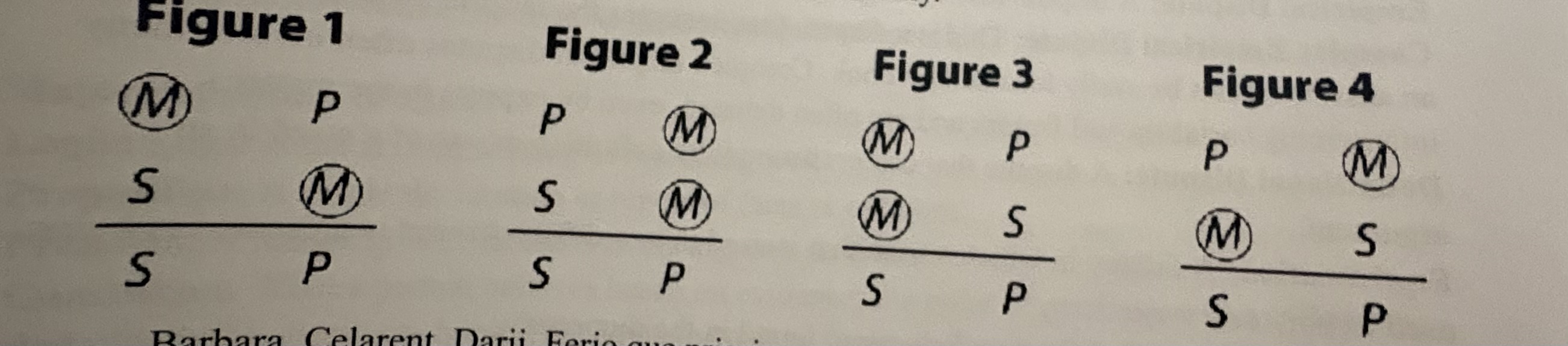
True syllogism:

A syllogism that is factually accurate and correct.  

Sound syllogism:

A syllogism that is both true and valid. 

Counterexample Method: A method for determining the validity of syllogisms in which a person attempts to find a syllogism in the same schema that has true premises leading to a false conclusion. If a syllogism like this is found, it proves that the syllogism schema is invalid.

Fallacy of Four Terms:

A formal fallacy that occurs when a syllogism contains four terms, or when a syllogism uses three terms, one of which is used in two different ways. 

Equivocation:

A fallacy in which a term is used in two different ways is presented as being used in only one way.

Validity:

An adjective describing a deductive argument that is structured properly, or uses right reasoning form. Inductive arguments are considered “strong” or “weak,” whereas deductive arguments are considered “valid” or “invalid.” 

Distributed Terms:

A quality that describes a term that is talking about all of the members represented by that class. 

Undistributed Terms:

A term is undistributed when only some of a class is referenced in a proposition.