Math 2 - Practice Problems 3.1 - 3.2 Review

Flashcards to review key concepts and properties of parabolas and quadratic functions based on practice problems 3.1-3.2.

The __ of a parabola is its turning point.

vertex

The x-intercepts are the points where the parabola crosses the __-axis.

x

The y-intercept is the point where the parabola crosses the __-axis.

y

The __ of a parabola represents all possible x-values.

domain

The __ of a parabola represents all possible y-values.

range

The interval of __ is where the y-values of a parabola are getting larger.

increase

The interval of __ is where the y-values of a parabola are getting smaller.

decrease

The __ of symmetry is a vertical line that divides the parabola into two identical halves.

axis

The vertex of a parabola indicates either a maximum or a __ value.

minimum

The general form of a quadratic function 𝑓(𝑥) = 𝑎(𝑥 − ℎ)2 + 𝑘 is known as the __ form.

vertex

For the function 𝑓(𝑥) = − 3(𝑥 − 2)2 + 7, the value of 'a' is __.

-3

For the function 𝑓(𝑥) = − 3(𝑥 − 2)2 + 7, the value of 'h' is __.

2

For the function 𝑓(𝑥) = − 3(𝑥 − 2)2 + 7, the value of 'k' is __.

7

The vertex for the function 𝑓(𝑥) = − 3(𝑥 − 2)2 + 7 is __.

(2, 7)

Since the 'a' value in 𝑓(𝑥) = − 3(𝑥 − 2)2 + 7 is negative, the graph will open __.

down

The equation of the axis of symmetry for 𝑓(𝑥) = − 3(𝑥 − 2)2 + 7 is x = __.

2

If a parabola opens down, its vertex represents a __ value.

maximum

The domain for any standard parabola is always all real numbers or _________.

(-∞, ∞)

If a parabola has a vertex of (10, 18) and opens down, its range is (-∞, __].

18

In the toy rocket application, the number of seconds the rocket is in flight relates to the __ of its parabolic path.

domain

The general form of a quadratic function f(x) = a(x - h)^2 + k is known as the______ form

vertex

To locate the x-intercept(s) in a table of quadratic values, look for rows where the ___-value is 0.

y

The y-intercept from a table of quadratic values is found by identifying the point where the ___-value is 0.

x

Vertex __________

(2,-4)

y - intercept __________

(0,8)

Will the graph open up or down ________

up

what is the a - value ________

3

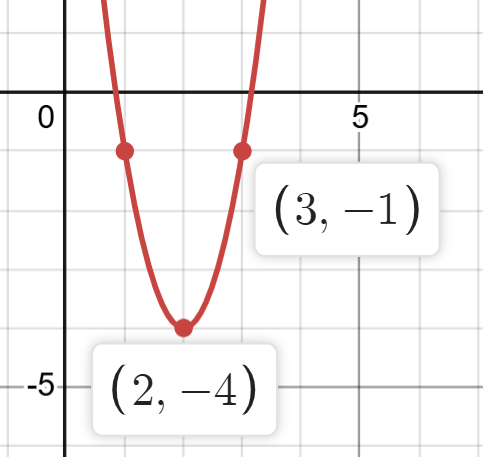
What is the a - value _________

3

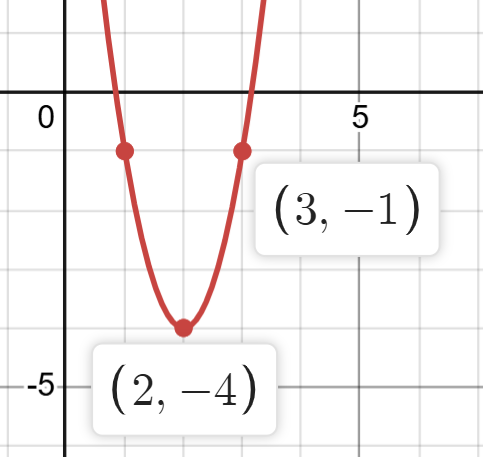
Write the equation ______________

y=3(x - 2)² - 4

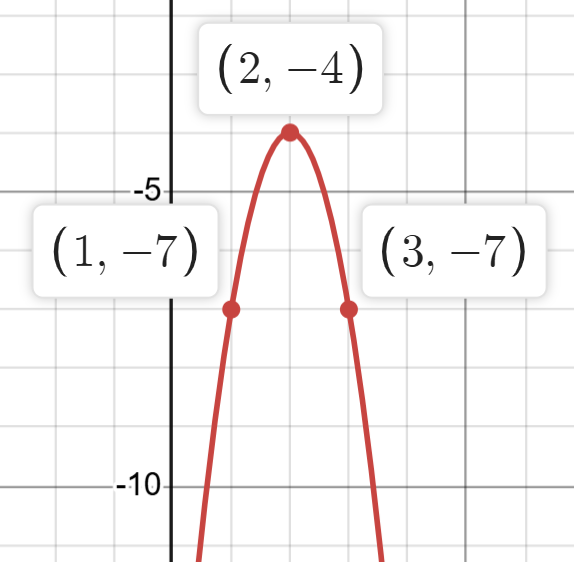
Write the equation 

y = - 3(x - 2)² - 4