Truth Tables and Gates, proof of implies

And

Rewrite: min(p, q)

Algebraic: p · q

Or

Rewrite: max(p, q)

Algebraic: p + q - (p · q)

Negation

Algebraic: 1 - p

Implies

Rewrite: not p or q

Algebraic: 1 - p + p·q

If and only if (iff)

Rewrite: (p implies q) and (q implies p)

Algebraic: p · q + (1 - p)(1 - q)

Questions for all of them

And: are they both 1?
Or: is there a one?

Implies: you know this

Iff: are they the same:

XOR: are they different?

Contrapositivity Theorem

For p, q propositions:

p implies q equiv to:

neg q implies neg p

Can prove by truth table

Identity Law 1

p and 1 ≡ p

Identity Law 2

p or 0 ≡ p

Domination Law 1

p or 1 ≡ 1

Domination Law 2

p and 0 ≡ 0

Negation Law 1

not (not p) ≡ p

Negation Law 2

p or (not p) ≡ 1

Negation Law 3

p and (not p) ≡ 0

Idempotent Law 1

p and p ≡ p

Idempotent Law 2

p or p ≡ p

Commutativity Law 1

p and q ≡ q and p

Commutativity Law 2

p or q ≡ q or p &

Identity Laws

p and 1 ≡ p, p or 0 ≡ p

Domination Laws

p or 1 ≡ 1, p and 0 ≡ 0

Negation Laws

not (not p) ≡ p, p or (not p) ≡ 1, p and (not p) ≡ 0

Idempotent Laws

p and p ≡ p, p or p ≡ p

Commutativity Laws

p and q ≡ q and p, p or q ≡ q or p &

De Morgan's Law 1

¬(p ∧ q) ≡ ¬p ∨ ¬q

De Morgan's Law 2

¬(p ∨ q) ≡ ¬p ∧ ¬q

Absorption Law 1

p ∧ (p ∨ q) ≡ p

Absorption Law 2

p ∨ (p ∧ q) ≡ p

Distributive Law 1

p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)

Distributive Law 2

p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)

Associative Law 1

(p ∨ q) ∨ r ≡ p ∨ (q ∨ r)

Associative Law 2

(p ∧ q) ∧ r ≡ p ∧ (q ∧ r)

De Morgan's Laws

¬(p ∧ q) ≡ ¬p ∨ ¬q

¬(p ∨ q) ≡ ¬p ∧ ¬q

Absorption Laws

p ∧ (p ∨ q) ≡ p

p ∨ (p ∧ q) ≡ p

Distributive Laws

p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)

p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)

Associative Laws

(p ∨ q) ∨ r ≡ p ∨ (q ∨ r)

(p ∧ q) ∧ r ≡ p ∧ (q ∧ r)

(p =⇒ q) ≡

(¬q) =⇒ (¬p)

Theorem 3. 1.2.2 (p =⇒ q) ≡ (¬q) =⇒ (¬p) step 1

Theorem 3. 1.2.2 (p =⇒ q) ≡ (¬q) =⇒ (¬p) step 2

Theorem 3. 1.2.2 (p =⇒ q) ≡ (¬q) =⇒ (¬p) step 3

Theorem 3. 1.2.2 (p =⇒ q) ≡ (¬q) =⇒ (¬p)

Theorem 4. 1.2.3 Proving DeMorgan’s Law

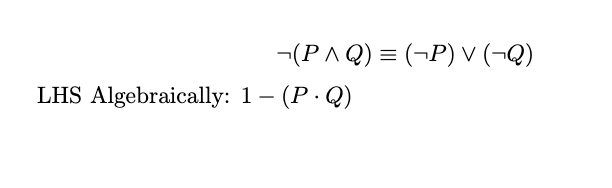
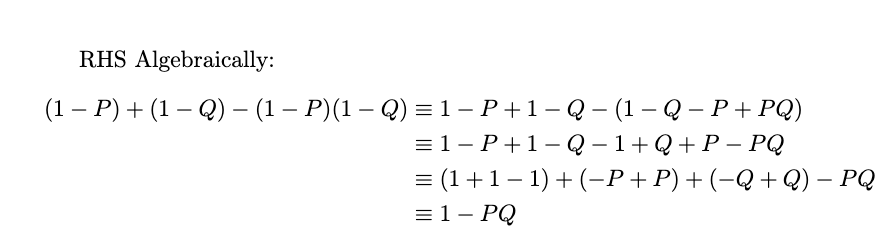
1.2.4 Gates Fan-in and fan-out, and gate

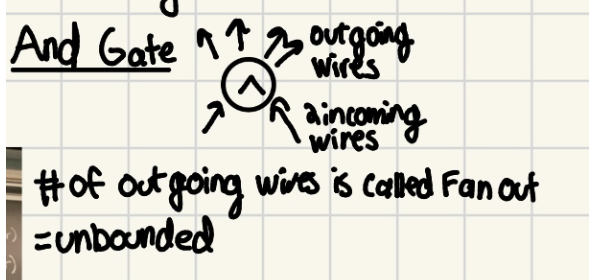
Fan-in: 2

Fan-out: unbounded

1.2.4 Gates Fan-in and fan-out, or gate

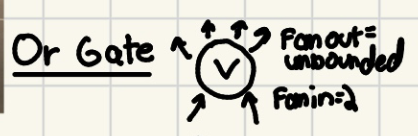
Fan-in: 2

Fan-out: unbounded

1.2.4 Gates Fan-in and fan-out, not gate

Fan-in: 1

Fan-out: unbounded

1.2.4 Gates Fan-in and fan-out, input gate

Fan-out: 1

Fan-in: 0

The final output gate is either

1.2.5 Formulas

special circuits where every gate has fan out ≤ 1

1.2.6 Satisfiable and not satisfiable equations

What it sounds like, some expressions will never evaluate to True

1.3.1 Prefix string encoding:

Start at top, then go left to right.

1.3.2 Quantifiers

Where x is unknown, the expression x² + 8 = 17 is not a valid proposition, but

it can be made into one by using a quantifier.

Existential Quantifier ∃

(∃x P (x))

There exists an x such that P (x) is true.

Common number sets:

• Complex numbers: C

• Real numbers: R

• Real numbers: ∀

1.3.3 Transformation Rule (Quantifiers)

¬(∀x P (x)) ≡ ∃x ¬P (x)

¬(∃x P (x)) ≡ ∀x ¬P (x)

1.3.4 One Bit Addition