AP Biology - Elements of Experimental Design & The Laboratory Experience

Complete review of experimental design and lab skills for AP Biology, covering all required CED concepts. Includes variables, controls, hypotheses, statistical tests (chi-square, error bars), and AP-style scenario practice. Fully aligned with 2020 and 2025 CEDs. Exam-ready.

Independent Variable

A variable/item/something that is changed by researchers. In a cause-effect relationship, it's the "cause."

THINK: In mathematical terms, it's the X-Variable.

Dependent Variable

A variable/item/something to be measured/observed. In a cause-effect relation, it's the "effect."

THINK: In mathematical terms, it's the Y-variable.

Identify some examples of Independent & Dependent Variables

Example 1: Enzyme Activity (Unit #3)

IV: Temperature of the solution (what you change)

DV: Rate of enzyme reaction (measured by product formed or substrate used)

🌱 Example 2: Plant Growth (Unit #3)

IV: Amount of fertilizer applied to the plants

DV: Plant height after 2 weeks

☀️ Example 3: Photosynthesis Rate (Unit #3)

IV: Light intensity (distance of lamp from plant)

DV: Rate of oxygen production by the plant

Example 4: Bacterial Growth (Unit #6)

IV: Antibiotic concentration in growth medium

DV: Size of bacterial colonies after 24 hours

Example 5: Gene Expression (Unit #6)

IV: Presence or absence of a regulatory molecule (e.g., a repressor)

DV: Amount of mRNA transcribed (gene expression level)

Remembering Independent Variable vs Dependent Variable Trick

"I change the Independent, and the Dependent depends on it."

Mathematically, if X changes, Y will also change.

Constant

A constant is a factor kept the same across all experimental groups to ensure only the independent variable affects the outcome.

Ex. (1) Amount of water given to each plant (in a plant growth experiment); (2) Same species and age of organism used (in an enzyme or respiration experiment); (3) Light exposure duration (in a photosynthesis experiment); (4) Temperature of the environment (if not testing temperature itself); (5) Type and volume of growth medium (in a bacterial growth experiment)

Note...Constants are always kept the same in every experimental group.

Ex. If you're testing how light intensity affects photosynthesis:

Independent Variable: Light intensity (distance of lamp)

Dependent Variable: Oxygen production rate

Constants: (1) Same plant species; (2) Same size of plants; (3) Same soil type; (4) Same watering schedule; (5) Same room temperature; (6) Same number of hours of light exposure

THINK: ALWAYS KEPT THE SAME!

Experimental Control

The "normal" group used as a benchmark or point of comparison between experimental groups.

It helps determine if the independent variable is actually causing the observed effect.

Controls can be composed of:

(a) Positive Control: Group where a known response is expected (shows the experiment can detect an effect).

(b) Negative Control: Group where no response is expected (shows the baseline when no treatment is applied).

THINK: Benchmark of Comparision.

Positive Experimental Control

Group where a known response is expected (shows the experiment can detect an effect).

THINK: It will!

Negative Experimental Control

Group where no response is expected (shows the baseline when no treatment is applied).

THINK: It won't!

Null Hypothesis (H₀)

The outcome that will not happen. In AP Biology, it is generally phrased as, "There will be no statistically significant difference between ________."

Ex. If testing fertilizer on plants, the null hypothesis would be: "Fertilizer has no effect on plant growth."

THINK: Null = No real difference — just random chance.

Experimental/Alternative Hypothesis (Hₐ)

The outcome we predict/expect to see.

Ex. If testing fertilizer on plants, the experimental/alternative hypothesis would be..."Fertilizer has a significant effect on plant growth."

THINK: Experimental/Alternative = Yes difference - not random chance.

Investigative Question

How does (X) affect (Y)?

X = Independent Variable

Y = Dependent Variable

Standard Deviation (SD)

How spread out data is from the average (mean).

Stander Error of the Mean (SEM)

How much sample mean may vary if you took multiple samples from same population.

THINK: "Proof the more times we test something, the more reliable data we have!"

Describe the relationship between Standard Deviation & Standard Error of the mean

DIRECT RELATIONSHIP!

⬆️ Standard Deviation (SD) = ⬆️ Standard Error of the Mean (SEM)

95% Confidence Intervals/Error Bars

If you repeated your experiment 100x, 95% of the time the mean (avg.) would fall in that interval. We use error bars to tell if there is a statistically significant difference.

Note that it doesn't mean you're 95% confident in your data, but does mean that out of 100 times of doing the same experiment, 95/100 of those times would have a mean that would fall within that interval of the error bars.

Upper Limit = Mean + 2SEM

Lower Limit = Mean - 2SEM

What does it mean when error bars overlap?

If error bars overlap, there is no statistically significant difference. We must FAIL TO REJECT the null hypothesis.

THINK:

✅ Error Bars DO Overlap

❌ Statistically Significant Difference

➡️ FAIL TO REJECT H₀ (Null Hypothesis)

What does it mean when error bars do NOT overlap?

If error bars do not overlap, there is a statistically significant difference, we must reject the null hypothesis.

THINK:

❌ Error Bars do NOT Overlap

✅ Statistically Significant Difference

➡️ REJECT H₀ (Null Hypothesis)

Differentiate between what it means to fail to reject the H₀ and reject the H₀

Fail to reject H₀ = No statistically significant difference.

Reject H₀ = Statistically significant difference.

What is the purpose of a chi-square test in AP Biology experiments?

This is a question related to Unit #5, generally not taught in Unit #1.

The chi-square test determines whether observed data are significantly different from expected data. It helps evaluate if differences are due to random chance or another factor.

THINK: "Statistical analysis that proves it's close enough."

State the formula for chi-square (χ2)

This is a question related to Unit #5, generally not taught in Unit #1.

χ2 = ∑((o-e)²/e)

where...

χ2 = Chi-Square Value

∑ = Sum of All

o = observed

e = expected

How do you calculate degrees of freedom (df) in a chi-square test?

This is a question related to Unit #5, generally not taught in Unit #1.

df = # of possible outcomes/categories - 1

Use the AP Biology Formula Sheet: What is the critical value for chi-square at df = 1 and p = 0.05?

This is a question related to Unit #5, generally not taught in Unit #1.

CV = 3.84

P-value

This is a question related to Unit #5, generally not taught in Unit #1.

The probability of getting this large of a difference by random chance. Given on the AP exam. If there is no p-value provided, assume a p-value of 0.05.

Evaluate the hypothesis, given that χ2 < Critical Value.

This is a question related to Unit #5, generally not taught in Unit #1.

Since χ2 < CV, we must FAIL TO REJECT the null hypothesis.

THINK: χ2 < CV → Fail to Reject NULL HYPOTHESIS

Evaluate the hypothesis, given that χ2 ≥ Critical Value

This is a question related to Unit #5, generally not taught in Unit #1.

Since χ2 ≥ CV, we must REJECT the null hypothesis.

THINK: χ2 ≥ CV → REJECT NULL HYPOTHESIS

What does it mean to fail to reject the null hypothesis in a chi-square test?

This is a question related to Unit #5, generally not taught in Unit #1.

It means that the observed and expected results are close enough that differences are likely due to random chance.No statistically significant difference.

THINK: χ2 < CV → Fail to reject the null nypothesis

What does it mean to reject the null hypothesis in a chi-square test?

This is a question related to Unit #5, generally not taught in Unit #1.

It means the differences between observed and expected results are too large to be explained by random chance.Statistically significant difference exists.

THINK: χ2 ≥ CV → Reject the null nypothesis

What is the null hypothesis for a genetic cross (e.g., 3:1 ratio)?

This is a question related to Unit #5, generally not taught in Unit #1.

The observed offspring ratios will not differ significantly from the expected 3:1 Mendelian ratio. Any differences are due to random chance.

How do you identify observed (O) and expected (E) values in AP Biology multiple-choice questions?

Observed (O): The numbers collected or recorded from an experiment. Look for words like "measured," "recorded," "observed," or "data collected."

Expected (E): The numbers calculated based on predictions, models, ratios, or hypotheses. Look for phrases like "expected ratio," "theoretical value," or "model predicts."

THINK: If you saw it happen, it's Observed. If you predicted it would happen, it's Expected.

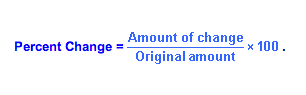
Skill/Scenario Practice: A scientist tests how different amounts of sunlight affect the rate of photosynthesis in spinach plants by measuring the amount of oxygen produced. Identify the following: (a) The independent variable (IV); (b) The dependent variable (DV).

(a) Independent Variable (IV): Amount of sunlight

(b) Dependent Variable (DV): Rate of oxygen production (photosynthesis)

Skill/Scenario Practice: In a study comparing two antibiotics, the error bars for bacterial colony size overlap between the two treatments. Based on the error bars, what conclusion should be drawn about the effectiveness of the antibiotics?

Because the error bars overlap, there is likely no statistically significant difference between the effectiveness of the two antibiotics. Fail to reject the null hypothesis.

Skill/Scenario Practice: A chi-square value of 2.7 is calculated for a genetics experiment testing a 3:1 Mendelian ratio.(Assume df = 1, critical value = 3.84 at p=0.05.) Should the null hypothesis be rejected or failed to be rejected? Justify your answer.

This is a question related to Unit #5, generally not taught in Unit #1.

Decision: Fail to reject the null hypothesis.

Justification: The chi-square value (2.7) is less than the critical value (3.84), meaning the observed differences are likely due to random chance as χ2 < CV → Fail to reject the null hypothesis (no significant difference).

Skill/Scenario Practice: A genetic cross yields a chi-square value of 5.2. Assume the degrees of freedom (df) = 1. Critical value at p = 0.05 = 3.84.

Based on this information, should the null hypothesis be rejected or failed to be rejected? Justify your answer.

This is a question related to Unit #5, generally not taught in Unit #1.

Reject the null hypothesis as χ2 ≥ CV → Reject the H₀.

We are given that χ2 = 5.2 and CV = 3.84. Thus, χ2 > CV, meaning we must reject the null hypothesis as the results are statistically significant.

Skill/Scenario Practice: A chi-square value of 0.9 is calculated in an experiment with two possible outcomes (df = 1). No critical value is given.

Evaluate whether the observed and expected results are likely significantly different or not.

This is a question related to Unit #5, generally not taught in Unit #1.

The chi-square value (0.9) is very small.

This suggests the observed results are close to expected and differences are likely due to random chance.

Conclusion: No statistically significant difference. Likely fail to reject the null hypothesis.

THINK: Small chi-square? Small difference. Stay with the null. Fail to reject the null hypothesis.

Chi-Square Size Interpretation:

Small χ2 = Observed ≈ Expected → Fail to reject

Large χ2 = Observed far ≠ Expected → Reject