Lecture 11 Transformers

What kind of data can transformers handle

all kinds of data, image, video, text, etc. super powerful for answering MLP related problems

Encoder - used for classification, feature extraction

Decoder - used for text generation LLM stuff

token

token - chunk of text

common/short words = one token just depends on dictionary

long less common words = multiple tokens

byte-pair encoding (BPE)

byte pair encoding

starts with character level vocab and starts iteratively merging frequent pairs into new tokens until desired vocab size reached

frequent pairings matched in frequency tables ~30-100k words

token input

each token is a one hot vector [nxN]

• the one is in the position of the index in the dictionary (token ID)

token vector

vector of each token ID of the input in its order

(token ID is the index in the dictionary)

Transformer

encoder + decoder + self attention

autoregressive model

• n tokens in, one token out

  • output used as part of next iteration input

probabilistic

• uses (softmax) to return a probability distribution of possible tokens and outputs the highest probable output

Self attention - basic parts

Data tensor X [n x N]→

(in practice data is 3D with [ _ x _ x B]

(batch size) Determined through back propagation

• Query Q (what' I’m looking for)

  • Q = W_QX [n x d_Q ]

• Key K (what I contain)

  • K = W_KX [n x d_K]

• Value V (actual content of X that will be passed forward)

  • V = W_VX [n x d_V]

• W = linear projection [N x d_{{K, Q, V}}](transformations) learned so each Q,K,V are different

notations

n = # of tokens

N = dictionary size

hyperparameters

d = embedding size (dimension size? used for the QKV) (larger d means more information from the token )

H = # of attention heads (similar to # of filters in CNN)

Self-attention operations

1. Compute scores between different input vectors S = Q ^. K^T [n x n]

   1. in smoothie ex these is how much u like the fruit

2. Add mask

3. Normalize the scores for the stability of gradient S_n= S/sqrt(d_k) [n x n] d_k = embedding size

4. Apply softmax to translate the scores into probabilities (attention weights) P = softmax(S_n) [n x n]

   1. P is the correlation matrix of the input tokens [0, 1] bc of softmax

5. Obtain the weighted value matrix with Z = V * P [n x d]

   1. important bc it integrates only most relevant parts of context for each token, eliminating unfiltered noise

Self-attention masking

Need to add padding to get to max length of input, and need to mask padding so not considered in calculations

Add before normalizing or applying softmax

• matrix of -infinity for padding tokens (becomes 0 in softmax)

• 0 for actual inputs

Multi-head attention (MHA)

allows for attention between multiple words

MHA output [n x dH] - attention for each token

• basically dH # of self attention concatenated together (each with diff QKV)

• each self attention head gets a diff dimension (feature) and so its not redundant and analyzing the same data

Transformer architecture

input —> embedding + position encoding → encoder stack → decoder → linear → softmax → output

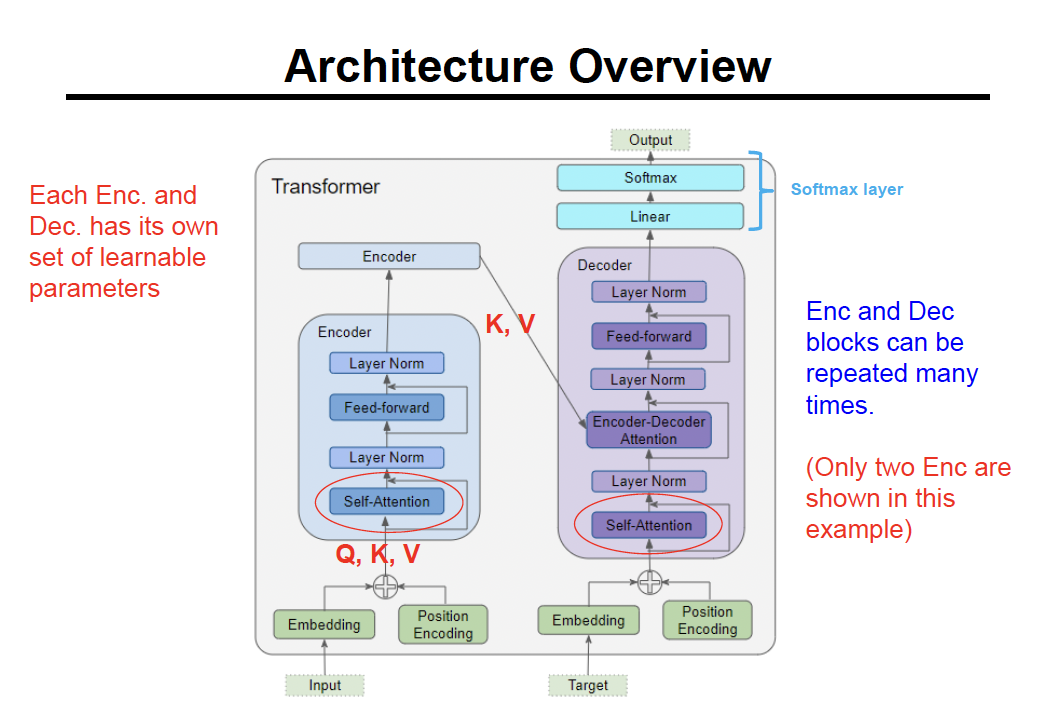
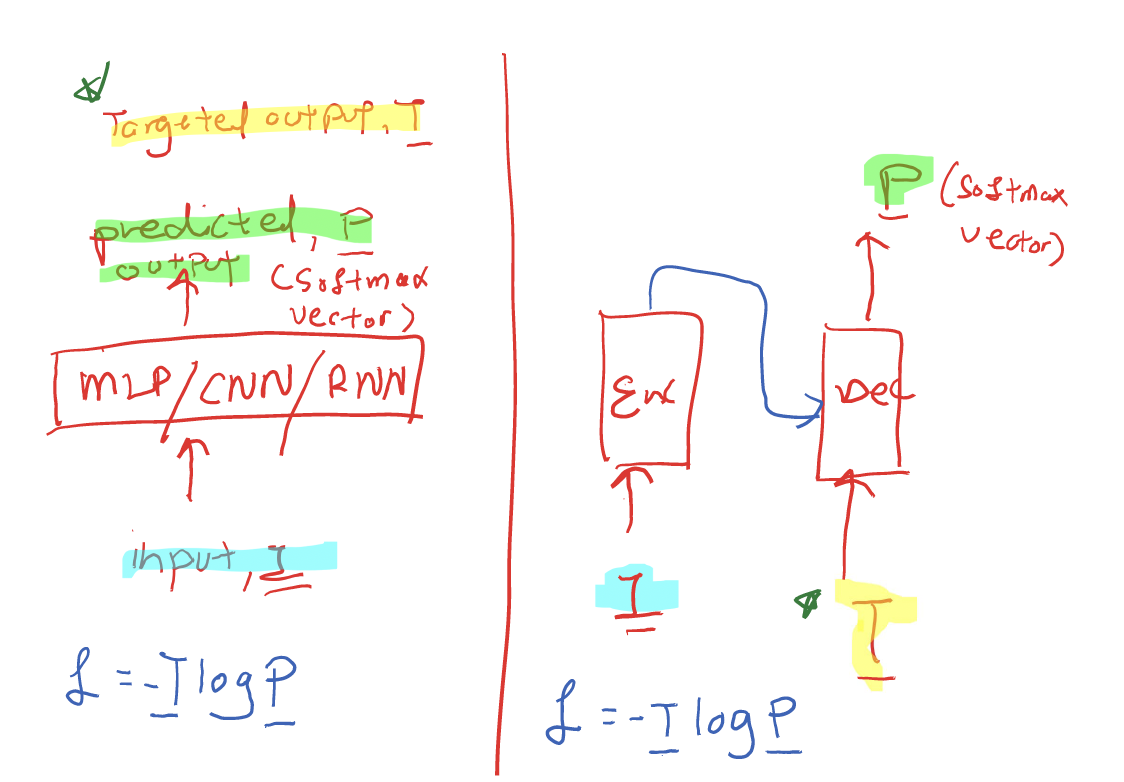
How input / output works in transformers

all input, one out, then out becomes new input

still minimize loss (cross-entropy) but the target output is not isolated and instead included in the input unlike other models

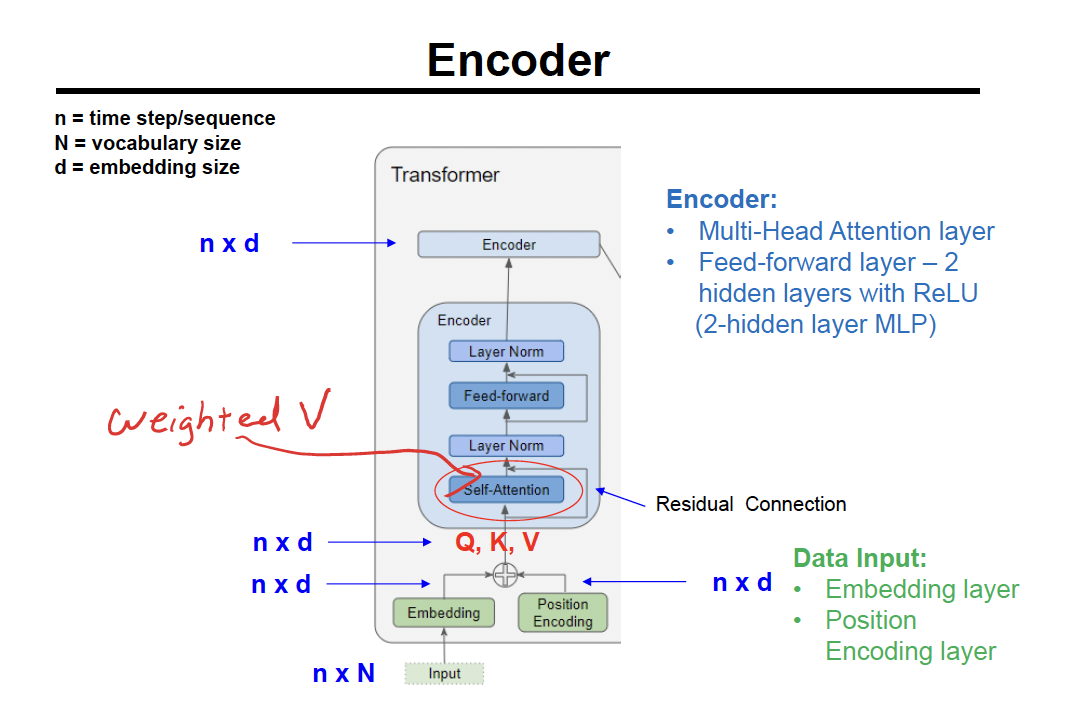
Encoder

input →

embedding + position encoding →

self - attention (produces weighted V) → residual connection (skip connection) →

layer norm →

feed forward →

• 2 hidden layers with ReLU (2-hidden layer MLP)

layer norm → decoder

Layer normalization

variant of batch normalization

• normalizes using mean and std row by row instead of whole matrix

• when dividing by std also add 0.0001 to avoid overflow

Input embedding

converts raw data (one-hot vector) → embedding

encodes the meaning of the words

linear projection module

Sinusoidal position encoding

k = hyperparameter controlling frequency range

larger = smoother but less informative encodings

d = encoding dimension

pt is corresponding encoding

sin(w* t) if even

cos(wk *t) if odd

w = 1/1000^2k/d

Decoder attention

utilizes cross attention - not the same as attention used in encoder

helps combine input and target sequence

• target language Q

• input language K and V

triangular masking for n tokens in one token out (auto reg nature)

greedy decoding from softmax, just choose highest probability, get the Token ID (dictionary index) and the token itself