Chi Square Test

Parametric Tests

• make assumptions about the distribution of data

• assumptions are key to the ideas behind things like t-tests and ANOVA

What conditions are required for parametric tests

• continuous data

• normally distributed

• similar variances

• large enough sample sizes

Parametric Tests

• make assumptions about the distribution of data

• assumptions are key to the ideas behind things like t-tests and ANOVA

What conditions are required for parametric tests

• continuous data

• normally distributed

• similar variances

• large enough sample sizes

Nonparametric Tests

• do not use the same assumptions

• sometime it uses counts which cannot be

  • continuous

  • normally distributes

  • have variance

What is the most common nonparametric test

CHI SQUARE TEST

Why is the Chi Square Test a nonparametric test

• compares frequencies of different groups

What is the Chi Square (x²) test

• is the distribution of these groups different than what we would expect is variable of interest truly random

• Chi Square approximates the overall size of the difference

• This is determined by comparing the expected data to the actual data

Null Hypothesis (4 groups)

Null: G1 = G2 = G3 = G4

Research Hypothesis (4 groups)

Research: G1 ≠ G2 ≠ G3 ≠ G4

How to set up the Chi Square test

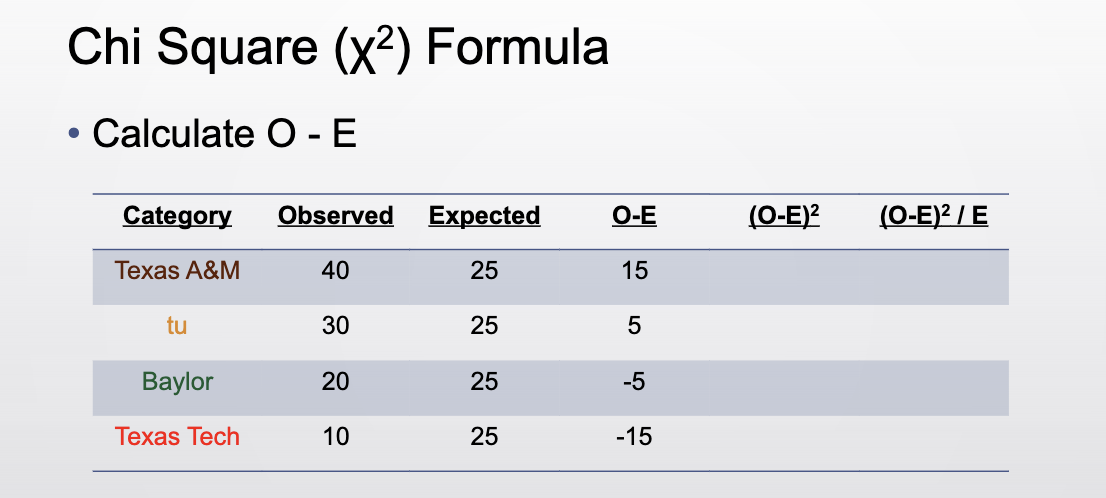
How do you interpret a:

CV = 7.82

x² = 20

• reject the null

• interpretation: the distribution across the groups is not equal

What report when reporting a chi square test

• The x² and what it tells us

• report degree of freedom

• what does the obtained value tell us

• what doe the p value tell us

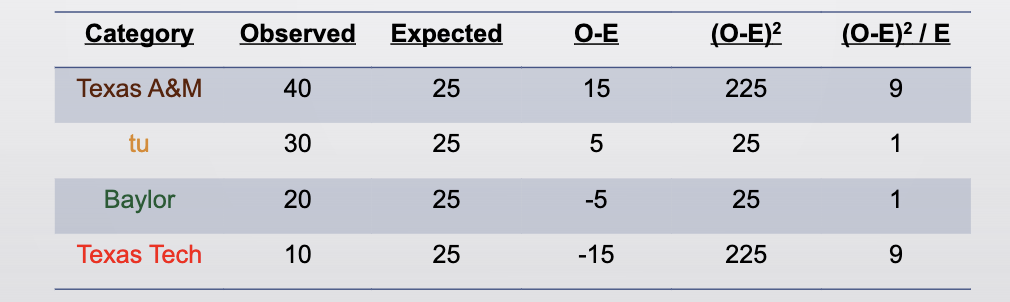
Write a report for this example:

• x² = 20

• CV = 7.82

A chi square test revealed a difference in college
preference among high school seniors in Texas, χ2(3) =
20, p < .05. More students favored Texas A&M (40%) than
any other school, with the University of Texas the second
most popular school (30%), followed by Baylor (20%) and
Texas Tech (10%).