Dinámica: Leyes de Newton y Aplicaciones

https://chatgpt.com/c/68378d79-bbf4-800c-becd-ca8df0be0fb4

¿Qué es una fuerza?

Es un empuje o arrastre que cambia o tiende a cambiar el estado de movimiento de un objeto; es un vector con magnitud y dirección

¿Qué es masa?

Es la medida de la inercia de un objeto, o la cantidad de materia que posee, y se mide en kilogramos en el sistema internacional

¿Qué es peso?

Es la fuerza de gravedad que actúa sobre un objeto de masa m, calculada como P=mg, donde g es la aceleración de la gravedad

¿Qué es la fuerza normal?

Es la fuerza perpendicular que ejerce una superficie sobre un objeto en contacto, igual y opuesta a la componente perpendicular de otras fuerzas

¿Qué establece la primera ley de Newton?

Afirma que un objeto permanecerá en reposo o en movimiento rectilíneo uniforme a menos que una fuerza neta actúe sobre él

¿Qué expresa la segunda ley de Newton?

Indica que la fuerza neta sobre un objeto es igual al producto de su masa por su aceleración, F=ma

¿Cuál es el principio de la tercera ley de Newton?

Establece que a cada acción corresponde una reacción igual en magnitud y opuesta en dirección entre dos objetos que interactúan

¿Qué es un diagrama de cuerpo libre?

Es un gráfico que representa todas las fuerzas aplicadas sobre un objeto como vectores que parten de un punto único

¿Cuáles son los pasos del enfoque general para resolver problemas con las leyes de Newton?

Leer el problema, dibujar un diagrama de cuerpo libre, descomponer fuerzas en componentes, aplicar F=ma en cada eje y resolver las ecuaciones resultantes

¿Cómo se define la fricción cinética?

Es la fuerza que se opone al deslizamiento de dos superficies ya en movimiento, dada por F_{\rm fr}=µ_kF_N

¿Cómo se define la fricción estática?

Es la fuerza que impide el inicio del movimiento entre dos superficies en reposo, con F_{\rm fr}\le µ_sF_N

¿En qué se diferencian los coeficientes de fricción estática y cinética?

Generalmente µ_s>µ_k, lo que indica que se requiere más fuerza para iniciar el movimiento que para mantenerlo

¿Qué caracteriza el movimiento circular uniforme?

Es el movimiento de un objeto en un círculo de radio constante con rapidez constante, cambiando solo la dirección de la velocidad

¿Cómo se calcula la aceleración centrípeta?

Se expresa como a_c=\frac{v^2}{r} y siempre apunta hacia el centro del círculo

¿Qué diferencia al movimiento circular no uniforme del uniforme?

En el no uniforme la rapidez varía y aparece una aceleración tangencial además de la centrípeta

¿Qué sucede en una curva de carretera sin peralte?

El vehículo depende de la fricción estática de los neumáticos contra la carretera para generar la fuerza centrípeta necesaria

¿Qué ventajas ofrece una curva peraltada?

La componente horizontal de la fuerza normal suministra el centrípeta sin necesidad de fricción, aumentando la seguridad a cierta velocidad de diseño

¿Qué es la fuerza de arrastre en un fluido?

Es una fuerza dependiente de la velocidad que se opone al movimiento, siendo proporcional a v a bajas velocidades y a v^2 a altas velocidades

¿Qué es la velocidad terminal?

Es la rapidez constante que alcanza un objeto cuando la fuerza de arrastre equilibra su peso, resultando en aceleración neta cero

¿Qué son los vectores en física?

Son magnitudes que incluyen tanto módulo como dirección, utilizadas para representar fuerzas, velocidades y desplazamientos

¿Cómo expresa el SI las magnitudes de masa y fuerza?

La masa se mide en kilogramos (kg) y la fuerza en newtons (N), donde 1\ \mathrm{N}=1\ \mathrm{kg\cdot m/s^2}

¿Qué valor se usa para la aceleración de la gravedad?

Se suele tomar g=9.8\ \mathrm{m/s^2} como aproximación de la aceleración gravitatoria en la superficie terrestre

¿Qué es el coeficiente de arrastre y cómo se relaciona con la fuerza de arrastre?

El coeficiente de arrastre C_d es un factor adimensional que caracteriza la resistencia de un objeto al flujo; la fuerza de arrastre se calcula como F_d=\tfrac12,C_d,\rho,A,v^2

¿Qué es el número de Reynolds y por qué importa en la dinámica de fluidos?

Es la relación adimensional Re=\tfrac{\rho v L}{\mu} que indica si el flujo es laminar o turbulento, afectando la forma de la curva de resistencia

¿Cómo varía la fricción estática en una superficie inclinada?

El máximo de fricción estática es F_{fr,\max}=µ_s,m,g,\cos\theta y se activa antes de deslizar; al aumentar el ángulo \theta, la componente normal disminuye y con ello el umbral de fricción

¿Cómo se determina el ángulo de peralte de diseño para una curva?

Se utiliza \tan\phi=\tfrac{v^2}{r,g} para que la componente horizontal de la normal suministre la fuerza centrípeta sin depender de la fricción

¿Qué aceleraciones aparecen en el movimiento circular no uniforme?

Aceleración centrípeta a_c=\tfrac{v^2}{r} dirigida al centro y aceleración tangencial a_t=\tfrac{dv}{dt} que altera la rapidez

¿Cuál es el procedimiento para elegir sistema de ejes en un diagrama de cuerpo libre?

Se eligen ejes alineados con direcciones de interés (por ejemplo paralelo y perpendicular a un plano) para simplificar la descomposición de fuerzas

¿Cómo afecta la densidad del fluido a la velocidad terminal?

La velocidad terminal v_t cumple mg=\tfrac12C_d\rho A v_t^2, de modo que al aumentar \rho disminuye v_t por mayor resistencia

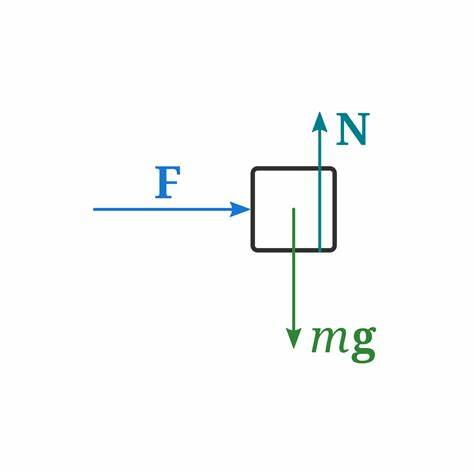
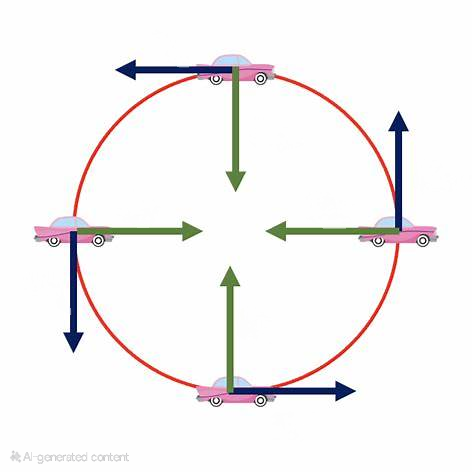
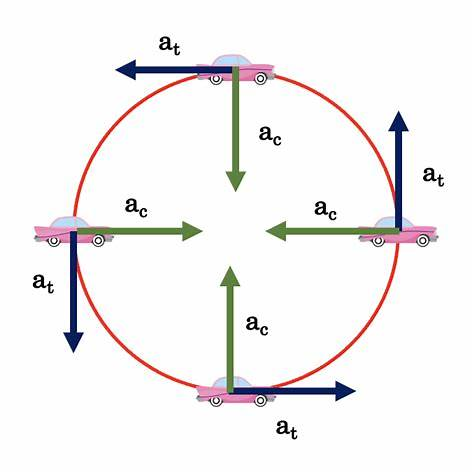
(I) ¿Qué fuerza se necesita para acelerar a un niño en un trineo (masa total m = 55\ \mathrm{kg}) con una aceleración de a = 1{,}4\ \mathrm{m/s^2}?

77\ \mathrm{N}

(I) ¿Cuál es el peso de un astronauta de 68\ \mathrm{kg}

• (a) en la Tierra (g = 9{,}8\ \mathrm{m/s^2})
  
  

• (b) en la Luna (g = 1{,}7\ \mathrm{m/s^2})
  
  

• (c) en Marte (g = 3{,}7\ \mathrm{m/s^2})
  
  

• (d) en el espacio exterior viajando con velocidad constante?

(a) 666{,}4\ \mathrm{N}
(b) 115{,}6\ \mathrm{N}
(c) 251{,}6\ \mathrm{N}
(d) 0\ \mathrm{N}

(II) Estima la fuerza media que ejerce un lanzador de peso sobre un proyectil de 7{,}0\ \mathrm{kg} si el proyectil se mueve 2{,}8\ \mathrm{m} y se lanza con velocidad de 13\ \mathrm{m/s}.

2{,}1\times10^2\ \mathrm{N} aproximadamente.

(II) ¿Qué fuerza media se necesita para acelerar un proyectil de 9{,}20\ \mathrm{g} desde el reposo hasta 125\ \mathrm{m/s} en un recorrido de 0{,}800\ \mathrm{m} dentro del cañón de un rifle?

F_{\mathrm{media}} = \frac{0.00920\ \mathrm{kg}\,(125\ \mathrm{m/s})^2}{2 \times 0.800\ \mathrm{m}} \approx 8.98\times10^{1}\ \mathrm{N}

Por tanto, la fuerza media es aproximadamente 9.0\times10^1\;N .

(I) Una caja que pesa 77{,}0\ \mathrm{N} reposa sobre una mesa. Una cuerda atada a la caja pasa verticalmente sobre una polea y cuelga un peso en el otro extremo (Fig. 4–33). Determina la fuerza que ejerce la mesa sobre la caja si el peso colgado pesa

(a) 30{,}0\ \mathrm{N}

(b) 60{,}0\ \mathrm{N}

(c) 90{,}0\ \mathrm{N}

(a) 47 N

(b) 17 N

(c) 0 N

(II) Una limpiadora de ventanas se eleva tirando de sí misma usando el sistema cubeta–polea que se muestra en la Fig. 4–36.

(a) ¿Con qué fuerza debe tirar hacia abajo para elevarse lentamente a velocidad constante?

(b) Si aumenta esa fuerza en un 15 %, ¿cuál será su aceleración?

La masa de la persona más la cubeta es 72\ \mathrm{kg}.

(a) T = \frac{mg}{2} = \frac{72\cdot9.8}{2} = 352.8\ \mathrm{N}
(b) a = 0.15,g = 0.15\cdot9.8 = 1.47\ \mathrm{m/s^2}

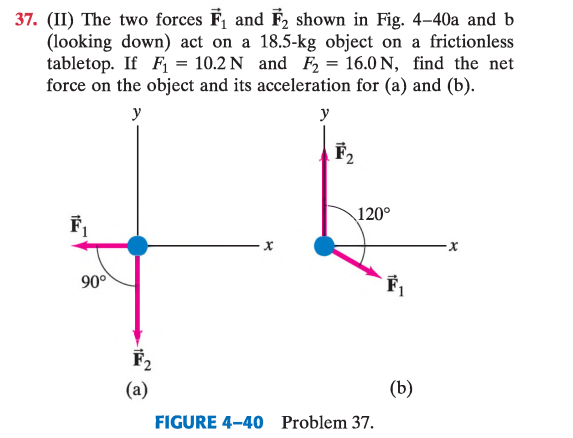
(II) Las dos fuerzas \vec{F}_1 y \vec{F}_2 mostradas en la Fig. 4–40 (a) y (b) (vista desde arriba) actúan sobre un objeto de 18{,}5\ \mathrm{kg} en una mesa sin fricción. Si F_1 = 10{,}2\ \mathrm{N} y F_2 = 16{,}0\ \mathrm{N}, encuentra la fuerza neta sobre el objeto y su aceleración para

(a) la configuración de la Fig. 4–40 (a)

(b) la configuración de la Fig. 4–40 (b)

(a) |\vec F_{\rm net}|=\sqrt{(-10.2)^2+(-16.0)^2}=18.97\ \mathrm N,\quad a=\frac{18.97}{18.5}=1.03\ \mathrm{m/s^2}

(b)F_{1x}=10.2\cos(-30^\circ)=8.84\ \mathrm N,\ F_{1y}=10.2\sin(-30^\circ)=-5.10\ \mathrm N,\ F_{{\rm net},x}=8.84\ \mathrm N,\ F_{{\rm net},y}=16.0-5.10=10.9\ \mathrm N\implies|\vec F_{\rm net}|=\sqrt{8.84^2+10.9^2}=14.03\ \mathrm N,\quad a=\frac{14.03}{18.5}=0.76\ \mathrm{m/s^2}

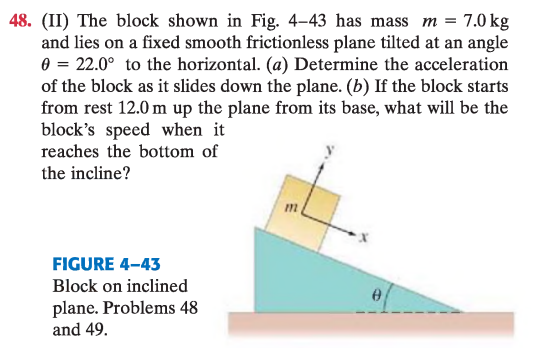
(II) El bloque de la Fig. 4–43 tiene masa m = 7{,}0\ \mathrm{kg} y está sobre un plano inclinado fijo, liso y sin fricción, con ángulo \theta = 22{,}0^\circ respecto a la horizontal.

(a) Determina la aceleración del bloque mientras se desliza por el plano.

(b) Si parte del reposo a 12{,}0\ \mathrm{m} por encima de la base, ¿cuál será su velocidad al llegar al fondo?

(a) a=g\sin\theta=9.8\sin22^{\circ}=3.67\ m/s^2

(b)v=\sqrt{2as}=\sqrt{2(3.67)(12.0)}=9.39\ m/s

(II) La Fig. 4–45 muestra un bloque (masa m_A) sobre una superficie horizontal lisa, unido por una cuerda que pasa por una polea a un segundo bloque (m_B) que cuelga verticalmente.

(a) Dibuja un diagrama cuerpo-libre para cada bloque, indicando la fuerza de gravedad, la tensión de la cuerda y la fuerza normal.

(b) Aplica la segunda ley de Newton para obtener fórmulas de la aceleración del sistema y de la tensión en la cuerda. Ignora la fricción y las masas de la polea y la cuerda.

(a) FBD:

* Bloque A: T hacia la derecha.

* Bloque B: m\_Bg hacia abajo y T hacia arriba.

(b)

a=\frac{m_B\,g}{m_A+m_B},\quad T=\frac{m_A\,m_B\,g}{m_A+m_B}

(II)

(a) Si m_A = 13{,}0\ \mathrm{kg} y m_B = 5{,}0\ \mathrm{kg} en la Fig. 4–45, determina la aceleración de cada bloque.

(b) Si inicialmente m_A está en reposo a 1{,}250\ \mathrm{m} del borde de la mesa, ¿cuánto tarda en llegar al filo si el sistema se deja moverse libremente?

(c) Si m_B = 1{,}0\ \mathrm{kg}, ¿qué valor debe tener m_A para que la aceleración del sistema sea \tfrac{1}{100}g?

(a) a=\frac{m\_Bg}{m\_A+m\_B}=\frac{5.0\cdot9.8}{13.0+5.0}=2.72\ \mathrm{m/s^2}

(b) t=\sqrt{\frac{2s}{a}}=\sqrt{\frac{2\cdot1.250}{2.72}}=0.96\ \mathrm{s}

(c) a=0.1g\implies m\_A=\frac{m\_Bg}{0.1g}-m\_B=\frac{1.0\cdot9.8}{0.98}-1.0=9.0\ \mathrm{kg}

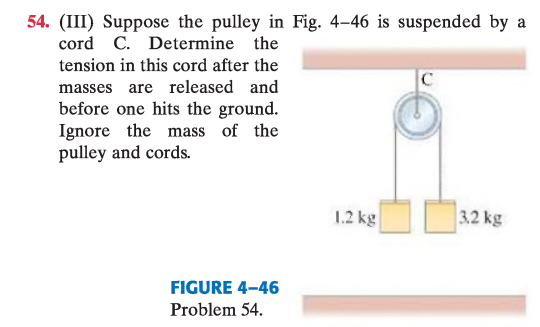
(III) Suponga que la polea de la Fig. 4–46 está suspendida de una cuerda C. Determine la tensión en esta cuerda después de que se liberan las masas y antes de que una de ellas toque el suelo. Ignore la masa de la polea y de las cuerdas.

T = m\_1\Bigl(g + \frac{(m\_2 - m\_1),g}{m\_1 + m\_2}\Bigr)=1.2\bigl(9.8+\tfrac{(3.2-1.2),9.8}{3.2+1.2}\bigr)=17.1\ \mathrm N,\quad T\_C=2T=34.2\ \mathrm N

(III) Las dos masas mostradas en la Fig. 4–50 están inicialmente a 1{,}8\ \mathrm{m} sobre el suelo, y la polea sin masa y sin fricción está a 4{,}8\ \mathrm{m} de altura. ¿Qué altura máxima alcanza el objeto más ligero después de liberar el sistema?

[Pista: Primero determine la aceleración de la masa más ligera y luego su velocidad en el momento en que la masa más pesada golpea el suelo. Ésta es su velocidad de “lanzamiento”. Suponga que la masa no golpea la polea. Ignore la masa de la cuerda.]

a=\frac{(3.6-2.2)g}{3.6+2.2}=2.37\ \mathrm{m/s^2},\quad v=\sqrt{2as}=\sqrt{2(2.37)(1.8)}=2.92\ \mathrm{m/s},\quad H_{\max}=2s+\frac{v^2}{2g}=4.03\ \mathrm{m}

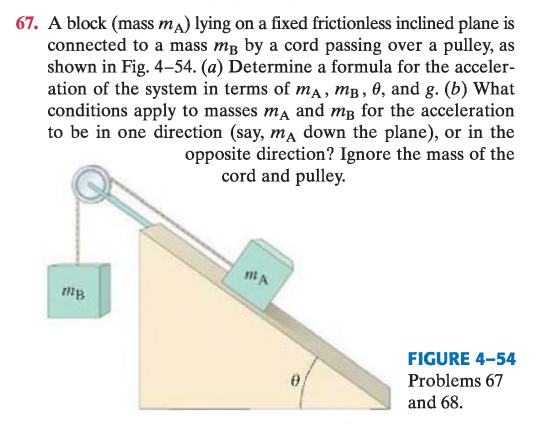
Un bloque (masa m_A) yace sobre un plano inclinado fijo y sin fricción, conectado a una masa m_B por una cuerda que pasa sobre una polea, como muestra la Fig. 4–54.

(a) Determine una fórmula para la aceleración del sistema en términos de m_A, m_B, \theta y g.

(b) ¿Qué condiciones deben cumplir m_A y m_B para que la aceleración sea en una dirección dada (por ejemplo, m_A bajando por el plano), o en la dirección opuesta? Ignore la masa de la cuerda y de la polea.

(a) a=\frac{m_A,g\sin\theta - m_B,g}{m_A + m_B}
(b) a>0\iff m_A\sin\theta>m_B,\quad a<0\iff m_A\sin\theta<m_B,\quad a=0\iff m_A\sin\theta=m_B

(I) Si el coeficiente de fricción cinética entre un cajón de 22\ \mathrm{kg} y el piso es \mu_k=0{,}30, ¿qué fuerza horizontal se requiere para mover el cajón a velocidad constante? ¿Qué fuerza se requiere si \mu_k=0?

(a) F=\mu_kmg=0.30\cdot22\cdot9.8=64.7\ \mathrm N
(b) F=0

(I) ¿Cuál es la aceleración máxima que puede tener un automóvil si el coeficiente de fricción estática entre los neumáticos y el pavimento es \mu_s = 0.90?

a_{\max}=\mu_s,g=0.90\times9.8=8.82\ \mathrm{m/s^2}

En la Fig. 5-35 el coeficiente de fricción estática entre la masa m_A y la mesa es 0.40, mientras que el coeficiente de fricción cinética es 0.30 y la masa colgante es m_B=2.0\ \mathrm{kg}.

(a) ¿Qué valor mínimo de m_A evitará que el sistema empiece a moverse?

(b) ¿Qué valor(es) de m_A mantendrá(n) el sistema en movimiento a velocidad constante?

(a) m_A\ge\frac{m_B}{\mu_s}=\frac{2.0}{0.40}=5.0\ \mathrm{kg}

(b) m_A=\frac{m_B}{\mu_k}=\frac{2.0}{0.30}=6.67\ \mathrm{kg}

27. (II) Un paquete de masa m se deja caer verticalmente sobre una cinta transportadora horizontal cuya velocidad es v = 1.5\ \mathrm{m/s}, y el coeficiente de fricción cinética entre el paquete y la cinta es \mu_k = 0.70.

(a) ¿Cuánto tiempo desliza el paquete sobre la cinta (hasta que esté en reposo relativo a la cinta)?

(b) ¿Qué distancia recorre el paquete durante ese tiempo?

(a) Tiempo hasta igualar la velocidad de la banda:

t = \frac{v}{\mu_k\,g}

t = \frac{1.5}{0.70 \times 9.8} \approx 0.22\ \mathrm{s}

(b) Distancia recorrida durante ese tiempo:

x = \frac{v^2}{2\,\mu_k\,g}

x = \frac{(1.5)^2}{2 \times 0.70 \times 9.8} \approx 0.16\ \mathrm{m}

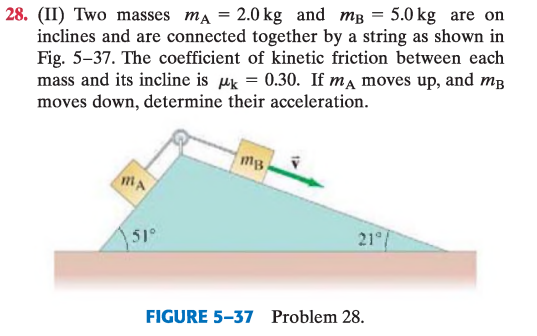
Dos masas m_A = 2.0\ \mathrm{kg} y m_B = 5.0\ \mathrm{kg} están sobre planos inclinados y están conectadas por una cuerda como se muestra en la Fig. 5–37. El coeficiente de fricción cinética entre cada masa y su plano es \mu_k = 0.30. Si m_A se mueve hacia arriba y m_B hacia abajo, determine su aceleración.

a = \frac{5g\sin21^\circ -0.3\cdot5g\cos21^\circ -2g\sin51^\circ -0.3\cdot2g\cos51^\circ}{2+5} = -2.16\ \mathrm{m/s^2} (mₐ desliza hacia abajo, |a|=2.16 m/s²)

¿Cuál es la velocidad máxima con la que un automóvil de 1200\ \mathrm{kg} puede tomar una curva de radio 80{,}0\ \mathrm{m} en una carretera plana si el coeficiente de fricción entre los neumáticos y el pavimento es 0{,}65? ¿Es este resultado independiente de la masa del automóvil?

v_{\max}=\sqrt{\mu_s,g,r}=\sqrt{0.65\cdot9.8\cdot80.0}=22.6\ \mathrm{m/s} , independiente de m.

¿A qué velocidad de rotación (en rpm) debe girar una centrífuga para que una partícula situada a 8.00\ \mathrm{cm} del eje de rotación experimente una aceleración de 1.25\times10^5,g?

\omega=\sqrt{\frac{125000,g}{0.08}}=\sqrt{\frac{125000\cdot9.8}{0.08}}=3.91\times10^3\ \mathrm{rad/s}

f=\frac{\omega}{2\pi}=\frac{3.91\times10^3}{2\pi}=6.23\times10^2\ \mathrm{Hz}

\mathrm{rpm}=f\times60=6.23\times10^2\cdot60=3.74\times10^4\ \mathrm{rpm}

En una pista de hielo, dos patinadores de igual masa se toman de las manos y giran en un círculo común una vez cada 2{,}5\ \mathrm{s}. Si sus brazos miden 0{,}80\ \mathrm{m} cada uno y cada patinador tiene masa 60{,}0\ \mathrm{kg}, ¿qué fuerza ejercen entre sí?

F=m\omega^2r=60.0!\left(\frac{2\pi}{2.5}\right)^{2}(0.80)=3.03\times10^2\ \mathrm{N}