CS 245 Multiple Choice

The formulas p and \neg \neg p are

semantically equivalent but not syntactically equal

Let A be the propositional formula p \to (\neg p). Then A is

satisfiable but not a tautology

Let A be the propositional formula (p\land \neg p)\to(\neg q) . Then A is

a tautology

Let A \in \text{Form}(\mathcal{L}^p). If A is a contradiction, then A is ____ satisfiable

never

Let A \in \text{Form}(\mathcal{L}^p). If A is satisfiable, then A is ____ a tautology

sometimes

Let \Sigma \subseteq \text{Form}(\mathcal{L}^p). Let t be a truth valuation. If \Sigma^t =1, then \Sigma is ___ satisfiable

always

Let t be a truth valuation. Then \emptyset^t = 1 ___ holds

always

Let \Sigma \subseteq \text{Form}(\mathcal{L}^p). Let A \in \text{Form}(\mathcal{L}^p). If \Sigma is unsatisfiable, then \Sigma \vDash \neg A ___ holds

always

Let \Sigma \subseteq \text{Form}(\mathcal{L}^p). Let A \in \Sigma and B \in \Sigma. If \Sigma is unsatisfiable, then \emptyset \vDash A \land B ___ holds

sometimes

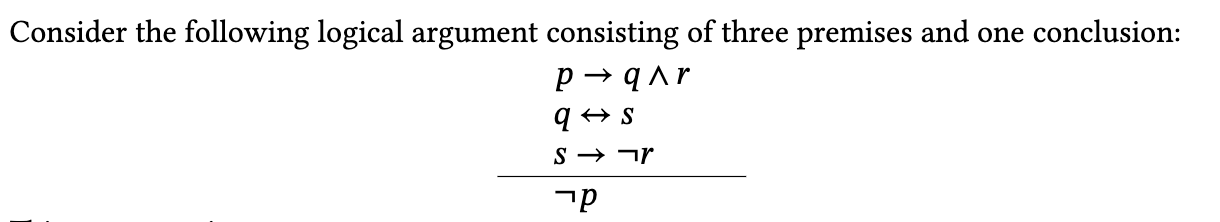
This argument is

valid

Let A \in \text{Form}(\mathcal{L}^p). Let \Sigma \subseteq \text{Form}(\mathcal{L}^p). If \Sigma \cup \{ \neg A \} is inconsistent, then \Sigma \vDash A ___ holds

always

Let A,B,C \in \text{Form}(\mathcal{L}^p). Then the set \{ \neg(A \to B), \neg B \to C, A \to \neg C \} is ____ a consistent set of formulas

never

Let \Sigma \subseteq \text{Form}(\mathcal{L}^p). Let A \in \text{Form}(\mathcal{L}^p). If \Sigma \vdash B, then \Sigma \cup \{ A \} \vdash B ___ holds

always

Let \Sigma \subseteq \text{Form}(\mathcal{L}^p). Let A \in \text{Form}(\mathcal{L}^p). If \Sigma, A \vdash B, then \Sigma \vdash B ___ holds

sometimes

Let \Sigma_1, \Sigma_2 \subseteq \text{Form}(\mathcal{L}^p). Let A \in \text{Form}(\mathcal{L}^p). If \Sigma_1 \vDash A and \Sigma_2 \vDash A, then \Sigma_1 \cap \Sigma_2 \vDash A ___ holds

sometimes

Which of the following statements about the formula \neg p \land q is not true?

it is a disjunctive clause

The set of connectives \{ \land, \lor, \to \} is ___ for propositional logic

inadequate

The halting problem about Turing machines is undecidable. For any Turing machine T and any input w, it is ___ possible to have an algorithm that decides whether T halts when run on input w

sometimes

The halting problem about Turing machines is undecidable. It is ___ possible to have an algorithm that, for any Turing machine T and any input w, decides whether T halts when run on input w

never

Let A \in \text{Sent}(\mathcal{L}). Then it ___ holds that \emptyset \vdash_{PA} A and \emptyset \vdash_{PA} A and \emptyset \vdash_{PA} \neg A

never

Let A \in \text{Sent}(\mathcal{L}). Then it ___ holds that \emptyset \not \vdash_{PA} A and \emptyset \not \vdash_{PA} \neg A

sometimes

Let A \in \text{Form}(\mathcal{L}^p). If \emptyset \vDash \neg A, then A is

a contradiction