Vector Calculus

vector function

r(t)=<f(t), g(t), h(t)>

space curve

A curve which may pass through any region of three-dimensional space, as contrasted to a plane curve which must lie in a single plane.
I->R^3

r(t)=<cos(t), sin(t), t>
x=cos(t), y=sin(t), z=t

circular cylinder/ helix (spiral), counterclockwise, projection on xy-plane is r(t)=<cos(t), sin(t), 0>, spirals upward since t is positive

how to parametrize

r(t)=(1-t)r0+tr1

x^2+y^2=1

z=0, x=cos(t), y=sin(t)

torus

donut-shaped

unit tangent vector

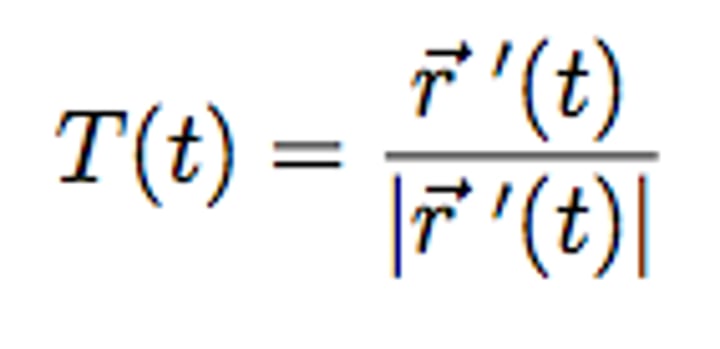
find parametric equations for the tangent line to the helix

page 849, example 3

differentiation rules

page 850

equation for arc length

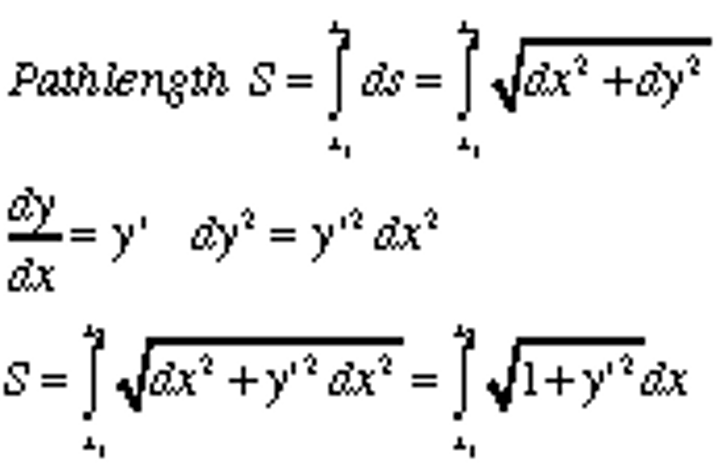
arc length

integral a to b of magnitude of r'(t) dt

smooth curves

no sharp corners or cusps

curvature

k= ||T'||/ ||r'||
T is unit tan vector

parametrization of circle at origin, radius a

r(t)=<acos(t), asin(t)>

curvature

k(t)=||r' x r"||/||r'||^3

unit normal

N(t)=T'(t)/|T'(t)|

binormal vector

B(t)=T(t)xN(t)

gradient of f

<df/dx, df/dy, df/dz>

directional derivative

Du f(x,y,z)= gradient of f dot u
u=unit vector

tan plane

fx(x-x0) + fy(y-y0) + fz(z-z0)=0

ave value

1/(b-a) integral from a to b of f(x) dx

integration by parts

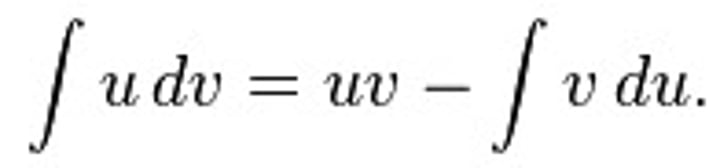
polar coordinates

r^2=x^2+y^2, x=rcos theta, y=rsin theta
dxdy=r dr dtheta

surface area of z=f(x,y)

double integral of sqrt of (fx^2 +fy^2 +1) dA

area of surface of revolution

double integral of sqrt (1 + (dz/dx)^2 + (dz/dy)^2) dA

mass

triple integral of density dV

center of mass

x bar = triple int. x*density dV

moment of inertia

Ix = triple int. (y^2+z^2)*density dV

cylindrical coordinates

x=rcos(t), y=rsin(t), z=z

spherical coordinates (p, theta, phi)

p greater or equal to 0, phi between 0 and pi
x=psin(phi)cos(theta), y=psin(phi)sin(theta), z=p*cos(phi)
p^2=x^2+y^2+z^2

Jacobian

d(x,y,z)/d(u,v,w)
x across, u down

change of variables in a double integral

double int f(x,y,z) dV = triple int f(x(u,v,w), y(u,v,w), z(u,v,w))*|J|dudvdw