Week 2- Factorial ANOVA revision

03/10/24

ANOVA types

• Two-way- 2 independent variables, better than t-tests as they can look at the impact of multiple manipulations on the data and explore the interaction effect

  • ANOVA can tell you whether the influence of one of the variables on scores is modulated by changes in other variables

• Three-way- 3 independent variables

ANOVA- Interaction effects

• Can answer questions where there’s multiple interactions that effect the research answer e.g. driving in fog- day/night conditions and clear/foggy conditions, both effect distance and combined might make a bigger difference than singular

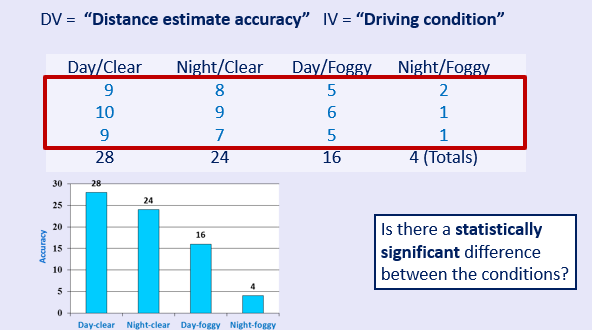
• 4 conditions, 3 participants; IV- time and weather, DV- accuracy of distance estimate

Driving time/weather example- results

• Most accurate in day/clear, least in night/foggy- clear when you make a graph as compared to a table- need statistical support for this!

• Average performance in Day driving (mean = 22) is better than that for Night driving (mean = 14)

• Average performance in Clear driving (mean = 26) is better than that for Foggy driving (mean = 10)

Driving time/weather- statistical support

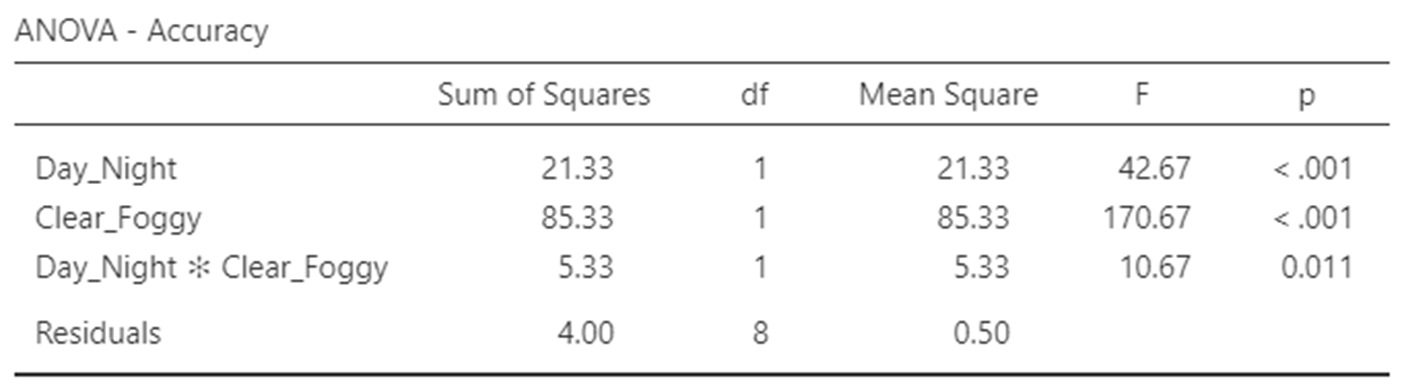
• Driving during day .vs. night has a reliable effect on distance judging performance (p< .001)

• Performance is also dramatically affected by foggy .vs. clear conditions (p< .001)

• The influence on performance in day .vs. night driving conditions changes depending on whether it’s foggy .vs. clear (0.011) F ratio is far smaller, showing it’s not as highly significant

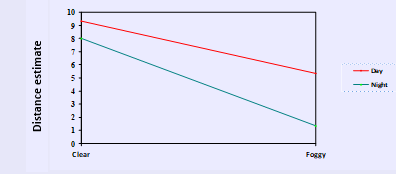
Driving time/weather- effect comparisons

• Explaining the main effects- the bigger the difference between the 2 lines, the more significant the result (look at the midpoint of the main axis of that IV)

• Both lines are on a gradient but they don’t cross over so not as pronounced interaction

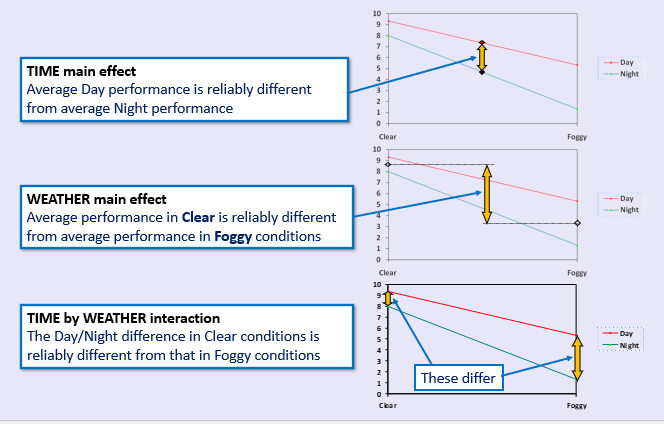
Driving time/weather- describing main effects and interaction

• Distance estimates are affected by whether people are driving during day or at night (the TIME main effect)

• Distance estimates are affected by whether people are driving in foggy or clear conditions (the WEATHER main effect)

• The average difference in Day compared with Night estimates is reliably affected by whether people are driving in foggy or clear conditions (the TIME*WEATHER interaction)

Running a 3 way ANOVA

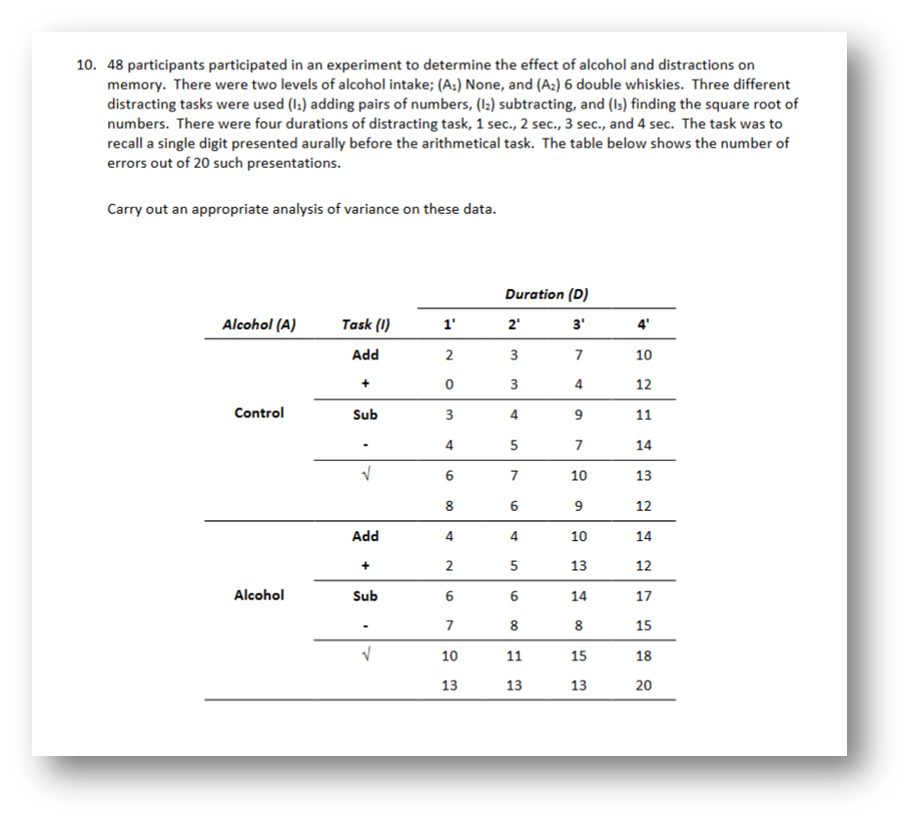
Data should be F- 2dp and P- 3dp

3 way ANOVA example results

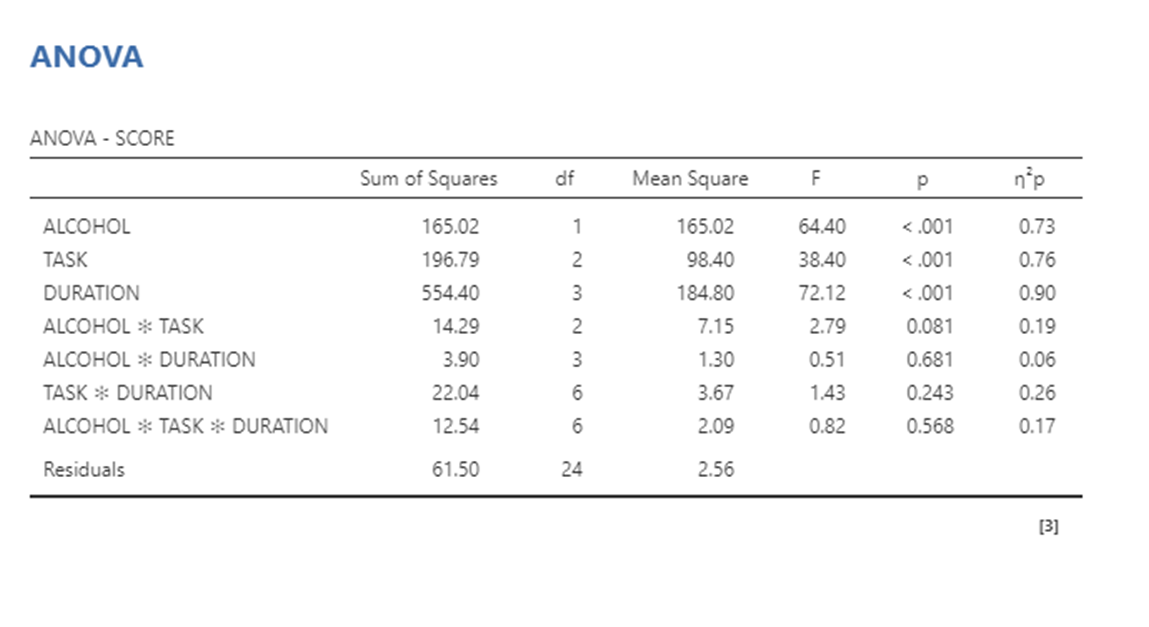
F ratio is signal .vs. noise- real interactions is our signal and noise is other things that are effecting it/error term (possibility that interaction is due to chance)

Planned .vs. unplanned contrasts

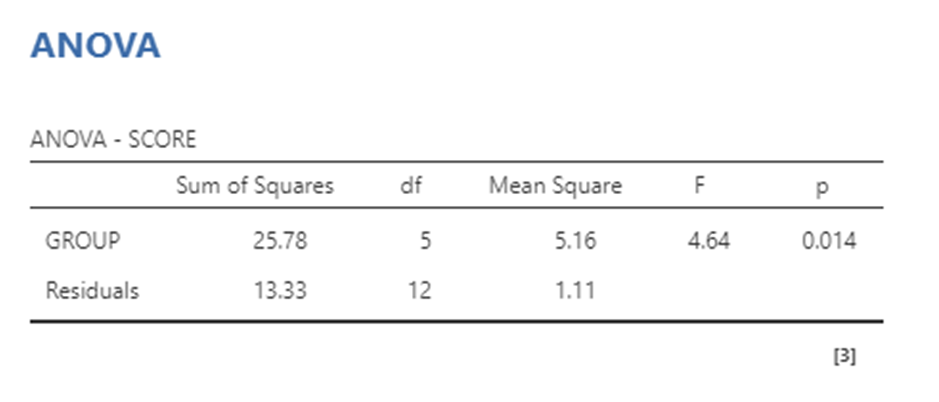
Need to do a contrast to see where the difference is- can be planned (a priori, designed before the experiment) or unplanned (post-hoc, a posteriori, designed after the experiment)

Post-hoc procedures

• Various procedures include the Newman/Keuls test, Duncan’s Multiple Range test, Tukey’s test, Dunnett’s test and the Scheffé test (hardest to pass)

• These tests reduce the likelihood of Type 1 error by increasing the critical value of the test statistic

Post-hoc- running this contrast

• Run the contrast, ignore the C1 P value (only for planned comparisons)

• Scheffe criterion = (k - 1) x Tabled value of F_{k-1, error df}

• K= no .of levels of the factor being examined

• Error df= degrees of freedom in the original ANOVA (same as contrast table)

• In example- k= 6 (as there were 6 groups) and error df= 12

• Look up critical value in F table for 5,12 and times it by 5 (k-1)

• A calculated contrast F-ratio can be declared as significant at the 5% level if the computed value is greater than or equal to the Scheffé criterion