Derivatives

Deliverable Contract

Payment and shares must be exchanged at the settlement date

Cash-Settled Contract

Only gains and losses from the forward contract are exchanged at settlements

Derivative Advantages

• Low-cost exposure and leverage – Derivatives allow investors to gain exposure to a risk at a low cost, enabling highly leveraged investments in the underlying asset.

• Lower transaction costs – Derivatives positions often incur significantly lower transaction costs than equivalent trades in the cash market.

• Reduced market impact – Initiating a derivatives position tends to have less impact on the market price of the underlying asset compared to a similar position in the cash market.

Hard vs Soft Commodities

• Hard

  • Typically mined or extracted

• Soft

  • Typically grown

Exchanged-traded derivatives

Standardized and backed by a central clearinghouse

Central Clearinghouse

Opposite position to each side of a trade - novation

• guarantees and minimizes counterparty credit risk

• requires deposits from both participants when a rade is initiated

Benefits of standardization

1. Increased liquidity – Standardized contracts are easier to trade and attract more market participants.

2. Greater transparency – Prices and terms are publicly available and consistent across trades.

3. Lower trading costs – Uniform terms reduce the complexity and expense of trading.

4. Ease of exit – Positions can be closed by taking the opposite side in the same contract.

5. Simplified clearing and settlement – Standardization supports centralized clearing and reduces operational risk.

Central counterparty/ Swap Execution Facility

• CCP

  • 2008 financial crisis Central Clearing Mandate

  • Takes on counterparty risk of both sides

• Swap Execution facility

  • Information sent to SEF when dealer makes a swap trade

Price Limits

Exchange-imposed limits on how much each day’s settlement price can change from previous day.

• Limit on how high or low settlement price can move

Circuit Breakers

Futures price reaches a limit price, trading derivative is suspended for a short period.

Swaps

Two payments netted so that only one net payment is made

Credit Default Swap CDS

• Protection buyer makes fixed payments on the settlement dates and the protection seller pays only if the underlaying has a credit event

Forward Commitment

Legally binding promise to perform some action in the future.

• Forward, futures, and most swaps

Contingent claim

Claim that depends on a particular event

• Options

  • event of price movement

• CDS

  • event of default

Derivative advantages over cash market transactions

• Change Risk Allocation: Hedge, exposures, swaps

• Synthetic Risk Exposure: Investors can use options to modify existing positions—e.g., buying puts to limit downside risk or calls to gain upside without full exposure.

• Information Discovery: Prices of derivatives (especially options and futures) reveal market expectations, such as implied volatility or future interest rates.

• Operational Advantages:

  • Ease of Short Selling: Derivatives make shorting simpler compared to borrowing physical assets.

  • Lower Transaction Costs: Especially true in commodities, where storage and transport costs are avoided.

  • Leverage: Derivatives require less upfront capital for the same exposure.

  • Liquidity: High liquidity enables large trades with minimal capital.

• Market Efficiency: Derivatives enhance price efficiency by reducing costs of arbitrage and enabling better exploitation of mispricings.

Risks of Derivatives

• Implicit Leverage: Derivatives require less initial capital (e.g., futures margin as low as 3–12%), resulting in high leverage (e.g., 8:1 to 33:1), which amplifies both gains and losses.

• Basis Risk: Occurs when the underlying asset of the derivative does not perfectly match the asset being hedged. Example: Hedging a stock portfolio with an index future that doesn’t perfectly track the portfolio, or timing mismatches in agricultural futures.

• Liquidity Risk: Derivatives may generate margin calls that do not match cash flows from the underlying exposure. Failure to meet margin calls (e.g., by a farmer hedging wheat prices) can lead to the hedge being closed and losses realized.

• Counterparty Credit Risk:

  • Options: Buyer faces credit risk if the seller defaults; seller does not, having already received the premium.

  • Forwards: Both parties face risk unless mitigated with margin, mark-to-market, or clearinghouse arrangements.

  • Futures: Lower risk due to margin requirements, daily mark-to-market, and clearinghouse guarantees.

• Systemic Risk: Excessive speculation and interconnected exposures can lead to financial instability. Regulations (e.g., central clearing for swaps) aim to reduce this risk.

Hedge Accounting: Cash Flow, Fair Value, Net Investment

Hedge Accounting allows firms to recognize gains and losses on qualifying derivative hedges at the same time as the corresponding changes in the value of the hedged assets or liabilities, reducing volatility in financial statements.

Types of Hedges:

1. Cash Flow Hedge:

   • Hedges variability in future cash flows.

   • Example: Hedging future foreign currency receipts with forwards or converting floating-rate debt to fixed with an interest rate swap.

2. Fair Value Hedge:

   • Hedges changes in the fair value of assets or liabilities.

   • Example: Using derivatives to stabilize the value of inventory or fixed-rate debt.

3. Net Investment Hedge:

   • Hedges currency risk in the value of a foreign subsidiary’s equity.

   • Example: Using currency forwards or futures to reduce exchange rate effects on consolidated equity.

Replication

Creating a portfolio with cash market transactions that has the same payoffs as a derivative for all possible future values of the asset

Convenience Yield

Holding rare commodities may have non-monetary benefits

• can drive up prices temporarily

Interest Swaps vs Durations

• Payer

  • Decreases Duration

• Receiver

  • Increases Duration

Short/Long forward

• Short

  • Sell at maturity

  • benefit from depreciating price

• Long

  • Buy at maturity

  • benefit from appreciating price

(Reverse) Cash and Carry Arbitrage

• Cash and Carry Arbitrage F0T > S0*Rf

  • Sell Forward, Borrow, and Buy Share

  • Pay Loan, Receive Forward (give share) → riskless gain

• Reverse Cash and Carry Arbitrage F0T < S0*Rf

  • Buy Forward, Short, Lend

  • Receive Loan, Buy from forward (cover short)

Why can futures prices differ from forward prices due to interest rate correlation?

• Futures settle daily (mark-to-market), forwards settle only at maturity.

• If interest rates and futures prices are positively correlated:

  • Long futures get cash inflows when rates are high → can earn more interest.

  • Pay margin when rates are low → lower opportunity cost.

  • → Futures prices tend to be higher than forward prices.

• If negatively correlated:

  • Futures cash flows and interest rates work against each other → futures prices tend to be lower.

• If uncorrelated or constant rates, futures and forward prices are roughly equal.

Why is the FRA payoff asymmetric when interest rates move equally above or below the forward rate?

Because the payoff is the present value of future interest savings/losses, discounted at the realized MRR.

• Higher MRR → heavier discounting → smaller gain

• Lower MRR → lighter discounting → larger loss
  So, a +1% move gives a smaller gain than the larger loss from a −1% move.

Convexity Bias

Convexity bias means forward values rise more from rate decreases than they fall from rate increases.
This asymmetry grows with time and causes futures ≠ forward prices, especially for long-term rates.

What causes pricing differences between futures and forwards, especially for interest rate contracts?

• Futures: Settled daily (mark-to-market); gains/losses realized immediately.

• Forwards: Settled once at maturity; no interim cash flows.

• If interest rates and futures prices are positively correlated, futures are more valuable than forwards due to reinvestment benefits when rates are high (convexity bias).

• Forwards exhibit asymmetric valuation (convexity):
  Value rises more when rates fall than it falls when rates rise.

• In practice, the pricing difference is small due to short maturities and low funding costs.

Par Swap Rate

Swap fixed rate that gives the swap a zero value a initiation

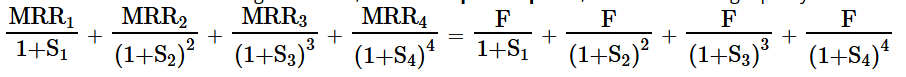
Swap vs. Series of Forward Contracts (FRAs)

• A swap is a series of cash flows exchanging fixed vs. floating rates.

• A 1-year quarterly interest-rate swap = one known payment + 3 equivalent FRAs.

• MRRn – F = payment to fixed-rate payer at time n.

• Swaps can be replicated by FRAs (forward contracts on interest rates).

• Key difference: FRAs are individually zero-value at initiation; swaps use one fixed rate (par swap rate), so individual embedded FRAs may have positive/negative value, but total = 0.

Swap Price vs. Swap Value

• Swap Price = Fixed rate set in contract (par swap rate).

• Swap Value = PV(expected floating payments) – PV(fixed payments).

• At initiation: value = 0 (by setting fixed rate = par swap rate).

• After initiation: value changes with interest rate expectations.

• Fixed-rate payer benefits if future floating rates ↑.

• Floating-rate payer benefits if future floating rates ↓.

Moneyness

Whether an option is in the money or out of the money

Exercise/Intrinsic Value

Immediate profit from exercising the option

Maximum of zero and the amount that the option is in the money

Time Value

Extra value from future potential

amount by which the option premium exceeds the exercise value

Upper Bound for Calls and Puts

• Calls

  • c_t ≤ S_t

  • Cost cannot be more than the price itself

• Puts

  • p_t≤X(1+Rf)^-(T-t)

  • PV of the exercise price discounted at Rf

Lower Bound and Upper Bounds for Options

Factors affecting option values

• Underlying Price (S):

  • 📈 Call ↑, Put ↓

• Exercise Price (X):

  • 📈 Call ↓, Put ↑

• Risk-Free Rate (r):

  • 📈 Call ↑, Put ↓

• Volatility (σ):

  • 📈 Call ↑, Put ↑

• Time to Expiration (T):

  • 📈 Usually increases both (but very deep in-the-money European puts may decrease)

• Dividends / Carrying Costs:

  • 📉 Call ↓, Put ↑

  • 📈 Storage costs → Call ↑, Put ↓

Put Call Parity

• Fiduciary Call

  • Call + Riskless bond

    • Out of money payoff

      • X

    • In money

      • X + (S - X) = S

• Protective Put

  • Share + Put

    • Out of money payoff

      • S

    • In money payoff

      • (X - S) + S = X

Firm Value comparison with Call/Put

• Equity

  • Long call on firm’s assets

    • S - X or zero

    • V - D or zero

• Debt

  • Long bond + Short put

    • X - S or zero

    • D - V or D

Future vs Forwards Payoffs

Topic	Futures (e.g., STIR)	Forwards (e.g., FRA)
Payoff Type	🔹 Linear	🔸 Convex
Settlement	Daily mark-to-market (MTM)	Single payment at contract fixing date
P&L Realization	Daily gains/losses posted to margin account	Settled once at start of interest period
Reinvestment	Yes — you can reinvest daily gains	No — single net payment, no reinvestment
Sensitivity to Volatility	Less — linear change with rate moves	More — value depends on rate path & timing
Convexity Adjustment	❌ Not needed	✅ Needed to match futures value
Use Case	Transparent hedging/trading of rate moves	Locked-in rate agreements over a future period