RSF (regime sinusoïdal force)

Le concept

Amplitude plus élevé de s(t) pour un e(t)

Tension d'entrée

e(t)=Um cos(ωt)

intensité

i(t)=Im cos(ωt - φ)

φ= déphasage en rad

Déphasage

φ=2π×(Δt/T)

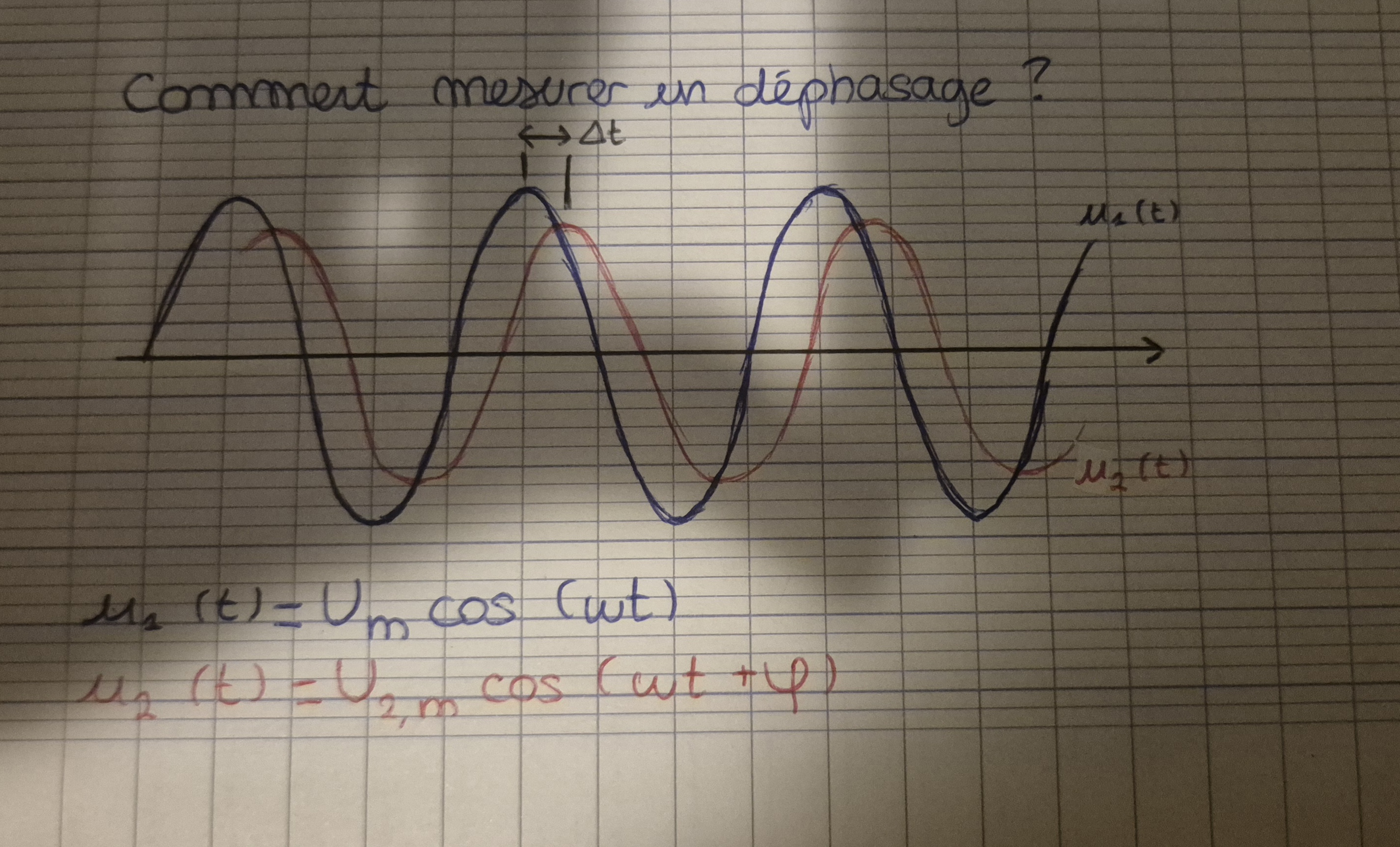
Cas particulier phase

φ=π :opposition de phase

φ=π/2 : quadration de phase (Δt = T/4)

Solution particulière

-négligeable

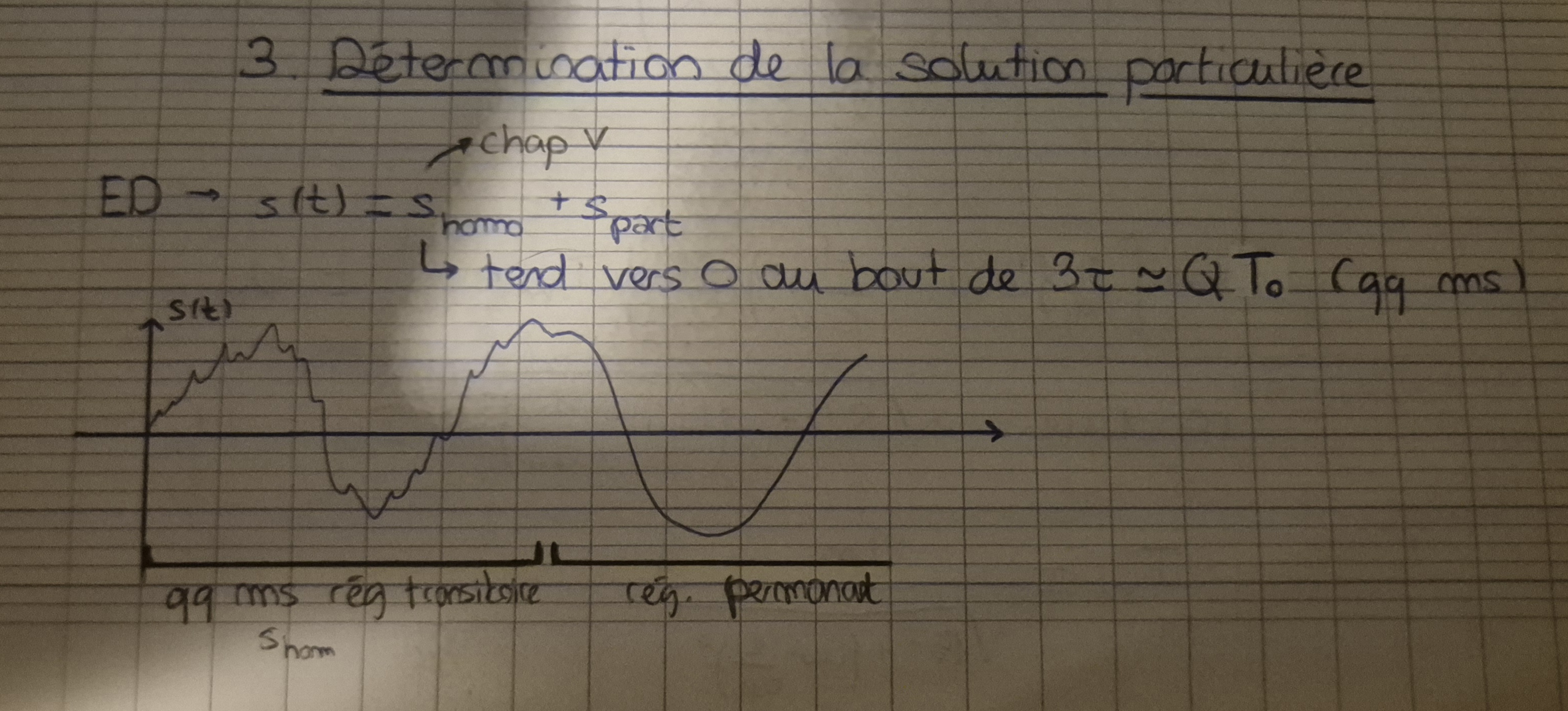
Methode complexe

-souligner les grandeur complexes

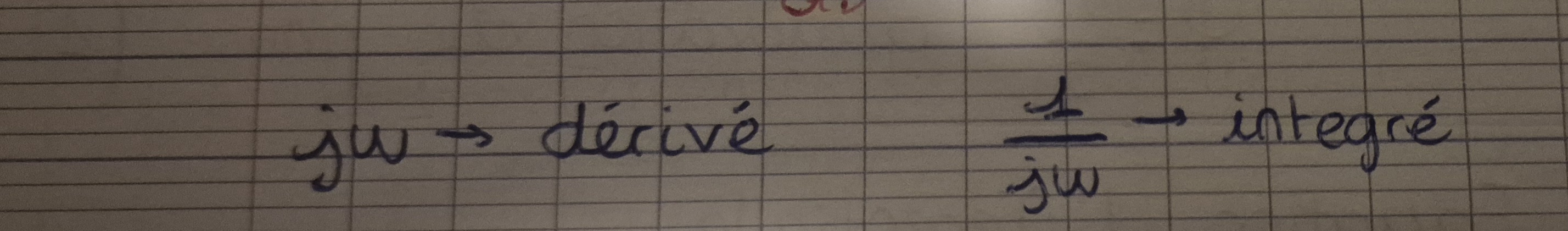
Déterminer l'amplitude et l’amplitude max

-module pour trouver l'amplitude

(f=ω/2π)

Déterminer φ

Argument

φ=arctan(Im/Re)

Impédance

Zc=1/Jcω

ZL=jLω

Zr=R

Opérations avec impédance

-addition en série Zeq= ΣZi

-addition en dérivation 1/Zeq =Σ1/Zi

-Pont diviseur de tension

-|Z|=Ω

⚠ les amplitudes ne s'additionnent pas

Admittance

Y=1/z (complexe)

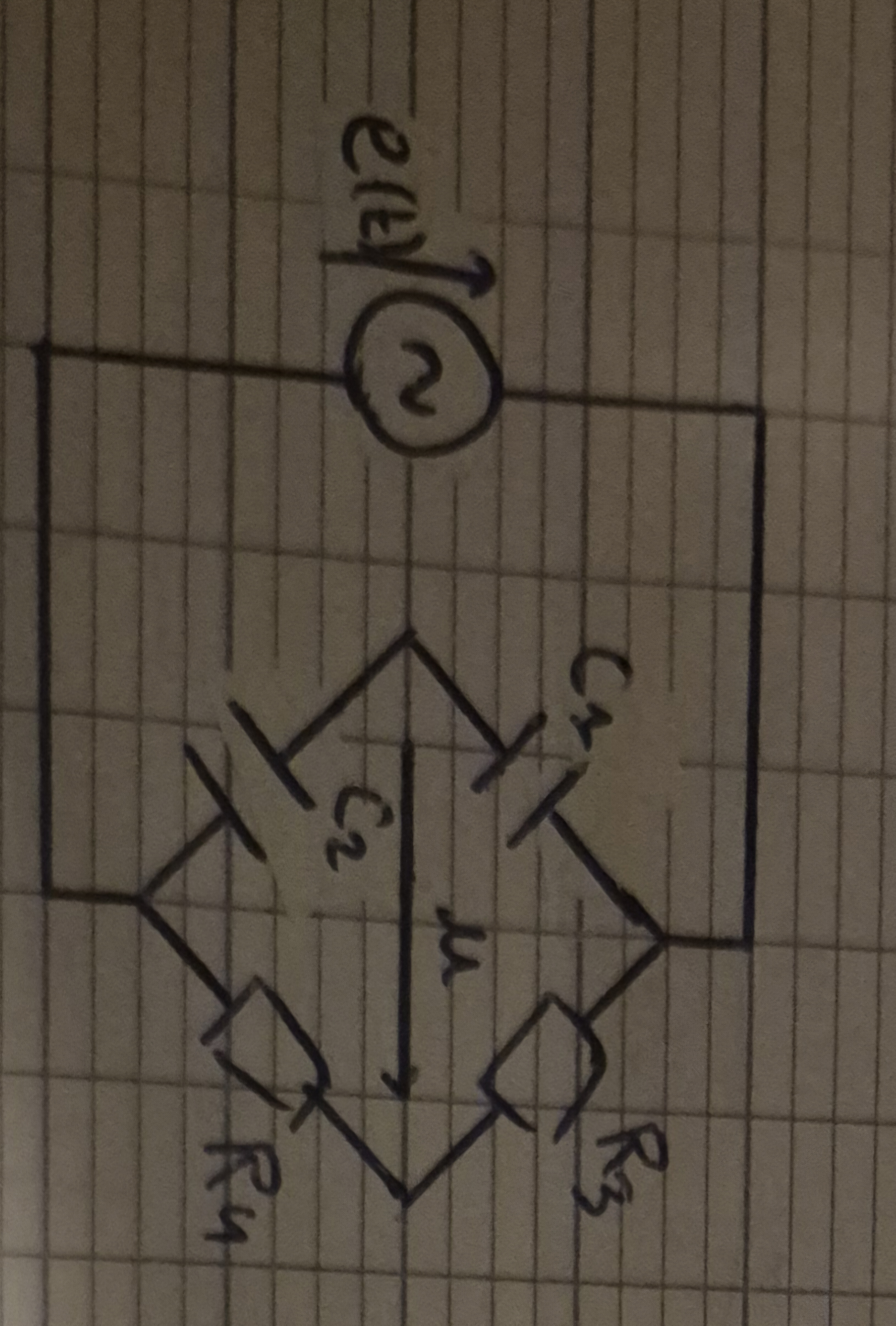
Pont de Wheatstone

u=u1+u3

u=R1/(R1+R2) E -R3/(R3 +R4) E

Pont à l'équilibre si u=0

Formule en croix

R1R4=R2R3

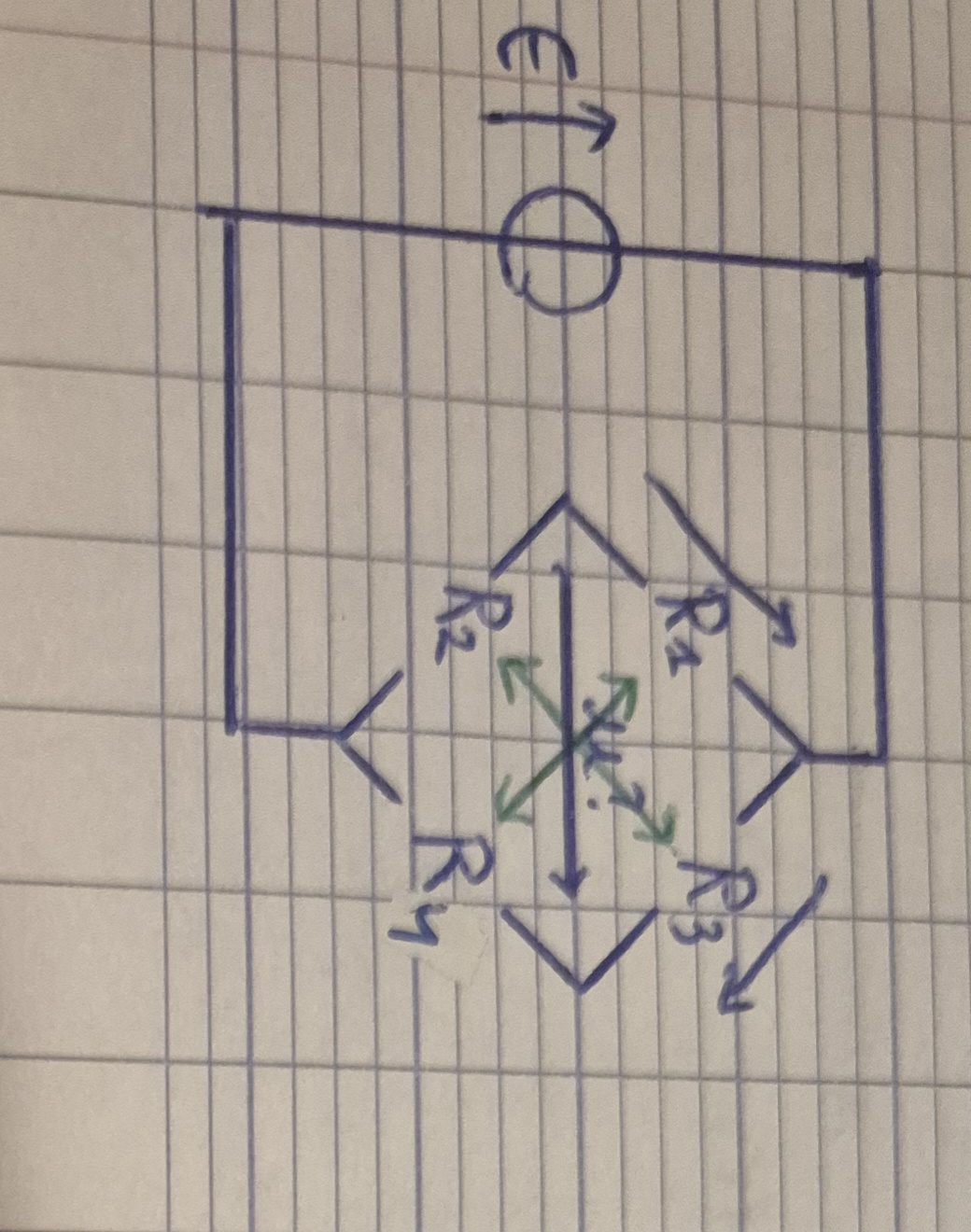
Pont de Sauty

Methode en croix

Amplitude complexe

Im(complexe) =Im e(-jφ)

Umesure voltmètre

Ueff=Um/sqrt(2) en sinusoïdal pur

Ueff=sqrt(<u²>) sinon

Résonance d'intensité

Il existe un fréquence de resonce pour laquelle Um est maximum

Im=Um/|zeq|

Bande passante à -3db (Im/sqrt(2))

Im(ω1)=Im(ω2)=Um/Rsqrt(2)

-résolution de Um/|Z| = Um/Rsqrt(2)

Resolution Δ

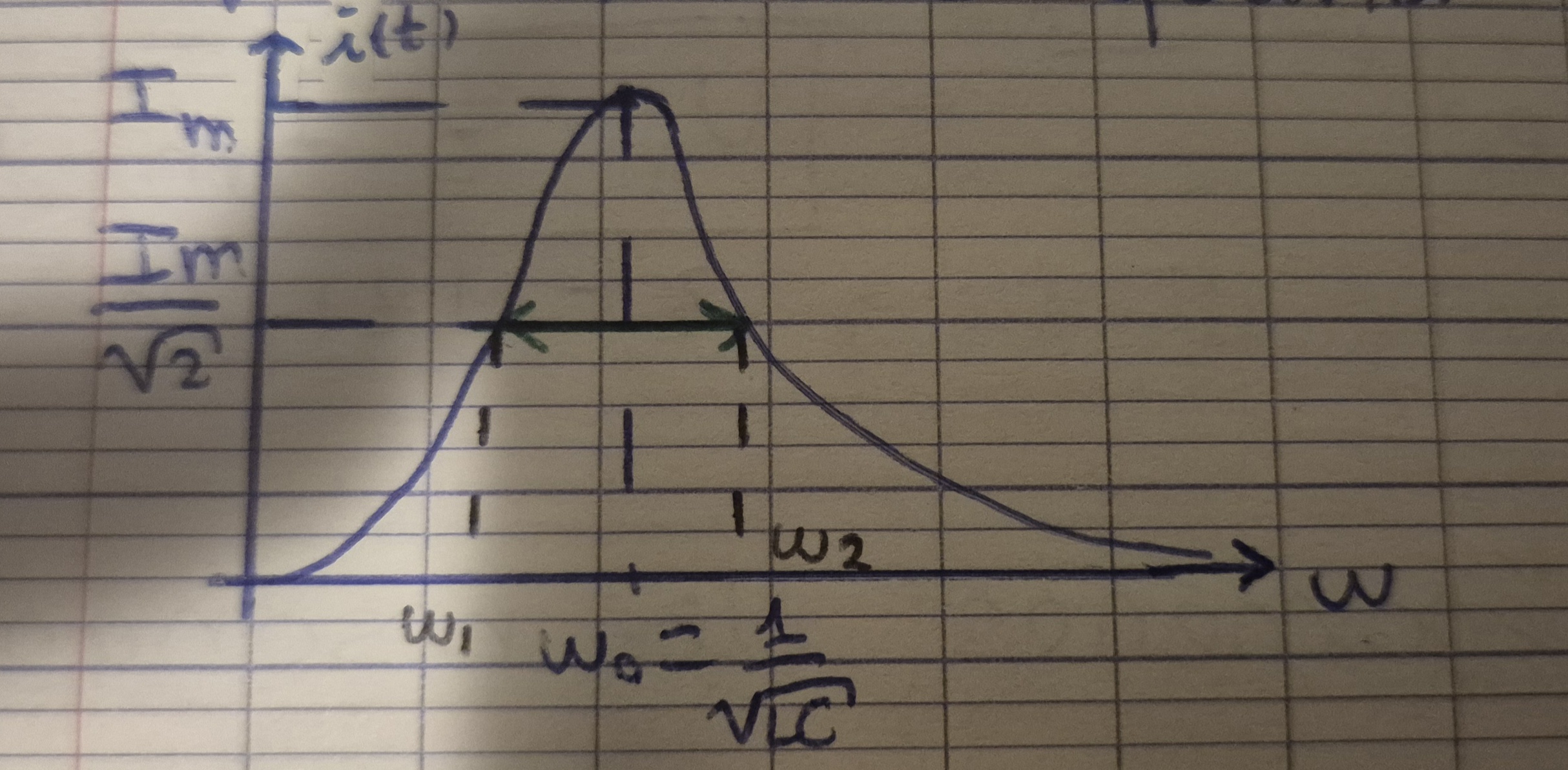
Bande passante

BP =ω2 - ω1=L/R

Bande passante relative

Δω/ως =R/Lω0 =1/Q

Vocabulaire

Q=facteur de sélectivité

Résonance avec grande acuité

Résonance en tension

Pont diviseur de tension

-on pose ωo=1/sqrt(LC)

-pulsation réduite x=ω/ωο

-module

-on pose g(x) = ce qui est sous sqrt

-dérivation

-extremum (g’(x)=0)

Q>1/sqrt(2) =0.7

Donc résonance pas systématique

Résonance en elongation

Complexe → module