CRIT 111-005 Foundations Logical Reasoning S25 (BSU) module 2 test sudy guide

~ (tilde)

negation

(Isn't, Wouldn't, Won't, Not, Can't, Couldn't, Doesn't)

e.g:

Cats are not adorable

. (dot)

conjunction

(And, Also, Moreover, Whereas, But, Furthermore)

e.g:

Fred is both nice and an idiot

∨ (wedge)

disjunction

(Either/or, Or, Unless)

e.g:

Fred is either nice or an idiot

⊃ (horseshoe)

conditional

(If....then___, If, When, Only if)

e.g:

If Fred is nice, he's an idiot

≡ (triple bar)

biconditional

(If and only if, When and only when, Just in case)

e.g:

Fred is nice if, and only if, he's an idiot

Modus Ponens

if P then Q, and P; therefore, Q

(the premise affirms the antecedent)

Affirming the consequent

If P then Q, and Q; therefore, P

(the second premise is the affirmation of the consequent of the original conditional)

Denying the antecedent

if P then Q, but not P; therefore, not Q (the second premise is the denial of the antecedent of the original conditional)

Modus Tollens

if P then Q, but not Q; therefore, not P (the second premise denies the consequent of the conditional in the first premise)

disjunctive syllogism

if the disjunction is true and yet one disjunct is false, then it must be the case that the other disjunct is true

affirming a disjunct

If the disjunction is true and one disjunct is true then it may or may not be the case that the other disjunct is false

lowercase p, q, and r

used to represent statement variables

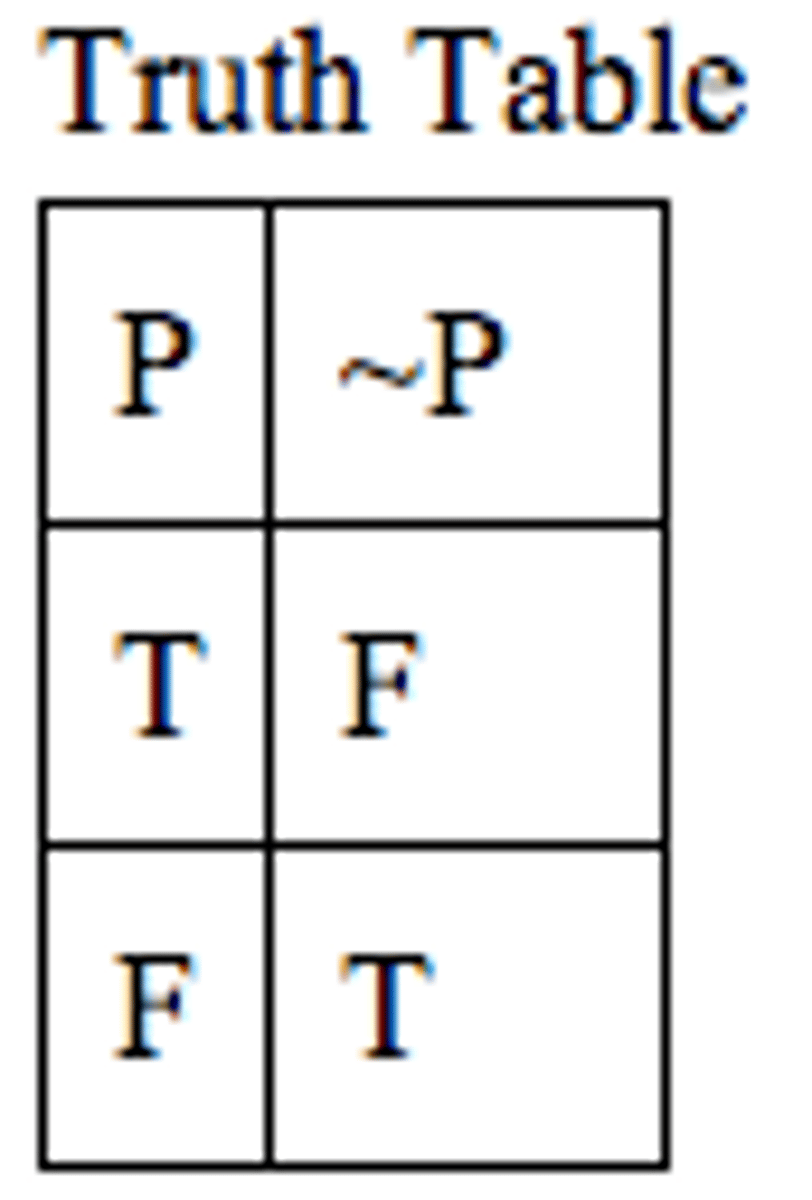
Negation

the opposite of the original statement

(whatever the truth value of p is, ~p will always be its negation)

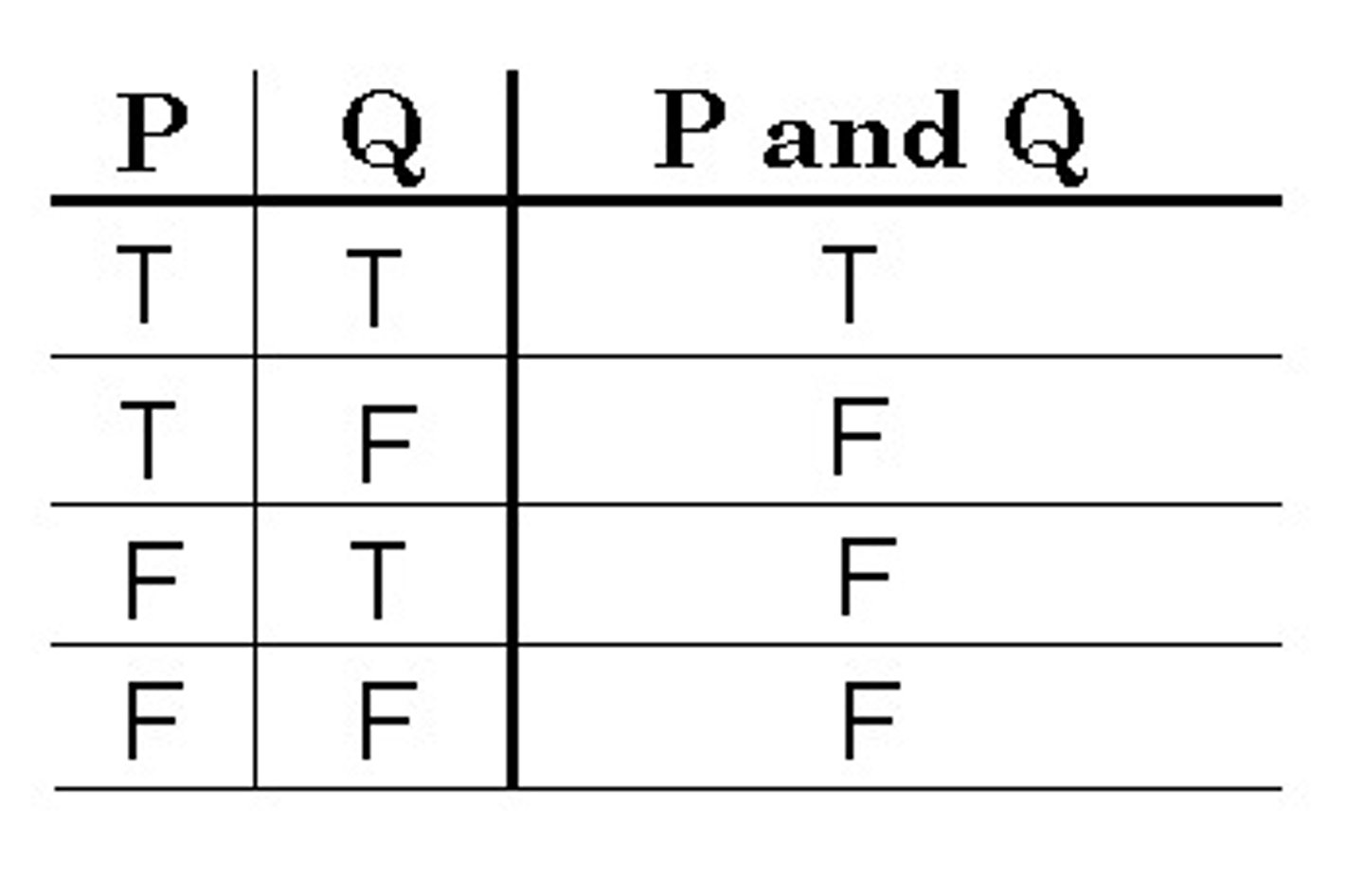
Conjunction

applies to exactly two statements (P . Q)

is true if both of its conjuncts are true

is false if either one, or both, of its conjuncts are false

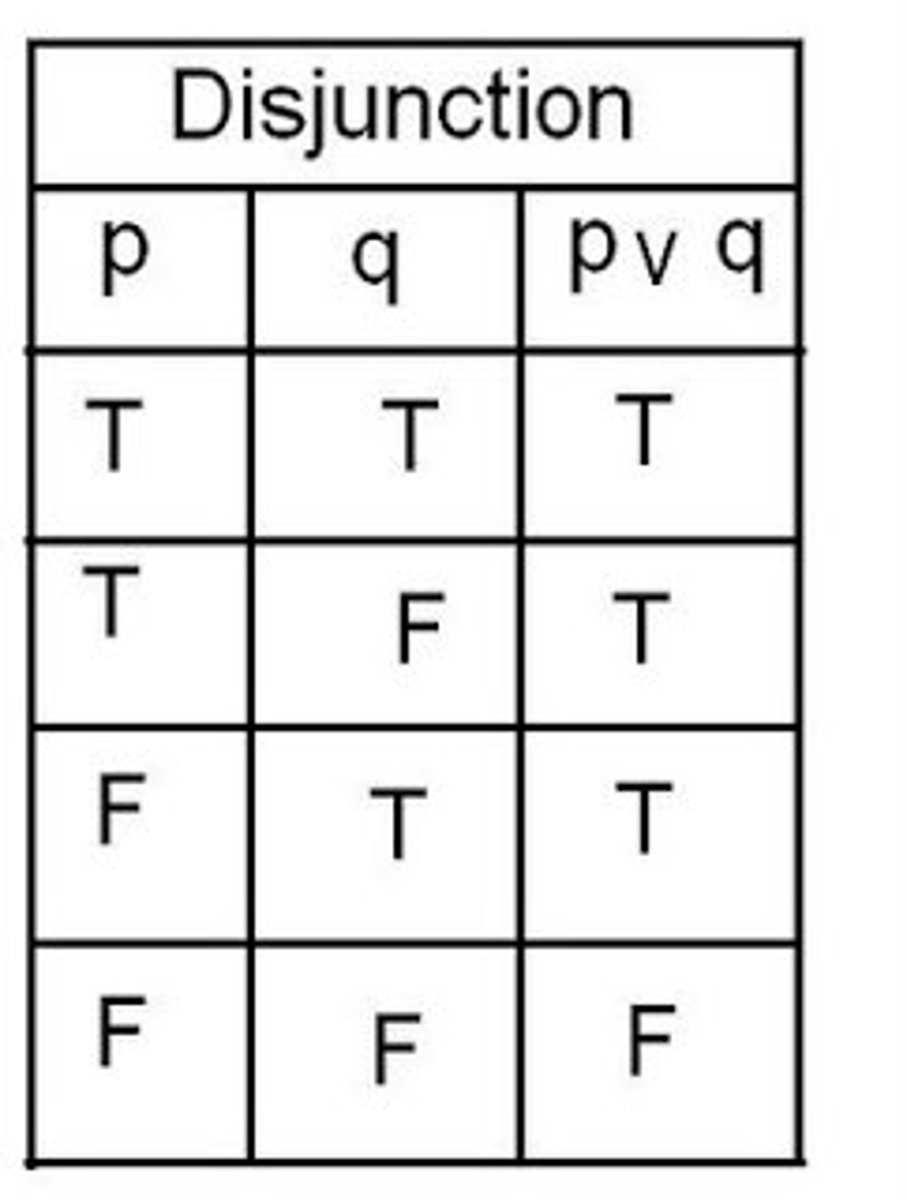
Disjunction

allows for the possibility that both p and q are true (the word "or" can be ambiguous)

Bi-conditional

are only true if both component statements have the same truth values

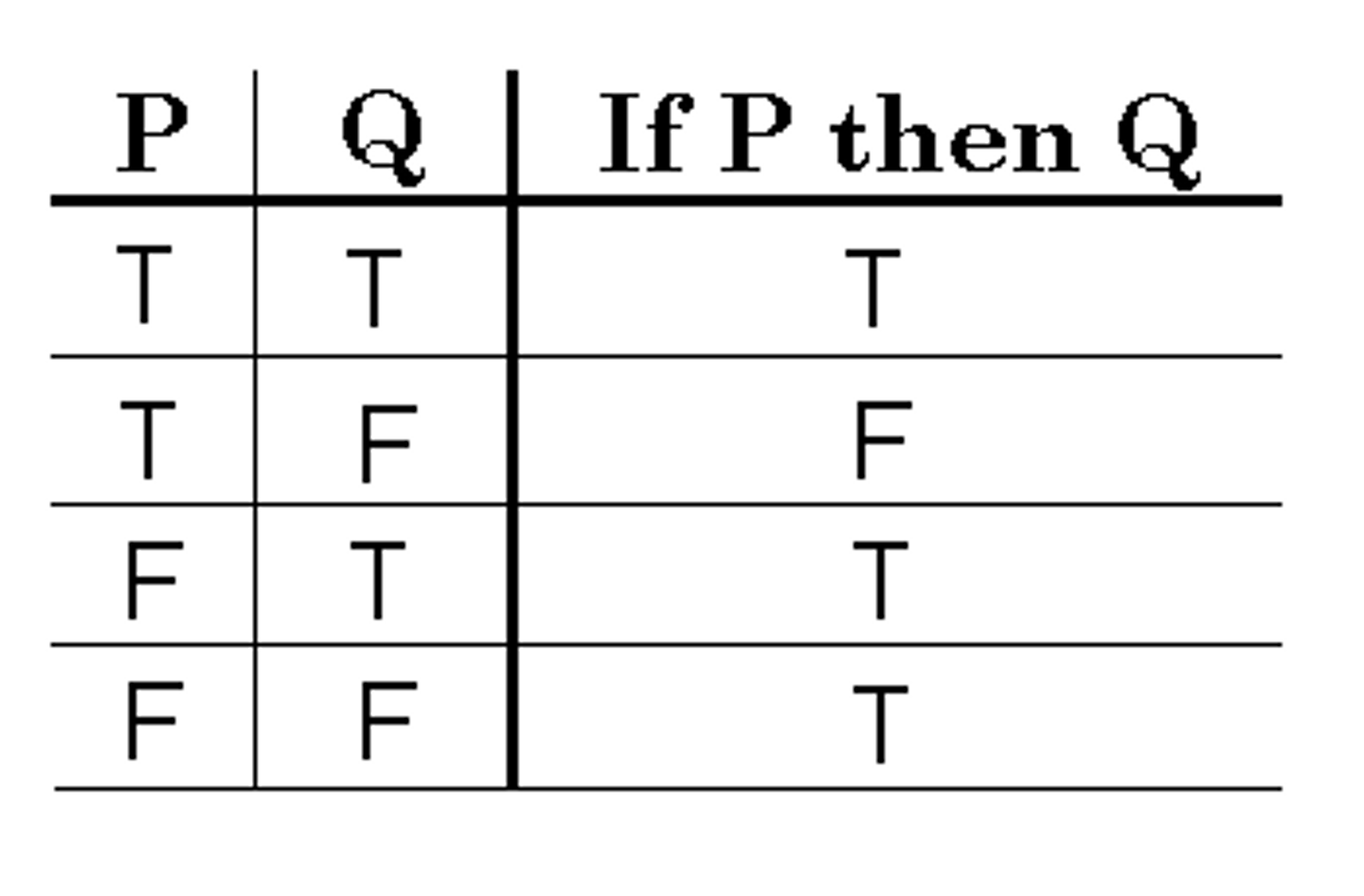
Conditionals

if statements

(the fact p is false, or that p and q are false, does not necessarily make the conditional false)

Sentential Logic

complex/compound statements that are built from simple statements that are either true or false

capital letters

represent simple statements

simple statements

does not have any other statement as a component

e.g:

(Cats are adorable)

compound statement

contains one or more other statements as component parts by combining simple statements with connector words

e.g:

(Although he's nice, Fred is an idiot)

Antecedents

follow the left of the horseshoe (the "if" clause)

consequent

follows the right of the horseshoe (the "if" clause)

sentential logic rule 1

the dot, wedge, horseshoe, and triple-bar are always placed between exactly two statements

e.g:

✅ S ∨ T

❌ P ⊃ R T

sentential logic rule 2

the tilde goes directly in front of the statement it negates

e.g:

✅ ~ S

❌ Q ~

sentential logic rule 3

The tilde cannot be placed by itself between two statements.

e.g:

✅ ~ B

❌ L ~ K

sentential logic rule 4

Parentheses - "(" and ")" - must be used to eliminate any ambiguity in compound statements

e.g:

✅ (P . Q) ∨ R

❌ P . Q ∨ R

main operator

what a well-formed formulae have; a single logical operation whose components are the entire compound statement (avoid the temptation of finding it from left to right)

e.g:

(P ≡ ~Q) ⊃ (S ∨ T)

⊃ is the main operator