Algebra II - 2nd Semester Exam Study Guide

Matching Formulas and Properties - 35 points

Adding Functions

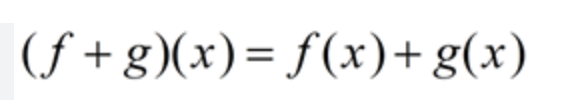
Change of Base

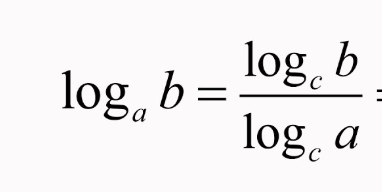
Common Logarithm

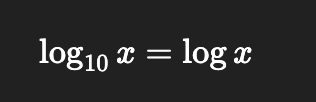
Compound Continuously

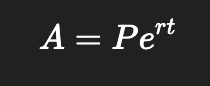
Conjugates

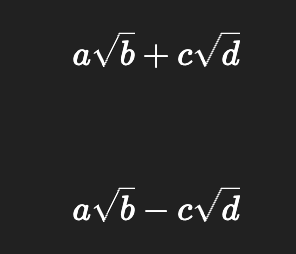
Dividing Functions

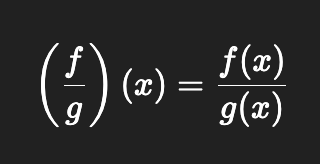
e

aprox. 2.718

Exponential Decay

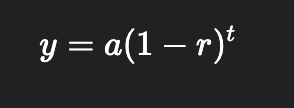
Exponential Function

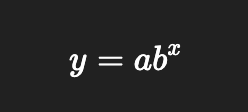
Exponential Growth

Arithmetic Sequences

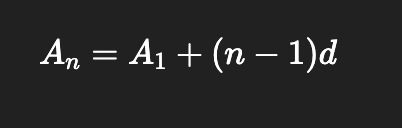
Geometric Sequences

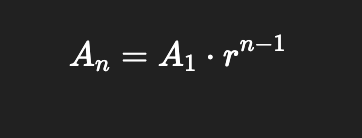
Sum of a finite arithmetic sequences

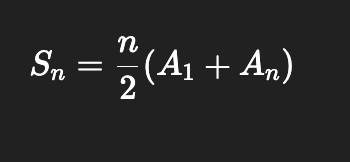
Sum of a finite geometric sequences

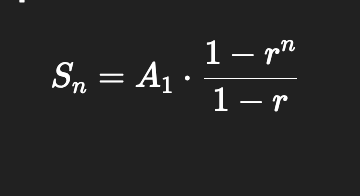
Multiplying Functions

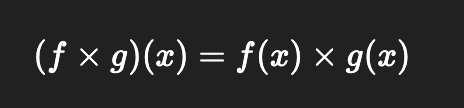
Natural base exponential function

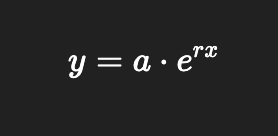
Natural Logarithm

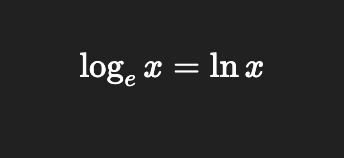
Negative Exponent

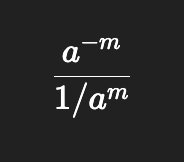
Power of a power

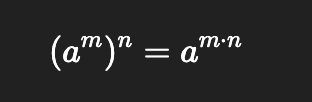
Power of a product

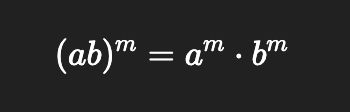
Power of a quotient

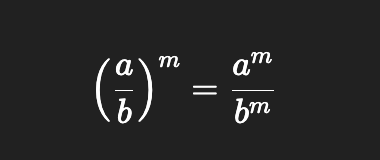
Power property

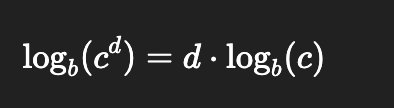
Product of powers

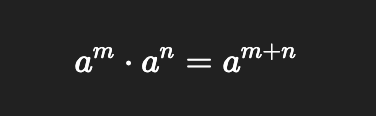
Product Property

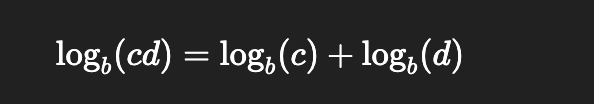
Product Property of radicals

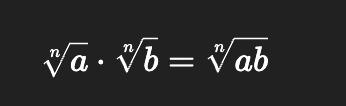
Quotient of powers

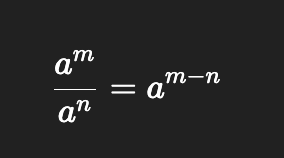
Quotient property

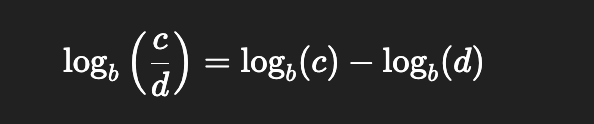
Quotient property of radicals

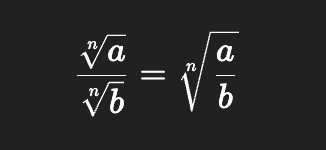
Radical function

√x

Rational Function

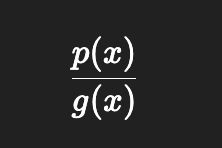
Substracting functions

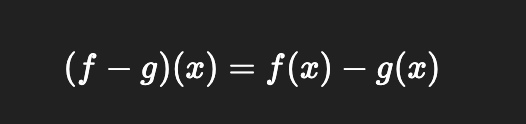
Arithmetic sequence

- a list of ordered numbers where to difference between one term to the next is constant

Compound interest

- interest that is based on an initial amount once accumulated interest

Common difference

- represents the constant different between one term to the next

Common ratio

- represents the common multiplier between any term to the next

Explicit rule

shows how An acts as a function to solve for terms at any position

Exponential equations

- have a variable in the exponent

Extraneous solutions

- Extra solutions that dont work

Finite sequence

- a list with a limited number of ordered numbers

Finite series

- limited number of terms added together

Geometric sequence

- a list of ordered numbers where the ratio of any term to the next term is constant

Horizontal line test

- if you put the horizontal line through a function and it passes through only once then the inverse is a function

Infinite sequence

- a list with an unlimited number of ordered numbers

Infinite series

unlimited number of terms added together

Inverse functions

- reflect over the line y = x

Logarithms

- the opposite of exponential function

Partial sum

the sum of the first n terms that are given in an infinite series

Recursive rule

- shows how An is related to the revious terms given the beginning term

Term

the position of a number in a sequence

Radical function

domain and range : f(x) = √x
x>=0
y>=0

Cube root function

domain and range f(x)=3√x
all real numbers

Rational function

f(x) = 1/x