Microeconomics- Cost revenue & profit maximization

What is a Cost Function?

A cost function c(x) gives the minimum cost of producing output x using labour (cost w) and capital (cost Pk, based on the firm choosing inputs to minimize total cost.

Different cost variables

Fixed costs:

• Costs that must be paid even when the firm produces nothing. Typical examples include cost of capital equipment or long-term leases, which cannot easily be reduced in the short run

Variable costs:

• Costs that change with the level of output(x). Examples include wages of production worker, raw materials and energy used in the production process, and the wear and tear on machinery from actual use.

Marginal cost formula

The change in total cost, when we produce one more unit ot output.

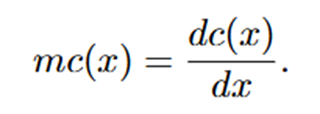
Geometrically: marginal cost corresponds to the slope of the total cost curve at a given level of output

Average cost explantion and formula

AC is the total cost per unit of output. Geometrically, it is a slope from the origin to a point on the cost curve

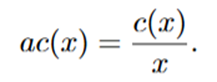
Average variable cost (AVC)

Variable cost per unit of output

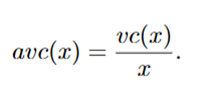
Geometrically is it the slop of a line drawn from the fixed cost intercept of the total cost curve to the point on the curve corresponding to output

Formula for Revenue

Formula: r(x)=p(x)⋅x

·       R(x) = total revenue

·       P(x) = price per unit (depends on how much is sold)

·       X= quantity sold

Inverse demand function

Function p(x)

The function p(x) is called the inverse demand function. It tells us “If the firm wants to sell x unit, what price must it charge?”. In other word, the price depends on the quantity, because demand is downward sloping.

Why is the inverse demand function important

·       A monopolist can’t just decide both the price and the quantity independently. If it sets a high price, it will sell fewer units. If it wants to sell more unit, it must lower price

·       A monopolist = a single firm that is the only seller of a product in the marked.

Average revenue formula and explantion

AR is the total revenue per unit of output.

Formula: ar (x) = r(x) / x

• R(x) = total revenue = p(x) * x’

• Divided by x → gives revenue per unit

So:

• ar (x) = p(x) * x / x = p(x)

This means average revenue = price. This is always true; the money the firm gets per unit is just the price it charges. This rule is not only for monopolists, it is true for any marked structure

Marginal revenue

Extra revenue a firm earns from selling one more unit of output.

Formula: mr (x) = dr(x) / dx

Geometric meaning: MR is the slope of the total revenue curve at a given point

Profitt maximization

Profit is the difference between a firm’s revenue from sales of its output, r(x) and the cost of producing output c(x)

Formula: π(x)=r(x)−c(x) =p(x)x - c(x)

Meaning: the firms earn money from selling unit: p(x) * x but is also spends money to produce them c(x). Profit is simply the difference between these two’

Profitt-maximizing condition

1) Set the derivate equal to 0

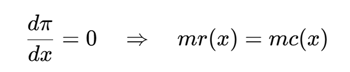
Marginal Revenue (MR) = dp/dx * x +p

Marginal Cost (MC) = c’(x)

RULE

• The firm maximizes profit by choosing the output level where MR = MC

IntutiiTon behind: MR>MC, MR<MC and MR=MC

• If MR > MC → selling one more unit adds more to revenue than it costs → increase output.

• If MR < MC → selling one more unit cost more than it earns → reduce output.

• At MR = MC → the firm is at the sweet spot: maximum profit

Markup

The percentage by which the price a firm charge is above its marginal cost.

Formula for mark-up ratio:

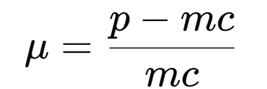
o   If p = mc you get μ=0, then markup = perfect competition (no single firm has market power)

o   If p > mc, then markup > 0 → firm has market power

In words: markup measures how much a firm can “markup “its price over the actual cost of producing one more unit.

Marginal revenue with elasticity

We rewrite MR in terms of elasticity of demand. Formula:

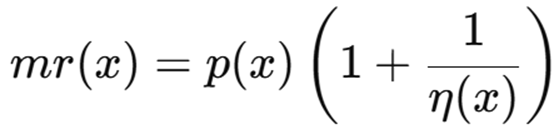
Marginal revenue (MR):  Price – p(x) and  Elasticity of demand η(x)

Why?

• We use the elasticity version of marginal revenue only for monopolies, because elasticity shows how much revenue changes when the firm must lower price to sell more.

Elasticty definition

Formula: η(x)= (dp / dx​) * (x/ p)​.

• It measures how sensitive demand (x) is to price (p), since demand slopes downward, elasiticty is negative. However to aviod confusion, economist usally use = the absolute value

Which gives us the formula:

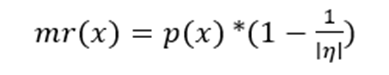
What does this mean for MR

• If demand is elastic (∣η∣>1): MR>0(positve). Selling more increases total revenue

• If demand is unit elastic (∣η∣=1): MR=0, total revenue is maximized

• If demand is inelastic(∣η∣<1):  MR<0(negative). Seeling more reducewrs total revenue

A monopolist will only operate where demand is elastic. If it produced in the inelastic part, MR would be negative → profit would fall

How does elasticity determine a monopolist markup and maket power

A monopolist sets MR = MC, and this leads to a markup that ONLY depens on elasiticty.

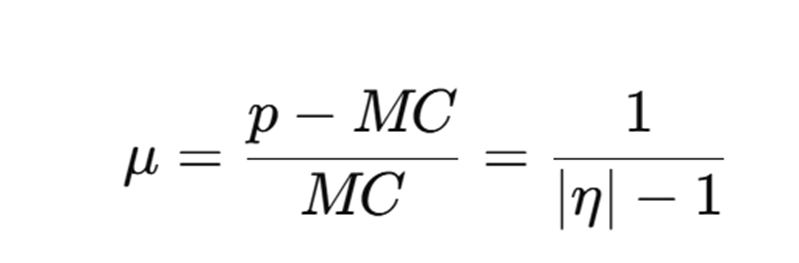
From the formula, we understand elasticity controls the markup and determines market power

Controls the markup

• If demand is elastic (∣η∣ large) → markup is small
  → firm cannot raise price much, they have weak market power

• If demand is inelastic (∣η∣ close to 1) → markup is huge
  → firm can raise price a lot. Strong market power,charge far above marginal cost. Firms what this

Determines market power

• Market power = ability to set price > MC.

  • If inelastic demand → strong market power (big markup).

  • If elastic demand → weak market power (small markup).

  • If p = MC → no market power (perfect competition).

Can a monopolist produce where demand is inelastic, basically will a monopolist ever choose |η| < 1

If |η| < 1, demand is inelastic and the MR formula gives a negative number.
When MR < 0, selling more reduces total revenue.
This happens because consumers do not respond much to price changes, so lowering the price to sell extra units reduces revenue on all units more than the extra units add.

Both total revenue and total cost fall, so profit rises when the monopolist raises the price and reduces output.
Therefore, it is impossible for a monopolist to operate where |η| < 1, because MR is negative and the profit-maximizing condition MR = MC cannot be satisfied.

NB! This differs from “Less elastic” (closer to 1 but still ) → higher markup (firm charges far above cost). “Inelastic” ( ) → impossible, because MR is negative.

Monopolist wants consumers to be and otuput to be

A monopolist wants consumers to be inelastic (for high markup- bascially so that they can raise price above cost) but must choose an elastic output level (because MR must be positive).

What happens when ∣η∣=∞

This is perfect competition

• Firms have no market power.

• They cannot charge above marginal cost.

  • They simply sell as much as they want at the market price.

|η| = ∞ means perfectly elastic demand, zero markup, price equals marginal cost, and the firm behaves as a price taker in perfect competition.

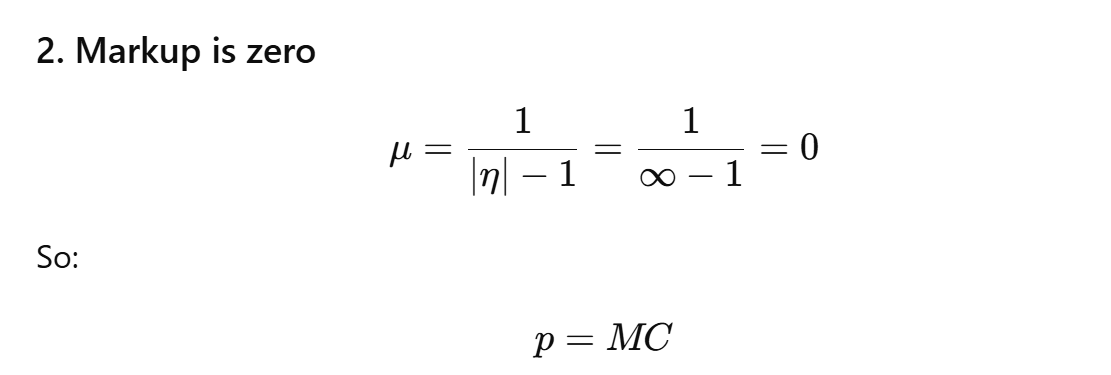
Difference between revenue formula and profitt formula

Revenue is price × quantity, while profit is revenue − total cost.