The inverse of a Matrix 2.2

The identity of a set/operation

The identity of a set/operation is the element of the set that when applied to any other element, leaves the other element unchanged

• the identity under multiplication is 1

• The identity under addition is 0

• The identity under vector addition is the zero vector

The inverse of an element x

The inverse of the element x, in a set is the element that when applied to x, gives the identity

Example: the inverse of 5 under addition is -5

Ex: the inverse of 7 under multiplication is 1/7

Invertibility

Let A be an nxn matrix. A is invertible if there is an nxn matrix C such that:

• CA = I

• AC = I

  where I is the nxn identity matrix

Singular matrix

A singular matrix is a matrix that is NOT invertible

Nonsingular matrix

A nonsingular matrix is an invertible matrix

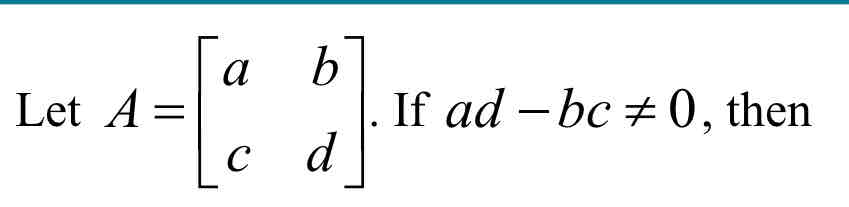
Determining if Inverse (A^-1) of a 2×2 matrix exist

ad - bc is called the determinant of A

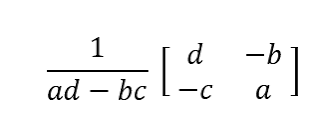
If A is an invertible nxn matrix

The equation Ax = b has the unique solution for every b in R^n

This can be done by applying A^-1 on both of the left sides of the equation

Ax = b

x = A^-1 b

Theorem about invertible matrices

If A is an invertible matrix, then A^-1 is invertible and

• (A^-1) ^-1 = A

If A and B are nxn invertible matrices, then so is AB, and the inverse of AB is the product of the inverses of A and B in reverse order

• (AB)^-1 = B^-1 • A^-1

If A is an invertible matrix, then so is A^T, and the inverse of A^T is the transpose of A^-1

• (A^T)^-1 = (A^-1)^T

An elementary matrix

An elementary matrix is a matrix that is obtained by performing a single row operation on the identity matrix

An nxn matrix A is invertible if and only if…

A is row equivalent to In, and in this case, any sequence of elementary row operations that reduces A to In also transforms In into A^-1

Algorithm for finding A^-1

To find the inverse of A using row-reduction: