math vector/parametric test

vector

a representation of quantities that have both a size (or magnitude) and a direction (such as velocity, acceleration, force and displacement)

equivalent vectors

vectors that have the same magnitude and direction

unit vector

a vector whose magnitude is 1

sketch of a vector

• the initial point is the tail/foot

• the terminal point is the head and MUST have an arrow length to show direction

• the length of the vector is called the magnitude, symbol ||v|| with an arrow over the v

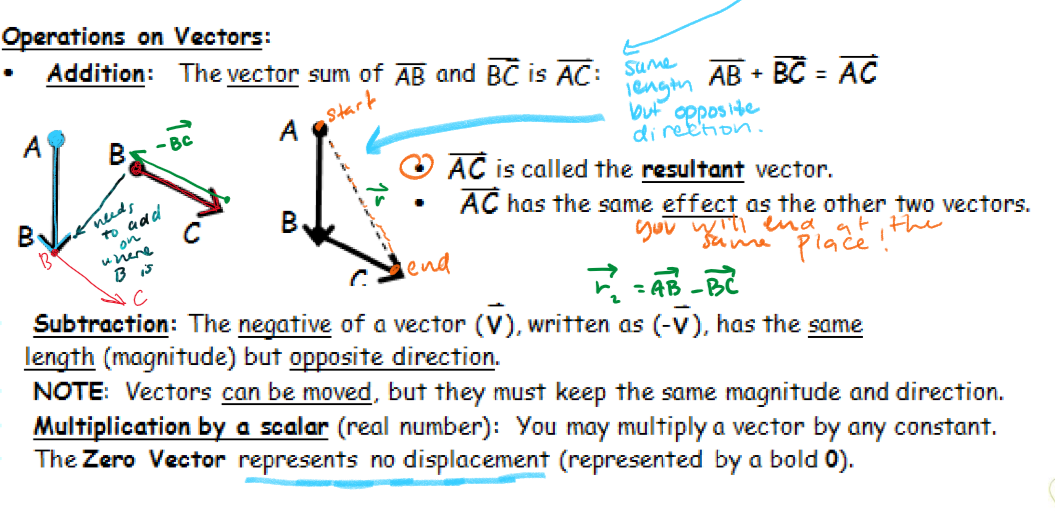
addition on vectors

sum of vector AB and BC is AC. AC is the resultant vector ( r ) and has the same effect as the other two vectors

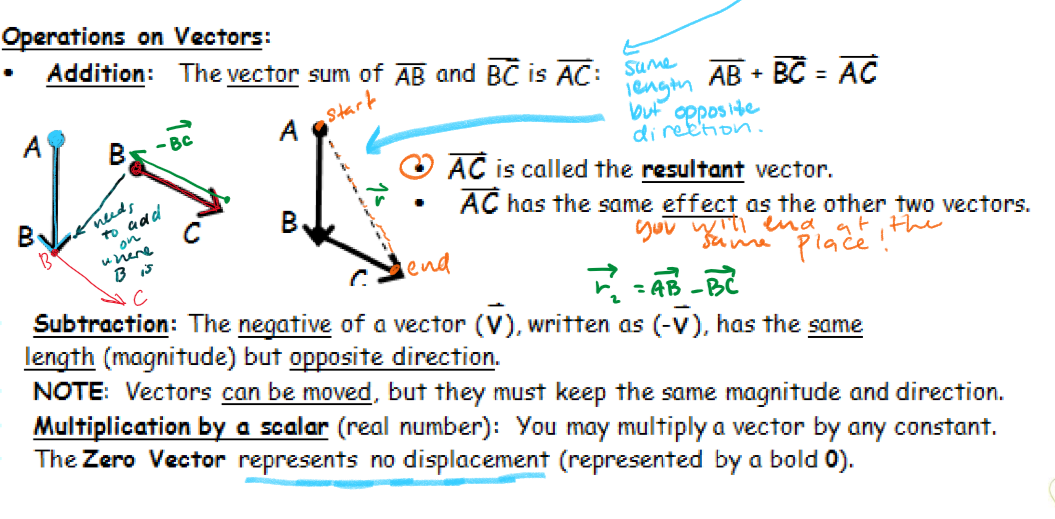
subtraction on vectors

the negative of a vector is (-v) with an arrow. it has the same LENGTH (magnitude) but OPPOSITE direction

multiplication by a scalar

you can multiply a vector by any constant

bearing vs direction angle

bearing is clockwise from north, direction angle is counterclockwise from positive x-axis

component form of a vector

a vector is in standard position if its initial point is at the origin (0,0). the components of a vector are found by projecting the vector onto the coordinate axis in standard position.

example of component form: <7,4>

v= <a,b>, with a being horizontal and b being vertical component

displacement

final position - initial position of a vector

calculating magnitude of a vector algebraically

(||v||)² aka magnitude = x² + y² (horizontal and vertical components) basically right triangle trig

algebraic operations on vectors

if you know your <a,b> you can easily use these formulas!

if u = <a1, b1> and v= <a2, b2>:

u + v = <a1+a2, b1+b2>

u - v = <a1-a2, b1-b2>

cu (multiplying vector by a scalar) = <ca1, cb1>

vectors in terms of i and j

the unit vectors, i and j have a magnitude of one.

v = <a, b> = ai +bj

ex: 7i + 4j

unit vector

creating a unit vector from another vector v is called normalizing the vector

formula: u = v/||v||

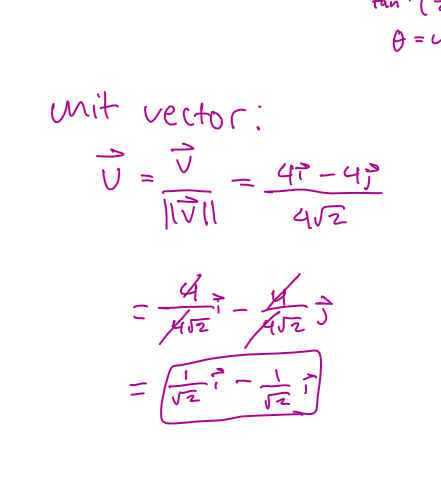
equilibrant vector

opposite of a result vector. balances a combination of vectors such that the sum of the vectors and the equilibrant vector is the zero vector

formula: the equilibrant vector of a+b is -(a+b)

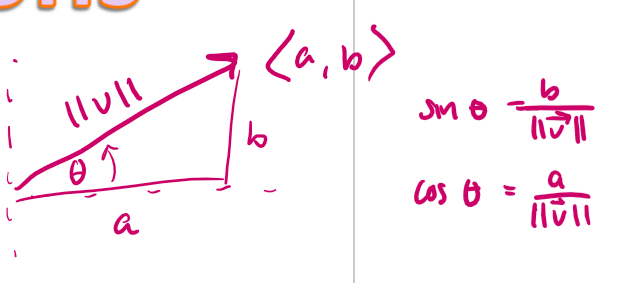
horizontal and vertical components of a vector

<a, b> basically

dot product

get hype

angle between two vectors/dot product theorem

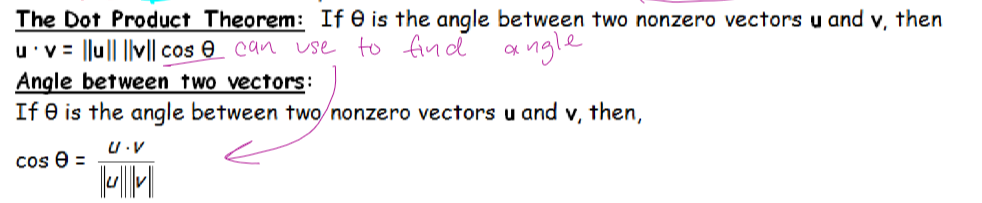
orthogonal vectors

two vectors that are perpendicular if (u)(v) = 0. so basically use the dot product and you can see if its zero

parametric form to rectangular form

trick—use sin²t + cos²t = 1!!

standard form of parametrics…

x=AcosBt

y=AsinBt

if A is same for both x and y, it will make a circle!

• square eqs

• add them

• factor out GCF

• substitute in 1

rectangular form to parametric form

explain how to do this

explain how to do this

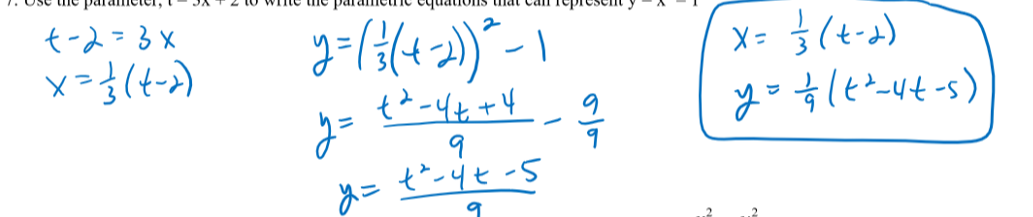
explain how to do this