E&M

What is Capacitance?

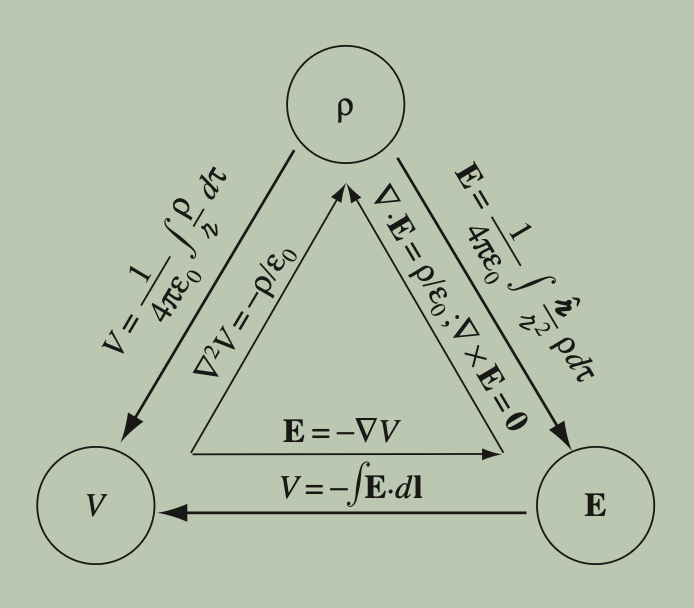
Capacitance is the ability of a system to store an electric charge, measured in farads. It is defined as the ratio of the electric charge stored to the potential difference across the plates of a capacitor.

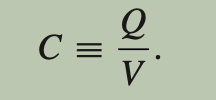
Why do we choose to make our reference point for potential at infinity

Potential drops off with distance. Setting the reference point at infinity allows all observers to consider the potential to be zero, simplifying calculations. This convention makes it easier to compare potentials at different points in space.

How do we prove the E = -∇ V?

Use the relationship that potential at a certain point is the negative line integral of the E-field from the reference point to r. Potential difference from point b (V(b) - V(a)) is given by the difference of those two integrals or the integral over the E-field from point a to point b, which through the Fundamental Theorem for Gradients leads to the equation E = -∇ V. This coincides with out intuition that force is also the negative gradient of potential energy.

What is an equipotential region.

An equipotential field is a region in which all points have the same electric potential, meaning that no work is required to move a charge within that field. Electric field lines are always perpendicular to equipotential surfaces.

What is Poisson’s Equation and where does it come from?

Poisson’s Equation says that the Laplacian (second gradient) of the electric potential V is proportional to the charge density ρ. It is derived from Gauss's Law and relates the electric field to the distribution of charge in space. (∇² V= -ρ/ε₀)

What is Laplace’s Equation and where does it come from?

Laplace’s Equation is a special case of Poisson’s equation. It states that the Laplacian of the electric potential V is equal to zero (∇²V = 0). It arises in regions where there are no charges present, indicating that the electric potential is harmonic in those areas.

What can we say about the potential at any given point in a region with a potential that satisfies Laplace’s Equation? ∇² V = 0?

V is equal to the average of the potential values on a small sphere (or circle, in 2D) centered at that point. This is called the Mean Value Property of harmonic functions.

What is Coulomb’s Law

Coulomb’s law says that the force on a charge due to a charge is proportional to the product of the magnitudes of the charges and inversely proportional to the squared distance between them.

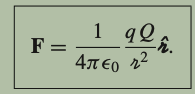
What is Coulomb’s Law in General for the field of a uniform charge distribution.

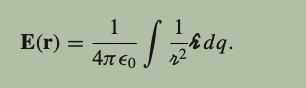
What is the Potential for a volume charge?

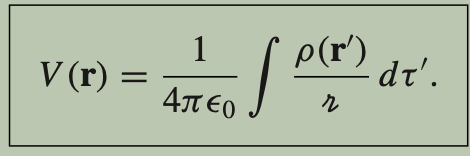
What is the general relation between the potential difference between two points and work done to move a charge between them?

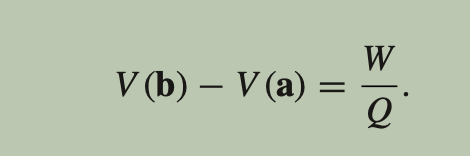
What is the Energy in a point charge distribution? (using distinct charges)

Equivalent to the work done to bring each charge into its position from infinity, calculated using potential energy.

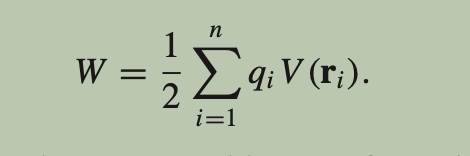
What is the energy in a continuous charge distribution? (using charge density)

The energy in a continuous charge distribution is found by integrating the potential energy contributions from each infinitesimal charge element, taking into account the distances between all pairs of charges.

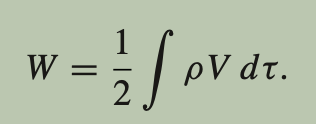
What is the energy in a continuous charge distribution? (using electric field)

The total energy stored in the electric field of a continuous charge distribution, calculated by integrating the energy density over the volume of the charge distribution.

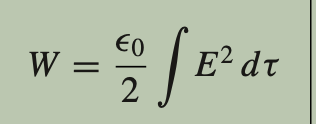
Charge, Potential, Field Relation Chart

What is the point of multipole expansion?

Multipole expansion allows us to approximate the electric potential of a charge distribution when observed from far away We express it as a series of simpler point charge terms, such as monopoles, dipoles, and quadrupoles, facilitating calculations at large distances. Essentially a superposition of multiple different spacial patterns of the charge distribution.

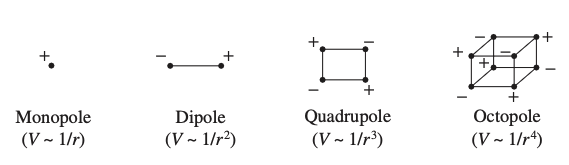
When is it ok to use Multipole Expansion?

When we are observing a charge distribution from far away. AKA when the observation distance is significantly larger than the charge distribution itself.

What is a multipole moment?

A measure of the distribution of charge in a system, representing how charge is arranged in relation to a reference point. Multipole moments include monopole, dipole, quadrupole, and higher-order terms, each describing different characteristics of the charge configuration. 

Dipole moment formulas?

This is the formulas for dipole moment for a continuous distribution or an arrangement of charges. This is the main thing to remember because to find potential you'll use this to find the dipole potential contribution, quadrupole and up get significantly less simple.

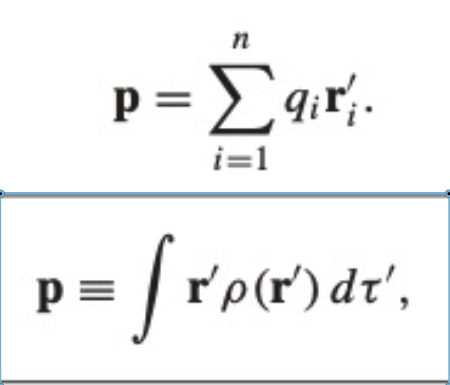
What are Dielectrics?

Materials that polarize in an electric field, affecting capacitance and electric field distribution.

What is atomic polarizability?

A measure of how much the electron cloud of an atom can be distorted by an external electric field, influencing the atom's overall polarizability and interaction with electric fields. Intuition: atomic polarizability is a vector value so atoms are more easily distorted in some directions than other leading to anisotropic behavior in their interaction with electric fields.