Stars

Why are most land telescopes in optical or radio?

The atmosphere blocks all other wavelengths

Bolometric

measured across all wavelengths

Bandpass

range of wavelength

Distance modulus equation

Planck’s law for BB radiation

When graphed, total energy = area under curve

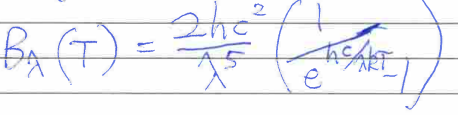
How many steradians in a sphere?

4π

Rate of detections at a detector from a point source propagating as a sphere

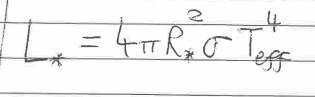
Luminosity of a star

Effective temperature of the sun

5781K

In real stellar spectra, what causes continuum, emission and absorption lines?

• continuum produced by thermal emission from dense gas

• emission lines produced by the decay to lower states of electrons that moved to higher states in hot gas by temperature and collisions

• absorption lines produced from a electrons in a cooler gas absorbing and re-emitting photons from the star

H transition lines

• Lyman (to ground state)

• Balmer (to n=2)

• Paschen (to n=3)

The spectral classes of stars

-O-B-A-F-G-K-M

-based on temperature (O hottest, M coolest)

-subdivisions e.g. G0-G9 (0 hot end, 9 cool end)

Why do H lines fade for hot stars but He are still seen?

-H ionised so no absorption lines

-He has very tightly bound electrons, so high T required to raise them from ground state. Allows absorption at visible wavelengths.

What stars are molecular lines seen in?

Cooler stars

What stars are metal lines seen in?

Sun-like stars

How does the luminosity classification of stars work?

-higher gravity changes width

-changes luminosity

-gives information of radius

Factors controlling line strength

• Excitation

• Ionisation

Quantum numbers defining quantum states

• n = energy

• l = ang. mom.

• m_l = alignment

• m_s = spin

Boltzmann Equation

g_A = number of states with energy E_A

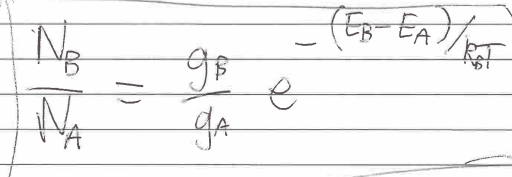
Ratio of number of electrons in energy state m to total number of electrons in all states

U(T) partition function

Saha equation

N_i = number of particles in ionisation state 1

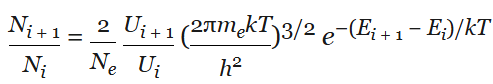
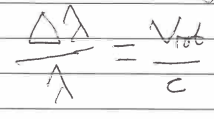
Ratio of intensity at distance z to intensity at z = 0

Mean free path for a photon to travel

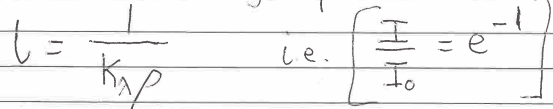
Optical depth

Often interpreted as how far we can see into a material

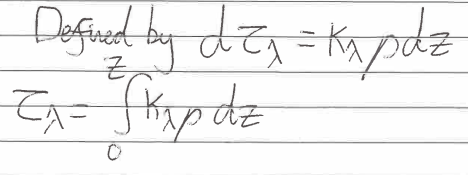
Sources of opacity

• bound-bound transitions

• bound free absorption

• free-free absorption

• scattering

Bound-free absorption

• ionisation

• each state has a smooth linear spectrum with a cut off

Free-Free absorption

• free electron absorbing photon

• follows Kramer’s Law

Scattering

• Rayleigh scattering with atoms and low energy photons. Elastic

• Compton scattering on electrons. Inelastic

• Thomson scattering on electrons. Elastic. Low energy limit of Compton

Line broadening

• lines in spectra should ideally be infinitely thin

• instead they have thickness

Line broadening by natural broadening

• from uncertainty principle

• electron in excited state for finite time so can only have uncertain value

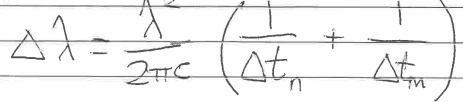
Line broadening by Doppler broadening

from motion of absorbing atom

Line Broadening by pressure broadening

• uncertainty principle again

• collisions shorten electron lifetime in state

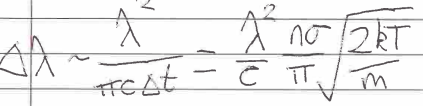
Line broadening by stellar rotation

constant doppler shift from rotating star

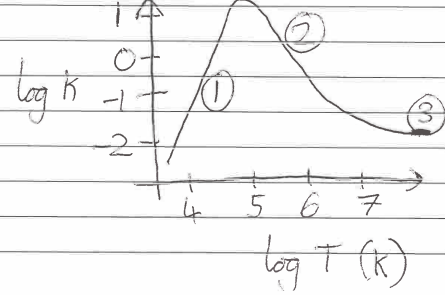
Combined opacity spectrum sections

• 1) H^- opacity, steep rise as number of free electrons rises with T

• 2) Follows Kramer’s Law, driven by b-f and f-f absorption

• 3) all electrons free, converges to Thomson scattering coefficient

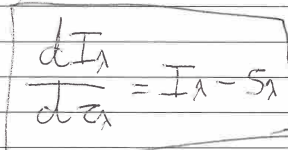
Radiative transfer equation

Local thermal equilibrium

• T constant in region

• velocity distribution follows Maxwell-Boltzmann

• photon mean free path small

• Optically thick, T non zero so LTE is BB

How does local thermal equilibrium explain emission and absorption lines?

• emission: hot gas, not dense enough for pure BB

• absorption: dense BB emitter with cold gas in front

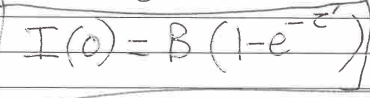
Radiation pressure equation

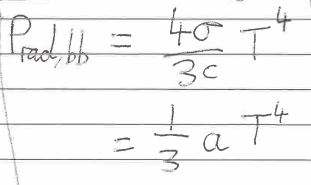
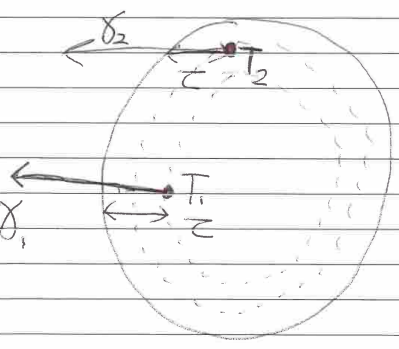
Temperature profile of star

‘surface’ we see is at optical density of 2/3

Limb darkening

• at star’s edges, we see cooler T

• redder wavelength

• less intensity

Hydrostatic equilibrium equation

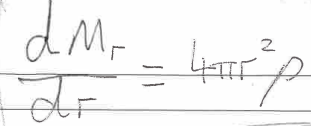
Mass conservation equation

Energy generation conservation equation

ε = energy generation rate per unit mass

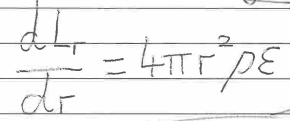
Energy transport through radiation equation

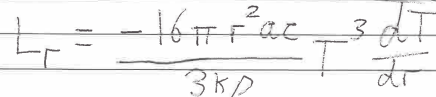
Schwarzschild criterion for stability

Virial Theorem

Timescale =

quantity / rate of change

Gravitational timescale

Thermal timescale

Nuclear timescale

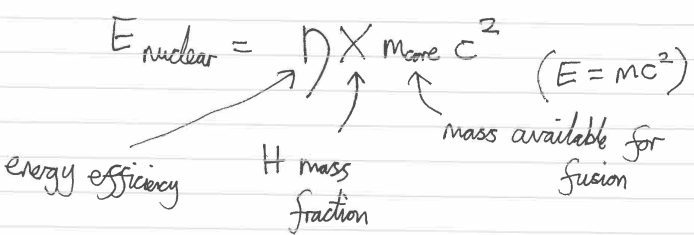
PP1 chain for Hydrogen fusion

• ¹H —> ²H + e⁺ + v_e

• ²H + ¹H —> ³He + γ

• 2 ³He —> ⁴He + 2 ¹H

Deuterium formed from beta decay of 1p to 1n

Issue with the fusion process and how it is overcome

• thermal energy must be enough to overcome coulomb force for fusion

• required temperature is higher than actual temperature of the sun

• overcome by quantum tunnelling

What do stars form from?

Gravitational collapse of clouds of material

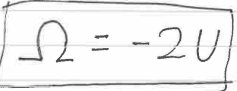
Virial theorem:

• 2U > |Ω| cloud expands

• 2U < |Ω| cloud collapses

Gravitational potential of cloud

Jeans mass required for cloud collapse

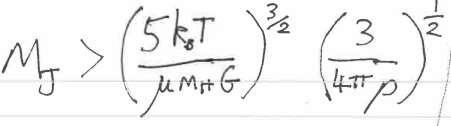
Initial mass function of stars details

• all stars born from the same cloud have same mass distribution proportional to M^a

• If exponent < 0, more low mass stars due to cloud fragment

• massive stars have higher L so produce more of the observed light

Protostars details

• cloud collapses to pre-main sequence star after ~ 10⁶ yr

• must conserve angular momentum through accretion disk, jets and rotation

• Deuterium burning after collapse forms protostar ~10⁷ yr after collapse

Main sequence details

• H fusion through PP chains

• He builds up in core

• supported by radiation pressure

• ~ 7 Gyr for Sun

Star clusters

• stars formed from the same cloud

• same age

• similar composition

• same distance

• very useful in observing stellar evolution

Blue stragglers

• stars that break HR model

• binaries

• results of stellar mergers

Subgiant branch

• core exhausted H

• H burning shell feeds core He

• grows until thermal pressure can’t support it

• eventually, core contracts and becomes degenerate

Red Giant branch

• core contracts from increased mass

• envelope expands

• luminosity increases with core and shell temp

• radius increases

• effective temp decreases

Helium flash

• end of RGB, core is degenerate

• no regulation so runaway fusion

• He fusion ignites core in a few seconds

• energy released comparable to a galaxy, mostly absorbed by outer layers

• ends when degeneracy lifted

Horizontal branch

• core He burning to C + O

• H burning shell

• Temp of Horizontal branch about 10% of main sequence temp

Asymptotic giant branch (AGB)

• He burning in shell leads to H shell expansion, cooling H shell so less H fusion

• He depletes, H shell reignites, deposits He on shell below and reignites He fusion

• Giant convective envelope formed, ejected by superwinds

• leaves a degenerate C+O core for M >~ 8 M☉

Post AGB

• planetary nebula from ejected material

• exposed hot C + O core

• white dwarf

Post AGB for higher mass stars

• similar but faster than low mass stars until AGB

• no He flash

• Fusion continues C - O - Si - Fe

• Fe stable, shell forms

• core collapse if above Chandrasekhar limit

• supernova

Steps to a supernova

• gravitational collapse, free fall timescale

• inner core collapse

• strong nuclear force causes bounce back

• 1% energy released as kinetic, rest as neutrinos

Remnants of a supernova

• for stars M <~ 25M☉, neutron star

• much more massive stars leave black hole

Scaling law for low mass stars

μ = average mass per particle in the core

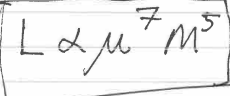
Binary stars

• formed from large molecular clouds

• 50% of sun like stars are in binaries

• rises to 100% for O type

Visual binaries

• see both components

• can track orbits

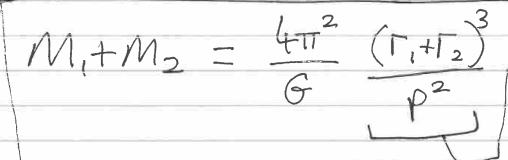
Spectroscopic binaries

• evidence of binary in spectra

• e.g. two sets of absorption lines, Doppler shift of lines

Eclipsing binaries

• one star can block light from other

• measure radii from light curve

• with spectroscopy, we get R and M