biostats - unit 2

inferential statistics

determine how close our sample estimates are to our population parameters

null hypothesis

a specific statement about a population made for the sake of argument

• typically says there’s no difference between the true value of a population and hypothesized value or no difference between 2+ samples drawn from a population

alternative hypothesis

states that our parameter estimate is different from null hypothesis

• hypothesis that parameters are influenced by non-random cause

two-tailed test

no direction of alternative hypothesis, either outcome is tested/possible

one-tailed test

direction of hypothesis is predicted (need good reason for one-tailed test)

binomial exact test

use to determine if observed proportion of successes in a sample differs significantly from hypothesized population proportion

test-statistic

single, standardized measure of a sample distribution

• allows us to evaluate how comparable our sample is to what we would expect under the null hypothesis

null distribution

sampling distribution of the test statistic if the null hypothesis were true

why is null distribution

tells you whether something interesting is going on or not!!

key to understanding all statistical tests and p-values

• if test-statistic falls in the middle of null distribution, you can assume nothing special is happening (fail to reject null hypothesis)

p-value

probability of obtaining test-statistic or more extreme values if the null hypothesis is true

interpretation if p-value is 0.031

3.1% of the time, if p = 0.5 in a population of toads, we would expect to obtain 14 or more righties or lefties in a sample of 18 toads —> therefore, our sample seems unlikely if Ho is true

significance level

probability used as the threshold for rejecting the null hypothesis

• if p-value is =< threshold value, we find support for Ha and can say result is “statistically significant” —> reject Ho

critical value

value of a test-statistic required to achieve P =< threshold value

type I error

mistakenly rejecting a true null, false positive

• occurs with probability threshold value

why can’t we just lower our threshold value to prevent type I errors?

almost no chance any sample could lead to rejection of null and would cause us to routinely fail to reject false null hypotheses

type II error

false negative, mistakenly accepting a false null

• keeps us from setting threshold value too low

  • depends on sample size, effect size, and precision —> more difficult to estimate

ecological/biological hypothesis

what is the mechanism we think underlies the difference we expect to see

exploratory analysis

goal is to find the story of the data

explanatory analysis

goal is to share the story of the data

goal of two variable comparisons

visualize the association between variables

numeric vs numeric

scatterplot

categorical vs numeric

mean and error bars or boxplots

contingency table

frequency of occurence of all combinations of 2 or more variables

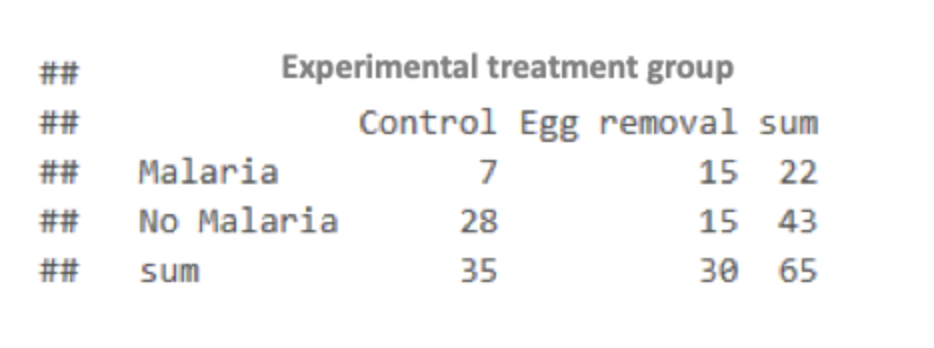
categorical vs categorical

• contingency table

• grouped bar graph

• mosaic plot

correlation

correlation coefficient (r ) measures the strength and direction of the association between 2 numerical variables

• no implications of causality (no explanatory or response variables)

regression

measures the functional/causal relationship between two variables

• gives us fit line (incorporates correlation and slope)

regression - big slope but small correlation

when x changes, y changes a lot BUT pattern isn’t reliable (very noisy)

finding line of best fit for regression

from sum of squares (think: variance)

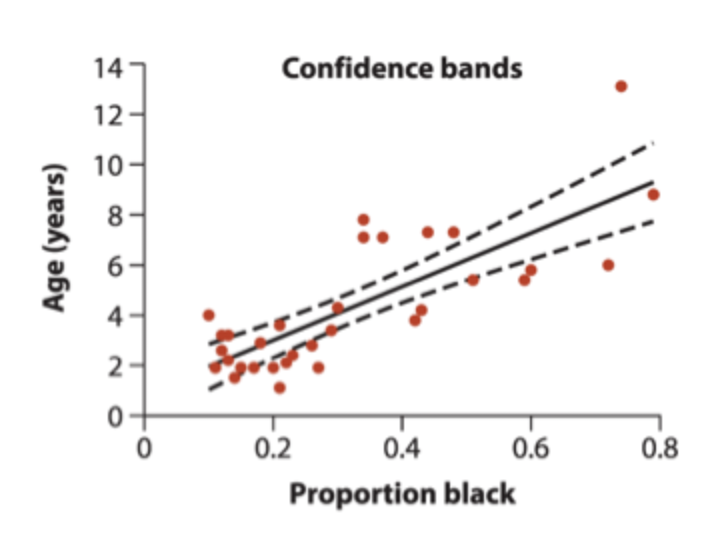
regression - confidence bands

measure precision of the predicted Y for each value of x

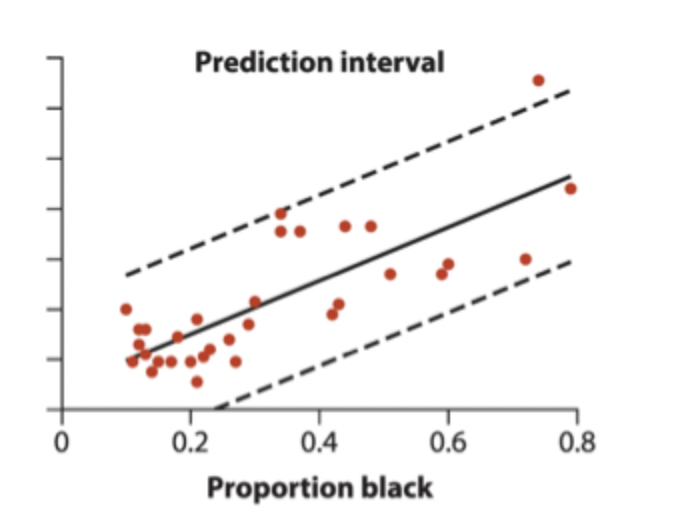
regression - prediction intervals

measures the precision of a single predicted y-value for each X

what we report for regression

r², F-statistic, and p-value

t-tests and ANOVAs

both compare difference between groups, so predictor is categorical and each category is a different group

t-test

is our sample mean more than two 1.96 SE away from null distribution parameter mean? if so, we would only expect to see that data 5% of the time

ANOVA

is the amount of variability in each group greater than the amount of variability between the group means?

F-distribution

null distribution of F-statistic, skewed right, all non-negative values (because variances can’t be negative)

ANOVA and F-distribution

if F-statistic from ANOVA falls in tail of F-distribution - reject null hypothesis

• f-statistic comes from comparing among to within group variances to detect differences in group means

  • F > 1 = more difference between treatment groups than variation within groups

  • F = 1 means equal among and within group variance

what we report for t-test

t-statistic, p-value, and df

what we report for ANOVA

F-statistic, df, and p-value

when to use t-test or ANOVA

categorical predictor and numerical response

when to use x²

categorical predictor and categorical response

goal of x²

what is the observed ratio of members of each group? does it differ from expected ratio?

are the two categorical variables independent of each other?

x² distribution

frequency distribution of x² under a null hypothesis predicting expected categorical counts

• not symmetric and right skewed

• all non-negative values

what we report for x²

x², df, and p-value

parametric assumptions

• random, independent sampling and sufficient sample size

• normality

• homoscedasticity

• no outliers

requirements for x² test

all expected values greater than 1 and 80% greater than 5

testing for normality

visualization of residuals (histogram) or shapiro-wilk test

shapiro-wilk

p-value has to be greater than 0.05 to indicate that the data is normal

testing for homoscedasticity

look at actual values of raw data, look at residuals vs fitted plots (dotted line should be approximately horizontal)

• use levene’s test

homoscedasticity

one group should not be much more variable than the others

power of log transformations

helps with right skew, outliers, and heteroscedasticity

why are transformations like log permitted

still preserves the relationship in the data, it just rescales it to make things behave better

non parametric tests

• less powerful so you’re more likely to miss a real difference

• much harder to interpret biologically

why it’s important to start with a thorough visualization of data

if you start out by only testing one hypothesis, you could get tunnel vision and miss finding something really important

• data visualization opens your mind so you don’t miss important patterns, weird shapes, outliers, etc.

QQ plot

visualize normality

residuals vs fitted values

visualize heteroscedasticity

Post-ANOVA analysis for fixed effects

planned comparisons and unplanned comparisons

syntax for t-test

t.test(y ~ x, data = dataName) OR t.test(Data$Var1, Data$Var2, paired = TRUE)

calculating expected for chi squared test

chisq.test(fish_table)$expected

syntax for chi squared test

chisq.test(fish_table, correct = FALSE)

planned comparisons

focus in on a few scientifically sensible comparisons. You can't decide which comparisons to do after looking at the data. The choice must be based on the scientific questions you are asking, and be chosen when you design the experiment

unplanned comparisons

post hoc tests

testing differences between all pairs of group means while providing protection against rising Type I errors that would result from multiple comparisons

Q-Q plot

plots theoretical distribution values against residuals

scale-location homoscedasticity

checks the assumption of equal variances

histogram of residuals

checks the assumption of normality looking at results from sum-of-squares line

linearity

checks the relationship between fitted values and residuals