Business Statistics Formulas and there purposes (Exam #2)

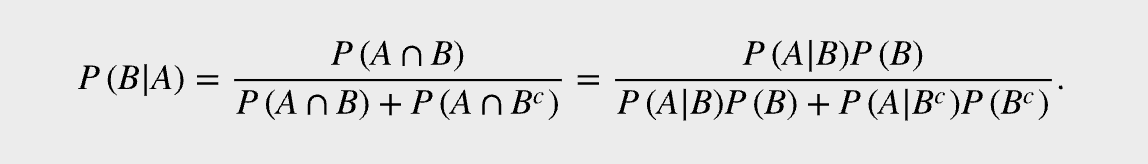
1. Bayes' Theorem

Use When:

• You are reversing conditional probability

• Given a test result or evidence, find the probability of the cause

• Common in medical testing, classification, true/false positive scenarios

Example:
You test positive for a disease. Given the accuracy of the test and the probability someone actually has the disease, what is the chance you actually have it?

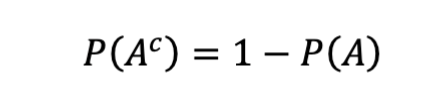
2. Complement Rule

Use When:

• It’s easier to calculate the probability something does NOT happen

• Used in almost all distributions

Example:
Probability it rains today is 0.3 → probability it doesn’t rain is 1 − 0.3 = 0.7.

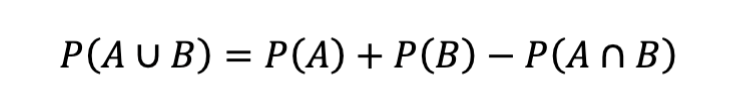
Union of Two Events

Use When:

• You want probability that at least one of two events happens

• Applies in general probability (not tied to one distribution)

Example:
P(student plays soccer) = 0.4, P(student plays basketball) = 0.3, P(both) = 0.1
→ P(plays either) = 0.4 + 0.3 − 0.1 = 0.6

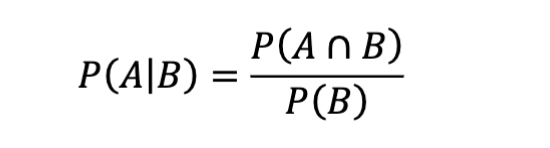
4. Conditional Probability

Use When:

• You already know event B happened and want the chance A also happened

• Used in dependent probability questions

Example:
Probability someone is left-handed (A) given they are an artist (B).

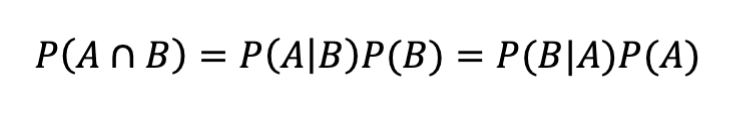
5. Multiplication Rule

Use When:

• You need the probability of both events happening

• Can be for dependent or independent events

Example:
Probability a randomly selected person is both female and left-handed.

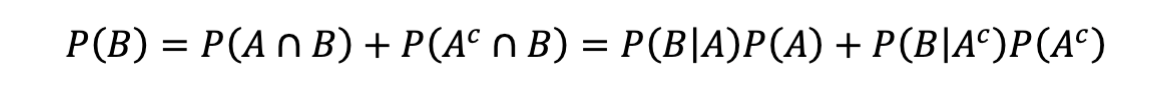
Law of Total Probability

Use When:

• You are finding the total chance of an event, considering multiple scenarios

• Often paired with Bayes’ theorem

Example:
Two machines produce parts. Machine 1 produces 70% of parts with a 2% defect rate; Machine 2 produces 30% of parts with a 4% defect rate. What is the chance a part is defective overall?

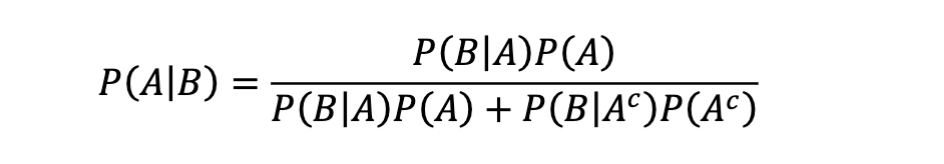
Bayes’ in A|B Form

Use When:

• Same as Bayes’ theorem, but solving for P(A∣B)

• Used for "given the evidence, find the cause"

Example:
A patient tests positive. What’s probability they actually have the disease?

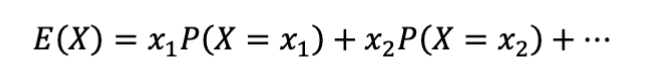
Expected Value of Discrete Random Variable

Use When:

• For discrete distributions like Binomial, Geometric

• Represents average outcome

Example:
Roll a weighted die where 6 has higher probability. Expected roll value uses this formula.

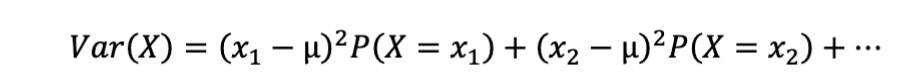
9. Variance

Use When:

• Measures how spread out the outcomes are

• Same distributions as expected value

Example:
Variance of rolling a die.

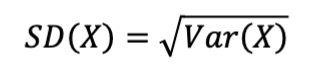
10. Standard Deviation

Use When:

• Always! Standard deviation is just the square root of variance

• Used to measure spread in any distribution

Example:
If variance = 4 → SD = √4 = 2.

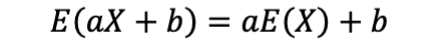
Linear Transformation of Expected Value

Use When:

• You apply a linear transformation to a random variable (like converting Celsius to Fahrenheit).
  Example:
  If E(X)=50and you convert scores with Y=2X+10Y, then E(Y)=2(50)+10=110

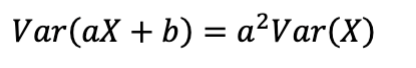
Linear Transformation of Variance

Use When:

• Measure how scaling affects spread; adding a constant does not affect variance.
  Example:
  If Var(X)=4 and Y=3X+2Y, then Var(Y)=32⋅4=36 Var(Y) = 3^2 x 4 = 36

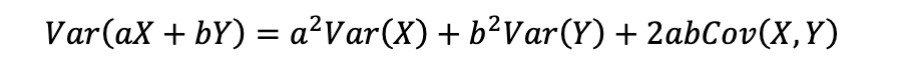
Use When:

• Assessing combined variability; covariance captures correlation.
  Example:
  Used in finance to calculate risk of a two-asset portfolio.

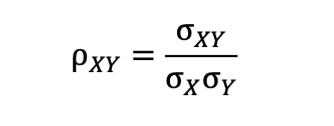
Use When:

• To measure strength and direction of linear relationship between two variables.
  Example:
  Height and weight: if ρ=0.8\rho=0.8ρ=0.8, strong positive linear correlation.

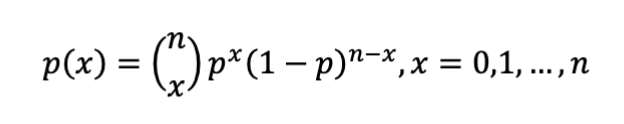
Use When:

• Fixed number of trials

• Two outcomes (success/failure)

• Independent trials

• Constant probability
  Example:
  Flip a coin 5 times: probability of exactly 2 heads.

Mean & Variance:

E(X)=np Var(X)=np(1−p)

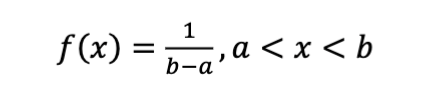
PDF Formula:

Use When:

• All outcomes in an interval are equally likely

• Models random time or location within a range
  Example:
  Bus arrives randomly between 0 and 10 minutes → uniform(0,10).

Mean & Variance 

E(X)=a+b/2​  Var(X)=(b−a)²/12

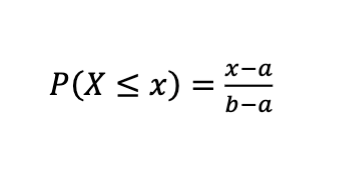
Uniform Distribution Cumulative Probability

Use When:

The random variable X is uniformly distributed on the interval [a,b]

• You're asked for the probability that X is less than or equal to some value x.

Example:
Bus arrives uniformly between 0 and 10 minutes. What is the probability it arrives in 4 minutes or less?

P(X≤4)=4−0/ 10−0=0.4 

✅ Interpretation: 40% chance the bus arrives within 4 minutes.

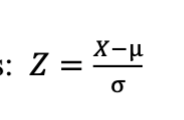
Z-score (Standard Normal Transformation)

Use When:

• You want to convert a value from a normal distribution into a standard normal distribution (mean = 0, SD = 1).

• Used to find probabilities using the Z-table or to compare values across different distributions.

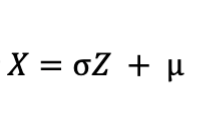
Converting From Z Back to X

Use When:

• You are given a Z-score (often from a percentile) and need to find the actual value in the original distribution.