3 Meccanica razionale Capitolo3: cinematica dei sistemi e delle masse

definizione di sistema libero

un sistema in cui bisogna conoscere tutte le coordinate dei punti per conoscere la configuarione del sistema

definizione di vincolo

un vincolo è una funzioen che correla e limita le posizione e/o gli spostamenti di un sistema meccanico

come vengono classificati i vincoli

1. vincoli olonomi e anolonomi

2. vincoli interni e esterni

3. vincoli unilaterali e bilaterali

4. vincoli reonomi e scleronomi

5. vincoli lisci e scabri

che cosa è un sistema olonomo

un sistema solamente soggetto a vincoli olonomi

definire i vincoli esterni ed interni
che cosa differenziano
fare esempi

la introduzinoi di questo tipo di vincolo è stata fatta perchè si distingue fra vincoli interni o allinterno dello stesso sistema come i vincoli di rigidità e vincoli esterni che sorgono quando si interfaccia il sistema con l’ambiente

ES: vincoli interni: condizione di rigidità
vincoli esterni: condizioni tra sistemi come rotolamento

che cosa sono i vincoli olonomi e anolonomi, perche sono stati introdotti e come si fa la distinzione

la classificazione piu importante dei vincoli

• vincolo OLONOMO
  un vincolo tra le coordinate dei punti di un sistema, formato da equazioni e disequazioni in termini finiti,
  
  in altre parole:
  vincolo delle posizioni del sistema e degli spostamenti del sistema
  ES: appartenenza di un punto ad un piano,
  con le disequazioni anche: es appartenenza di un punto 1 quadrante del sistema di riferimento

• vincoli ANOLONOMI
  un vincolo che si presenta come forma differenziale non esatta, percio non integrabile
  
  il vincolo esprime vincoli per gli spostamenti del sistema ma non per le posizioni, dato che non si puo integrare
  ES: condizione di puro rotolamento: dS^(a) = dS^(r)

  • cè anche un caso particolare un vincolo pseudo anolonomi
    vicolo che sono differenziabili e riconducibili a vincoli olonomi per integrazione,
    es: disco che rotola senza strisciare su una retta
    qui la condizione di rotolamento puro è dS = dx, con dS = R*dϑ
    qui si puo integrare e si ottiene la forma R ϑ = x − x0
    

spiegare i vincoli unilaterali - bilaterali, che cosa descrivono?

• unilaterali, vincoli che contengono almeno una disuguaglianza

• bilaterali, vincoli che contengono solo uguaglianze

ES. vincolo unilaterale: un punto che è vincolato a muoversi lungo il semiasse positivo delle x:

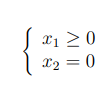
che cosa sono le posizioni di confine

sono le posizioni limite

spiegare i vincoli scleronomi e reonomi, fare esempio

la differenza è la dipendenza dal tempo:

• vincoli scleronomi: Un vincolo si dice scleronomo quando nella sua formulazione non compare la dipendenza dal tempo (dipendenza esplicita)

• vincolo reonomo: Un vincolo si dice reonomo quando nella sua formulazione compare la dipendenza esplicita dal tempo

ES: un vincolo olonomo reonomo, un punto vincolato ad appartenere ad una superficie variabile nel tempo, es disegno un punto su un pallocino e lo gonfio

come si calcola il numero di gradi di libertà di un sistema olonomo

un sistema costituito da n punti Ps s=1…n e avendo m condizioni di vincoli. allora i gradi di libertà si calcolano come 3n-m o la differenza tra gradi di libertà del sistema libero e condizioni di vincolo

definizione di grado di libertà
definizione di parametri lagrangiani

i gradi di libertà è un numero, che identifica il numero di variabili indipendenti che in un certo istante identifica univocamente la configurazione del sistema

i parametri lagrangiani sono le suddette variabili indipendenti che in un cert istante identificano univocamente la configurazione di un sistema

dimostrare che se un punto è vincolato a muoversi su una superficie, allora gli spostamenti validi sono solo quelli tangenti alla superficie stessa

che cosa è lo spazio delle configurazioni
che cosa è lo spazio degli eventi e quale è la differenza

parto da un sistema olonomo con N gradi di libertà, percio la configurazione del sistema puo essere univocamente descritta da N variabili indipendenti.
lo spazio delle configurazioni è uno spazio vettoriale di dimensione N dove la i-esima coordinata di un generico punto è il i-esimo parametro lagrangiano che descrive la configurazione del sistema a N gradi di libertà. percio ogni punto rappresenta una possibile configurazione del sistema

poi c’è lo spazio degli eventi, questo prende in considerazione anche il tempo come coordinata e perciò avrà N+1 dimensioni
q = (t, q₁, … , q_N)

come faccio a calcolare la velocità di un sistema olonomo

i punti di un sistema olonomo sono una funzione dei parametri lagrangiani:
OPs = OPs( q1, q2 , …, qn, t)
se ora derivo OPs rispetto al tempo ho che il s-esimo vettore velocità nel punto OPs sara:

dove la convenzione di Einstein indica una somma per gli indici ripetuti “h“

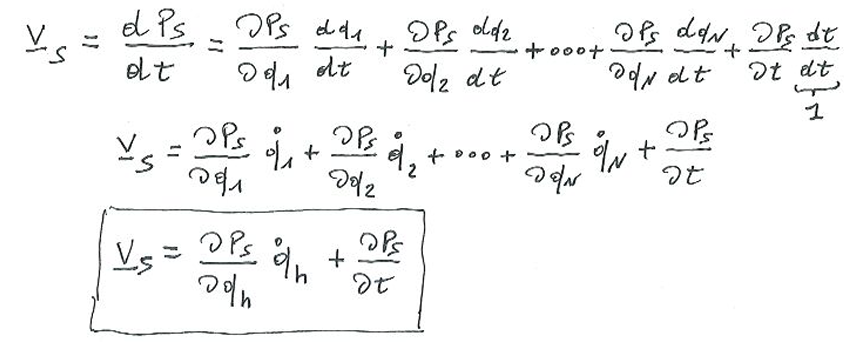
scrivere la formula di derivazione di funzioni composte in più variabili

elencare tutti i tipi di spostamento e come si rappresentano per un sistema olonomo

NOTA: la formula per differenziare una funzione composta in piu variabili è: sia f(x,y) :R² → R e
siano x(t) e y(t) funzioni a una variabile, chiamo F(t) = f(x(t),y(t)) la funzione composta, allora il differenziale di F(t) è:

dF/dt = ∂f/∂x * dx/dt + ∂f/∂y * dy/dt

1. spostamento infinitesimo, d*Ps
   puramente matematico che ignora la presenza di vincoli

2. spostamento infinitesimo possibile δPs
   spostamento infinitesimo che però tiene conto dei vincoli e della loro eventuale dipendenza dal tempo

3. spostamento infinitesimo virtuale ∂Ps
   spostamento infinitesimo che tiene conto dei vincoli ma NON della loro eventuale dipendenza dal tempo
   lo spostamento avviene in un istante

4. spostamento elementare o reale dPs
   un spostamento che avviene nell’intervallo [t, t + dt] che rispetta le leggi del moto, lo spostamento a livello fisico avviene

descrivere lo spostamento infinitesimo possibile

uno spostamento possibile è uno spostamento che tiene tiene conto dei vincoli e della loro eventuale dipendenza dal tempo
si scrive come:

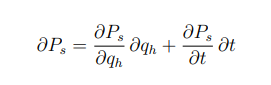
descrivere lo spostamento infinitesimo virtuale

uno spostamento infinitesimo che tiene conto dei vincoli ma non della loro dipendenza dal tempo,

il tempo viene pensato come fissato e rimane costante, si puo anche pensare che lo spostamento avviene in un istante a velocità infinita

si scrive come:

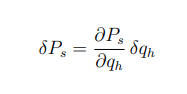
descrivere lo spostameno infinitesimo

uno spostamento che completamente ingora la presenza di vincoli

descrivere lo spostamento infinitesimo reale

uno spostamento che subisce il punto Ps nellintervallo [t,t+dt] rispettando i vincoli ed in corrispondenza ad un determinato moto.
uno spostamento che deve obbidire alle leggi del moto

quale tipo di vincoli deve avere un sistema perche gli spostamenti elementari possibili e virtuali coincidano?

serve un sistema a vincoli scleronomi

uno spostamento elementare è anche sermpre uno spostamento infinitesimo possibile,
vale il viceversa

la prima affermazione è vera, ogni spostamento elementare è anche uno spostamento possibile, ma non è detto che uno spostamento possibilie sia anche elementared

definire gli spostamenti reversibili e irreversibili

uno spostamento si dice reversibile se lo spostamento opposto a partire dalla stessa configurazione è anche elementare. senno —> irreversibile

come calcolare la quantità di moto per un punto materiale e per un sistema di punti materiali

per un punto materiale P con massa m_P la quantità di moto è pari a
Q = m*v

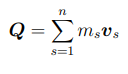
come calcolare il momento della quantità di moto di un punto materiale P di massa m rispetto ad un polo di riduzione Ω, e per un sistema di punti materiali

K = ΩP ∧ m*v

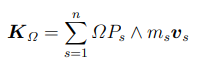
formula per la energia cinetica di un punto materiale, e per un sistema di punti materiali

T = ½ m*v²

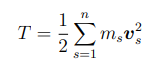
come si calcola quantità di moto, mometo della quantità di moto e energia cinetica per un sistema continuo

dQ = v*dm = v*ϱ*dC

dK = ΩP ∧ v*dm = ΩP ∧ ϱ*v*dC

dT = ½ v² *dm = ½ v² ϱ dC

integrando si ha:

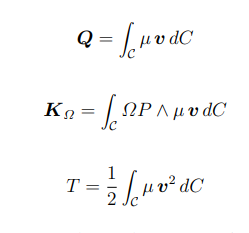
Enunciare il teorema del moto del baricentro. DIMOSTRARE

La quantità di moto di qualunque sistema materiale rispetto ad un osservatore è uguale alla quantità di moto del baricentro pensato come se fosse un punto materiale al quale viene associata la massa dell’intero sistema
Q = mv_C

che cosa dice il teorema del moto del baricentro

la quantità di moto di un qualunque sistema per un osservatore esterno equivale alla quantità di moto di un punto materiale posizionato nel baricentro del sistema e con massa uguale alla massa del sistema

enunciare il primo e il secondo teorema di König

1. Teorema di König: la energia cinetica di un sistema materiale rispetto ad un osservatore qualunque è uguale alla energia cinetica dello stesso sistema calcolata rispetto al sistema baricentrale
   sommata
   con la energia cinetica del moto del baricentro pensato come se fosse un punto materiale di massa del sistema
   T = T^(G) + ½ m*v²_Gf

2. Teorema di König: (molto simile al primo solo che al posto della energia cinetica c’è il momento della quantità di moto)
   il momento della quantità di moto di un sistema materiale rispetto ad un osservatore qualunque è uguale al momento della quantità di moto dello stesso sistema calcolata rispetto al sistema baricentrale
   sommato
   con il momento della quantità di moto del baricentro pensato come se fosse un punto materiale di massa del sistema

come è fatto un sistema di riferimento del baricentro

ha due proprietà

1. la origine coincide con il baricentro

2. gli assi del sistema baricentrale sono paralleli agli assi del sistema globale

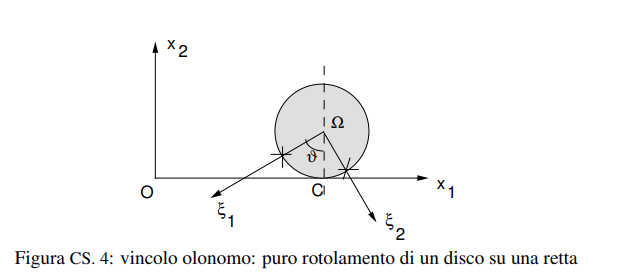
come si calcola la energia cinetica di un corpo rigido con un punto fisso?

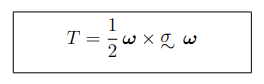
formula per calcolare la energia cinetica di un corpo rigido con asse fissa e solidale con il corpo
(NOTA per i calcoli, se serve bisogna calcolare il momento di inerzia rispetto alla asse di istantanea rotazione)

dove J è il momento di inerzia lungo l’asse fisso

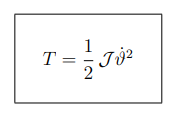
calcolare e derivare la energia cinetica di un corpo ridigo di moto rigido piano,
derivare la formula per il secondo caso

si hanno due possibilità

1. atto di moto traslatorio:
   dato che per definizione ogni punto ha la stessa velocità si avrà che:
   T = ½ m*v²

2. atto di moto rotatorio
   in questo caso esiste un asse di istantanea rotazioni ed è ortogonale al piano invariante e percio la energia cinetica del sistema si calcola come per un corpo rigido con una asse solidale

come si calcola la energia cinetica per un sistema continuo

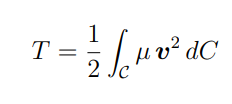
Dimostrare il primo teorema di Konig

Dimostrare il secondo teorema di König

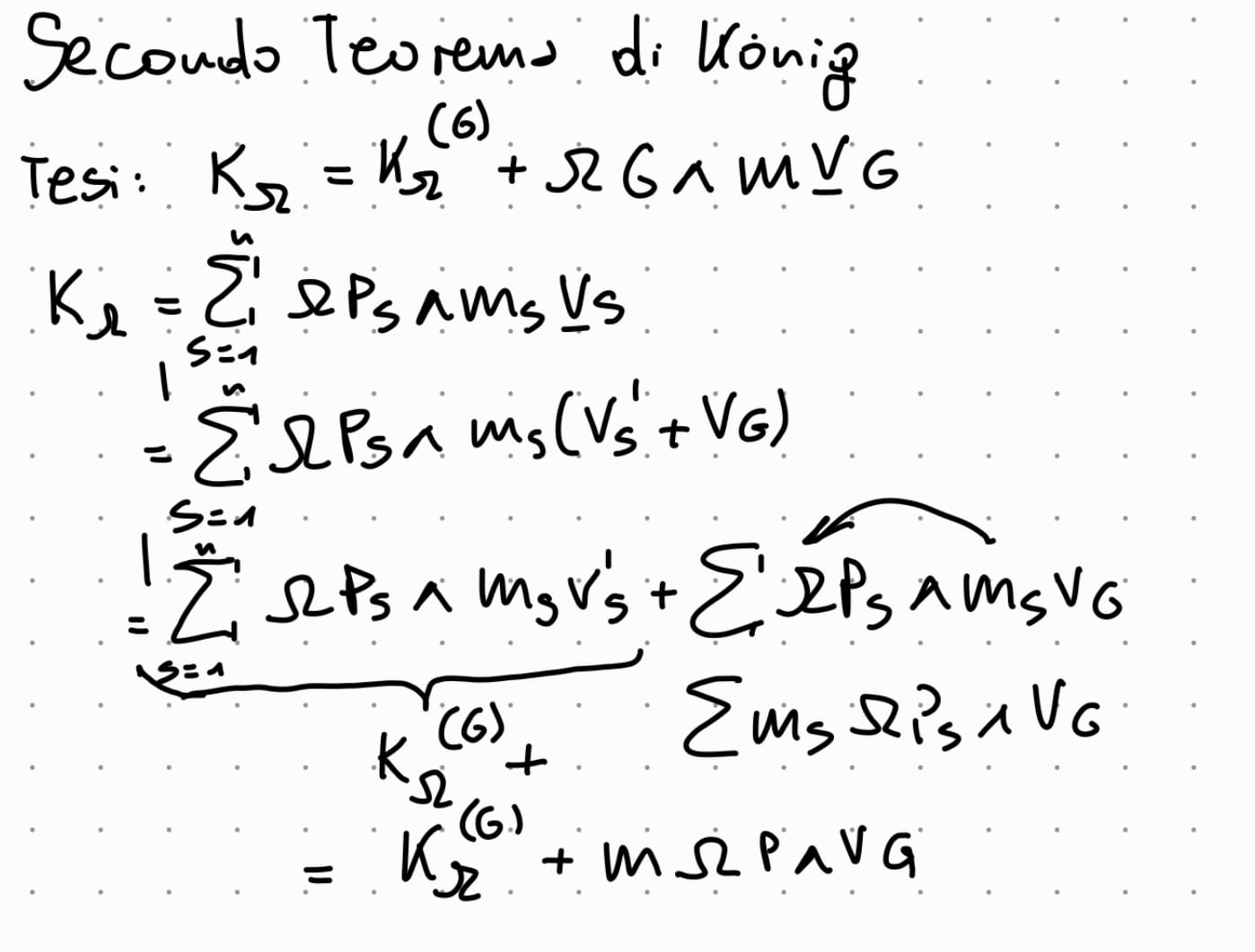
come si calcola la energia cinetica di un sistema olonomo, DERIVAZIONE FORMULA (matrice di inerzia )

come si calcola la energia cinetica di un sistema olonomo con i vincoli schleronomi (indipendenti dal tempo)

quali sono le proprietà della matrice dell’energia cinetica

1. simmertica

2. definita positiva

calcolare la matrice della energia cinetica per un sistema schleronomo a

1. 1 grado di libertà

2. 2 gradi di libertà

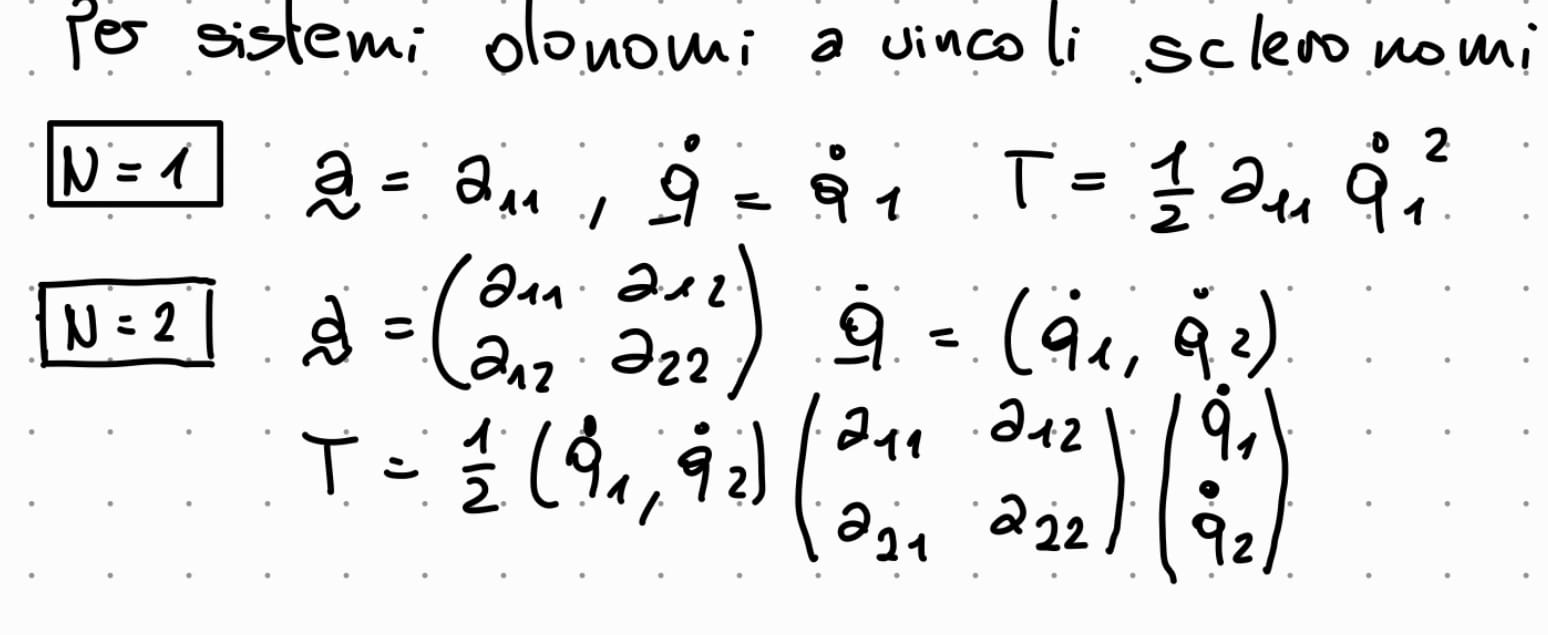
come si calcola il momento della quantità di moto di un corpo rigido che ruota attorno ad un asse,
come cambia la formula se lasse è asse principale di inerzia

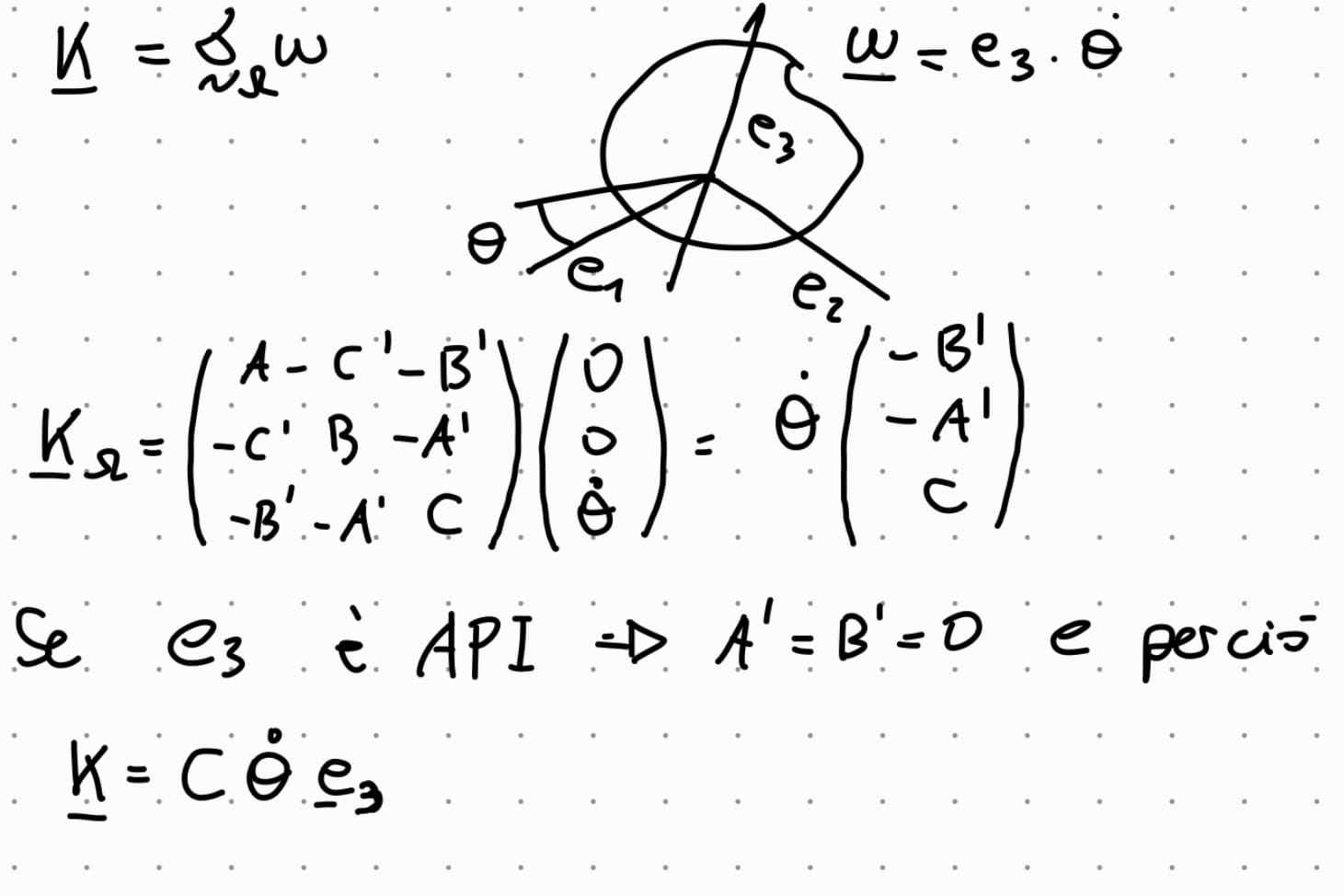
come ricavare la formula per la energia cinetica di un corpo rigido che gira attorno ad un asse