AME 209: 19. Numerical Methods in Python (NumPy and SciPy)

By the end of this section, students should be able to... • Load the correct modules to apply various numerical methods • Use root_scalar to find roots numerically • Perform 1D interpolation interp1d with different methods (e.g., linear, cubic) • Solve systems of linear equations using linalg.solve • Integrate numerically using the Riemann sums and built-in methods such as trapz and integrate.quad • Compute numerical derivatives using forward, backward, centered finite difference schemes, and the gradient function • Convert a higher order ODE to a system of first order ODEs (reduction of order) • Solve ODEs using the solve_ivp function • Convert an BVP to an IVP and combine root finding and ODE solvers

Numerical Methods

echniques used to approximate solutions to mathematical problems that can’t be solved analytically.

root_scalar()

Function from scipy.optimize used to numerically find the root of a function f(x)=0f(x) = 0f(x)=0.

Bracket (in root_scalar)

A tuple [a, b] specifying the interval in which to search for a root (used with methods like 'bisect' or 'brentq').

Method (in root_scalar)

Algorithm used for root finding: 'bisect', 'newton', 'brentq', 'secant', etc.

Bisection Method

A bracketing method that repeatedly halves the interval where a sign change occurs. Always converges but slower.

Newton-Raphson Method

A faster root-finding method that uses the derivative of the function, but requires a good initial guess and can fail to converge.

Brent’s Method

A hybrid root-finding method combining bisection, secant, and inverse quadratic interpolation—robust and fast.I

Interpolation

Estimating values between known data points.

interp1d()

Function from scipy.interpolate that creates an interpolation function from discrete data (supports 'linear', 'cubic', etc.).

Linear Interpolation

Connects data points with straight lines. Simple but may not be smooth.

Cubic Interpolation

Uses cubic polynomials between data points. Produces a smoother curve.

linalg.solve()

Function from numpy.linalg to solve systems of linear equations Ax=bAx = bAx=b.

Numerical Integration

Approximation of definite integrals using summation methods.

Riemann Sum

A basic numerical integration method using rectangles.

np.trapz()

NumPy function that performs trapezoidal rule integration for discrete data.

integrate.quad()

High-accuracy integration of continuous functions using adaptive quadrature (from scipy.integrate).

Finite Difference

Method for approximating derivatives using nearby function values.

Forward Difference

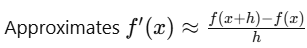
Backward Difference

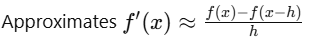
Centered Difference

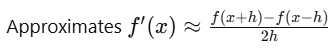
np.gradient

Function that computes numerical derivatives using centered differences by default.

ODE (Ordinary Differential Equation)

An equation involving derivatives of a function with respect to one variable.

Reduction of Order

Process of converting a higher-order ODE into a system of first-order ODEs for numerical solving.

solve_inp()

Function from scipy.integrate to numerically solve initial value problems for ODEs.

Initial Value Problem (IVP)

An ODE with specified value(s) at the start of the interval.

Boundary Value Problem (BVP)

An ODE with specified values at both ends of the interval. Often converted to IVP for numerical solving.

sol.root

Attribute of root_scalar() result: the computed root.

sol.converged

Attribute: Boolean indicating whether the method successfully found a root.

sol.flag

Attribute: String that summarizes the solver’s result (e.g., 'converged', 'convergence failure').