Year 11 maths mocks

x² × x³

x⁵

(x²)³

x²×³ = x⁶

x⁵ ÷ x²

x³

x⁰

1 (anything to the 0 power is 1)

x⁻²

-1/x²

what do negative indices mean?

you take the reciprocal (flip it)

x^½

√x

x^¾

⁴√x³

Formula for total interest earned

Interest = final amount - initial amount

Formula for compound interest

final amount = initial amount × (1+ (interest rate/100)) ^no of years

How are bound ranges shown as

0.5 ≤ x ≤ 1.5

What do you plot on a cumulative frequency graph?

the upper class boundary (the bigger number)

How do you find the median on a cumulative frequency graph?

find the highest cumulative frequency and divide it by two. read across from the y-axis to convert it on the x-axis

How do you find the upper quartile of a cumulative frequency graph?

¾ × highest cumulative frequency

then convert it

How do you find the lower quartile of a cumulative frequency graph?

¼ × highest cumulative frequency

then convert it

How do you find the interquartile range?

Upper quartile - Lower quartile

What is the formula for frequency density?

frequency/class width

How do you find the mean of a frequency table?

1. Find the midpoint of each value

2. Multiply each frequency by its midpoint

3. Find the total m×f

4. Divide by the total frequency

How do you find the median of a frequency table?

1. Add up all the frequencies together

2. Find the middle position (n+1/2)

3. Work through the cumulative frequencies until you reach that number

4. Find the midpoint of the range of numbers

Probability of independent events (probability of getting A and B)

P(A and B) = P(A) × P(B)

Probability of mutually exclusive events (probability of getting A or B)

P(A or B) = P(A) + P(B)

what is sin(x) equal to

sin(x) = sin(180-x)

Formula for the sine rule

Sin(A)/a = Sin(B)/b or a/sin(A) = b/sin(B)

What do the capital letters represent?

The angle

What do the lower case letters represent?

the sides

When is the sine rule used?

when you either have:

-two angles and one side or

-two sides and one angle

When is the cosine rule used?

When you either have:

-three sides given and want to find an angle

-Have two sides and an angle given between them (like a sandwich)

What is the cosine formula to find a side?

a²=b² + c²-2bc×cos(A)

What is the cosine formula to find an angle?

Cos(A) = b²+c²-a²/2bc

How do you find the area of a non-right angled triangle?

Area = ½ab sin(c)

a and b are the sides given

c is the angle given

What is the relationship between A and a?

A is the angle and a is the side opposite A

What are vectors?

they have magnitude (size) and direction

What does the top number mean in column vectors?

+ is right

- is left

What does the bottom number mean in column vectors?

+ means up

- means down

How do you find the vectors between two points?

A = (x₁, y₁)

B = (x₂, y₂)

AB→=(x₂-x₁/y₂, y₁)

How do you find the length of a vector?

√a²+b² (a/b)

Parallel vectors

two vectors are parallel is one is a multiple of the other

what does AB→ mean

it means the vector from point A to B. it shows the direction and represents the movement needed to get from the first point to the second

Vector addition

a→ + b→means go along vector a then go along vector b

- it means follow the direction

Vector subtraction

a→-d→ means go along vector a then go backwards along vector d

-it means to travel in the opposite direction that is shown

Vectors on a straight line

points are on a straight line if they have parallel vectors and have a point in common

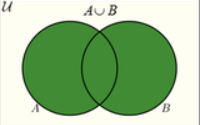
A∩B

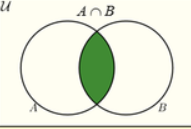
A∪B

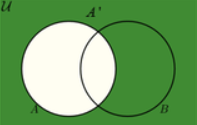
A'

A∩B’

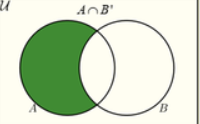
A’∩B

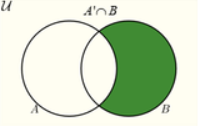
A∪B’

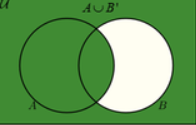
A’∪B

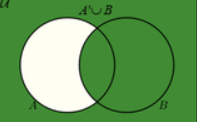
A’∪B’

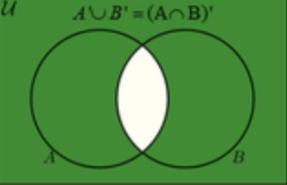
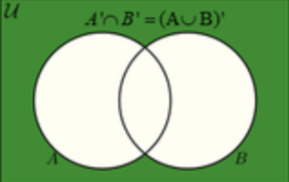
A’∩B’

Direct proportion

y = kx

Inverse proportion

y = k/x

What are the roots in a quadratic graph?

The two points where the line crosses the x-axis

How do you find the roots of a quadratic graph?

by factorising, using the formula or CTS

What is the turning point of a quadratic graph?

Where the graph changes direction (it is the maximum/minimum)

How do you find the turning point of a graph?

x-coordinate is:

x = -b/2a

Then substitute x back into the y=ax² + bx + c formula

How do you find the y-intercept of a quadratic graph?

subsitute x=0

y=ax^2 + bx + c

How do you solve a quadratic inequality?

1. Solve the related equation and find x (the roots) (0= ax^2 + bx + c)

2. Work out where the equality is true

-if it is >0 we want the parts above the x-axis and outside the root (x>? and x

What is the formula for a U-shaped parabola

y= ax^2 + bx + c

(positive coefficient)

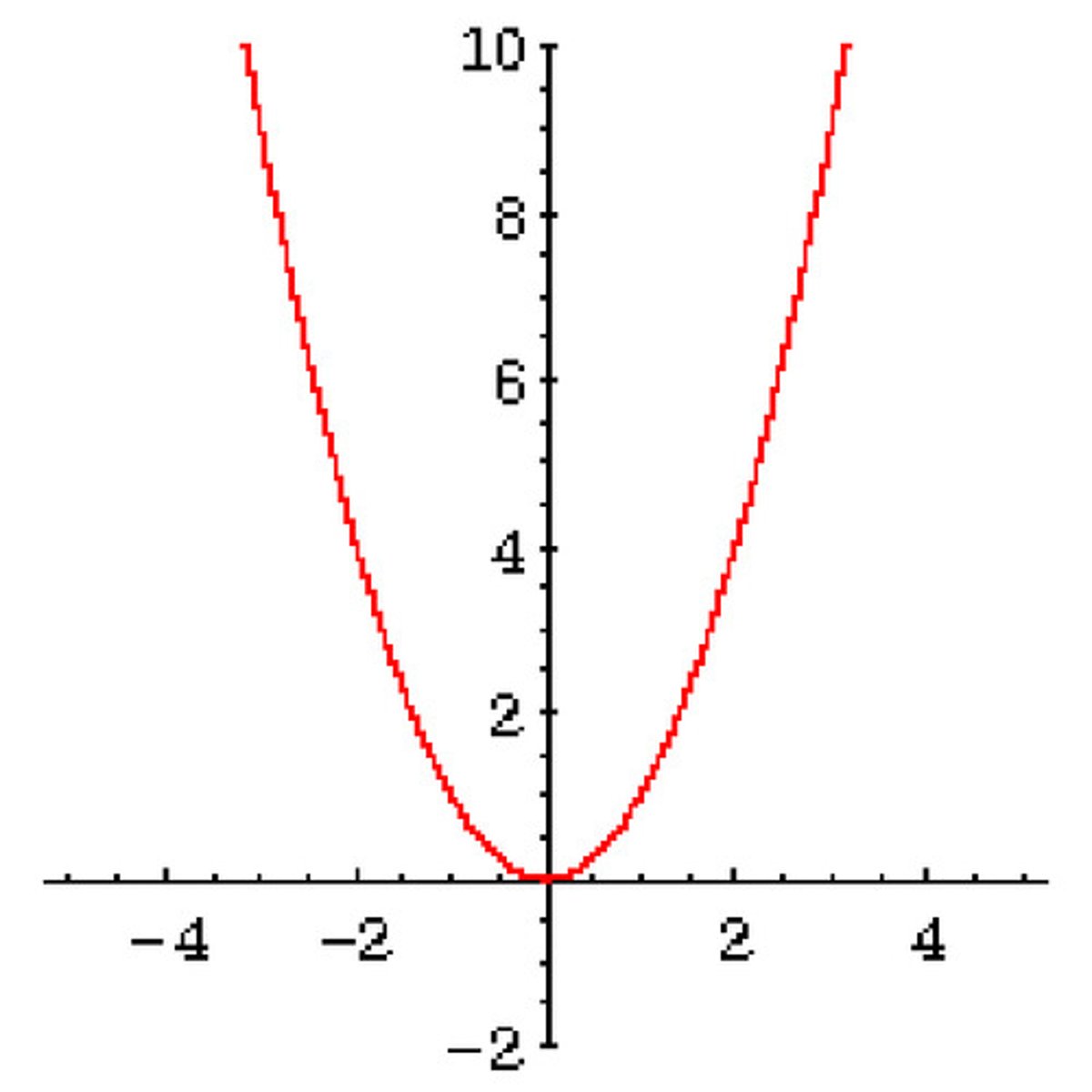
What is the formula for a ∩-shaped parabola

y= -ax^2 + bx + c

(negative coefficient)

How do you factorise when the coefficient isn't 1?

ax^2 + bx + c

-Find two numbers that multiply to ac

-and add to b

When can you add or subtract surds?

when the base numbers are the same

How would you rationalise 1/√3?

1/√3 × √3/√3 = √3/3

How would you rationalise 5/2√7?

5/2√7 × √7/√7 = 5√7/2×7 = 5√7/14

How would you rationalise 3/5 - √2

multiply with oposite signs

3/5 - √2 × 5 + √2/5 + √2

How do you complete the square?

1. half the coefficient of x (the number infront of x)

2. Rewrite the equation in the form of (x+a)^2 + b. a should be half the coefficient

3. minus the half coefficient squared

What do parallel lines have in common?

They have the same gradient

How do you find the equation of a line that is parallel to another line and passes through a point?

1. Substitute the gradient in because parallel lines have the same gradient

2. Substitute the point in to find the y-intercept. E.g if the point is (1,4) the new equation would be 4 = m1

3. re-write in the form of y = mx + c

what does the equation y = mx + c mean?

Y - Represents the vertical coordinate of any point on the line.

X - Represents the horizontal coordinate of any point on the line.

M: Represents the gradient,

C - Represents the y-intercept.

what does a mean in the equation y=ax^2+bx+c?

- if it is positive, the line is a U shape

-if it is negative, the line is a n shape

-if the magnitude is bigger, the line is narrower

-if it is smaller, the line is wider

-if it is zero, the line is straight

How do you find the line of symmetry for a parabola?

the x coordinate is x = -b/2a

substitute x value into the equation y=ax² + bx + c

How do you find if lines are perpendicular?

they have gradients that multiply to -1

• m₁ × m₂ = -1

• m₂ = -(1/m₁)

How do you find the midpoint of two given points?

find the average of the x and y coordinates

How are vertical lines shown

x=a

How are horizontal lines shown

y=a

How do you calculate the gradient?

y₂-y₁/x₂-y₁

How do you calculate the distance between two points?

√(x₂-x₁)² ₊ (y₂-y₁)²

What are the 4 types of transformations?

Translation

Reflection

Rotation

enlargment

translation

to move a shape

What does the top number mean in translations

right for a positive number and left for a negative number

What does the bottom number mean in translations

up for a positive number, down for a negative number

Formula for the area of a sector of a circle

Sector area = (angle/360) × πr²

Formula for the perimeter of a sector of a circle

Sector perimeter = arc length + 2r

Formula for the area of an arc of a sector

Arc area = (angle/360) × πd

Formula for the length of an arc of a sector

Arc length = (angle/360) × 2πr

Formula for the volume of a sphere

Volume = 4/3 × πr³

Formula for volume of a cone

Volume = πr² × h/3

formula for the curved surface area of a cone

Curved surface area = πrl

What is 'h' in cones

verticle height

What is 'l' in cones

slanted height

Formula for the total surface area of a cone

Total SA = πrl + πr²

The angle in a semicircle is a right angle

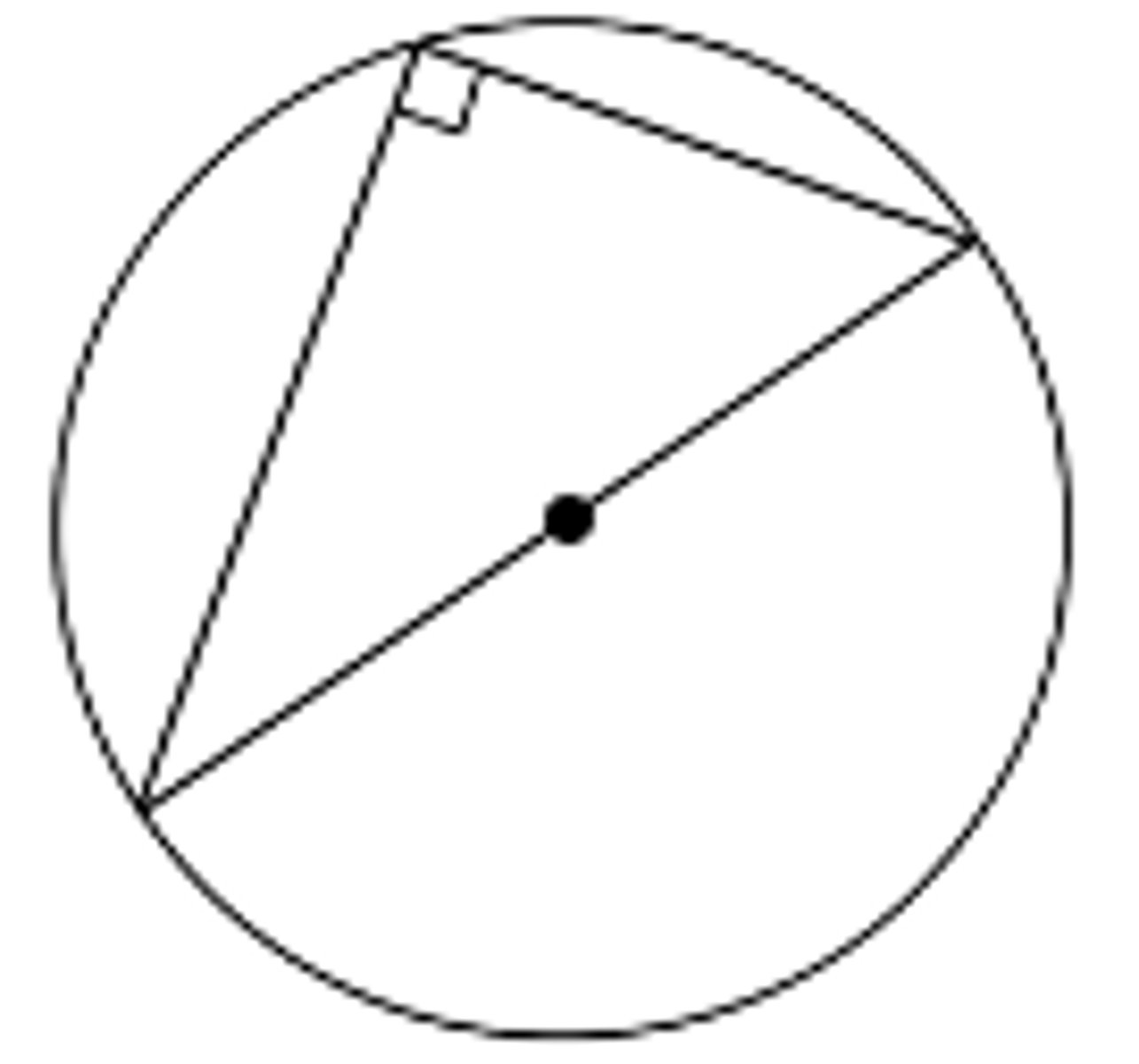
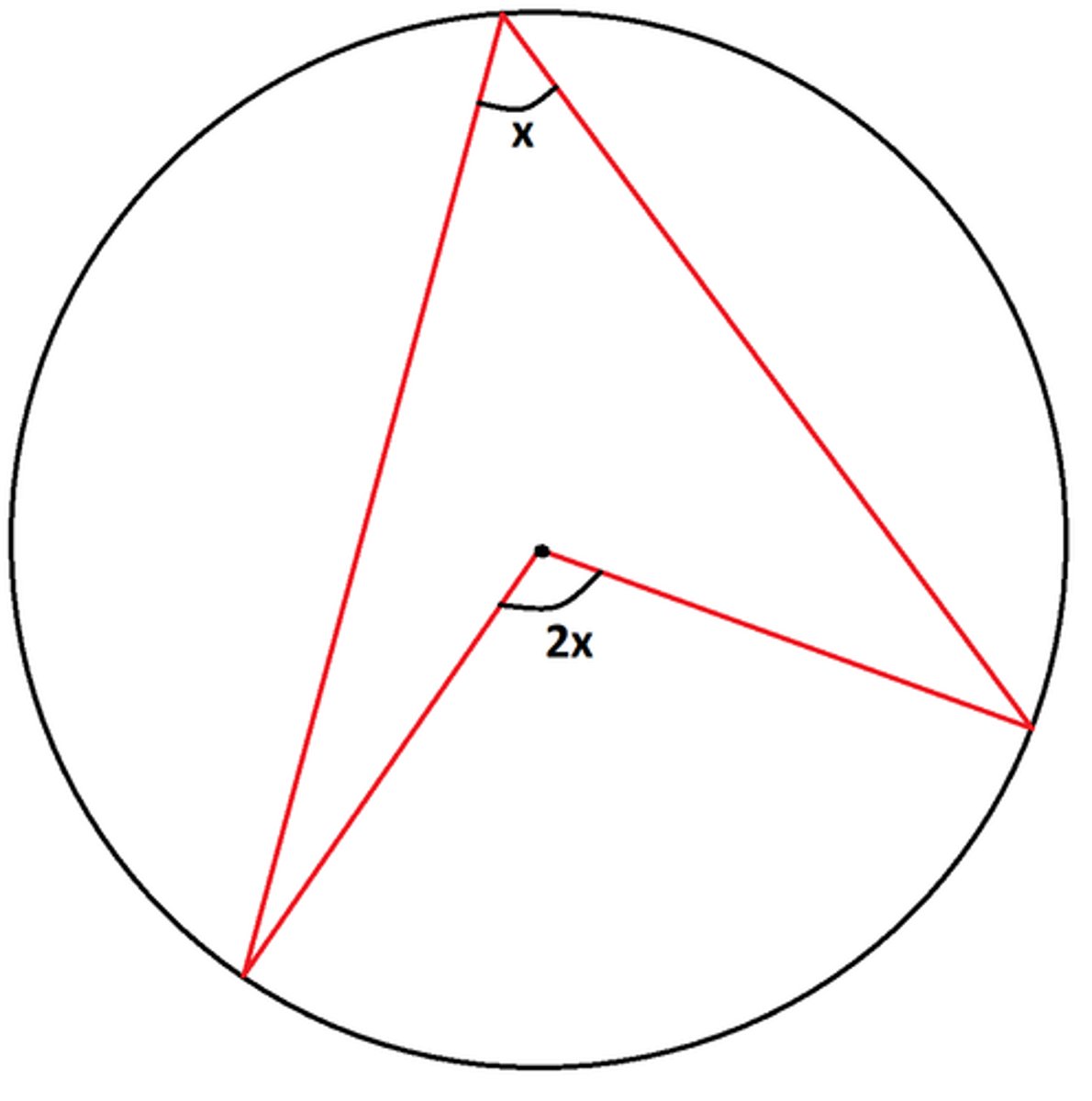
The angle at the centre is twice the angle at the circumference

(angles must be facing the same way)

Formula for the surface area of a sphere

SA = 4πr²

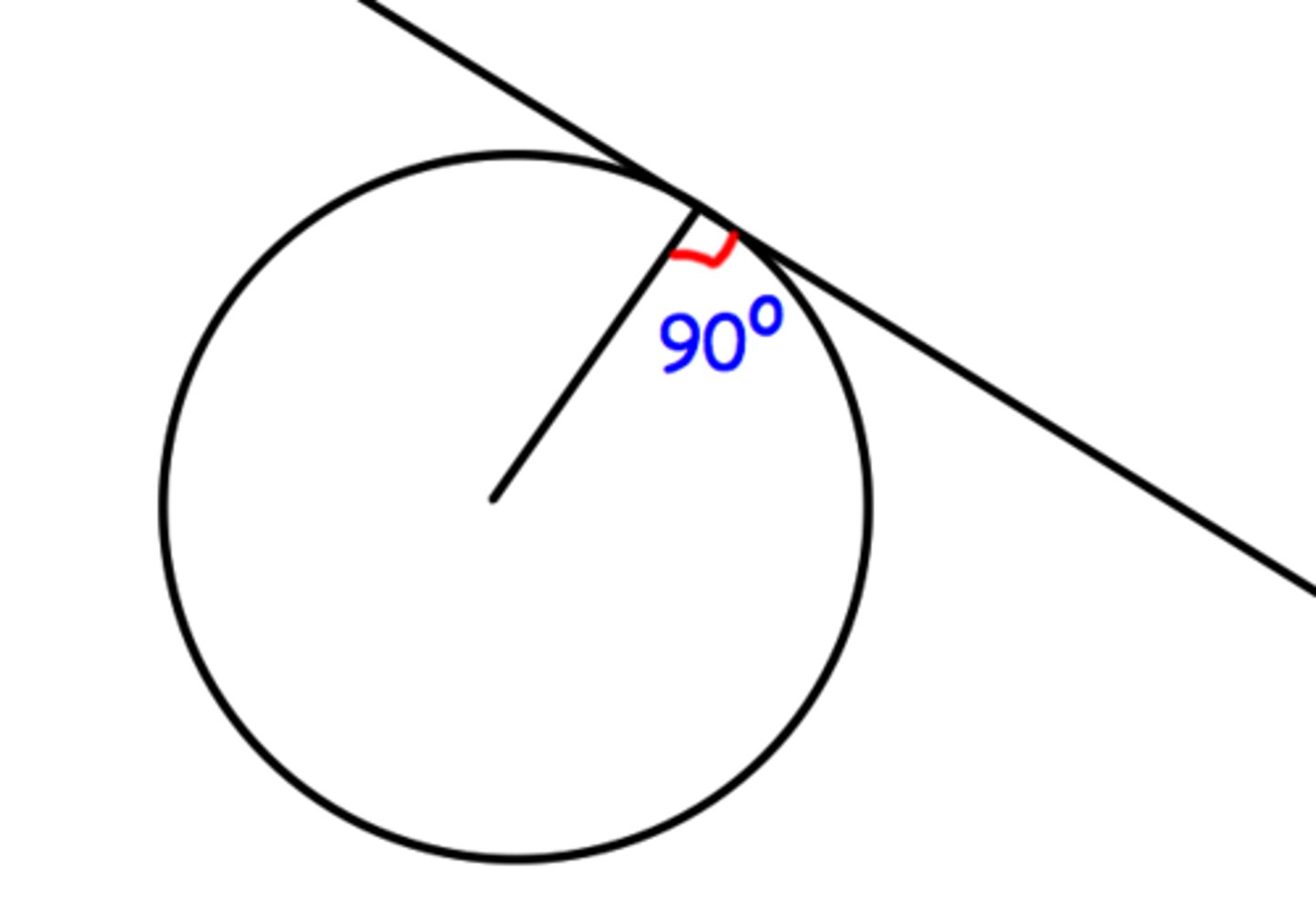
Radius meets tangent at 90 degrees

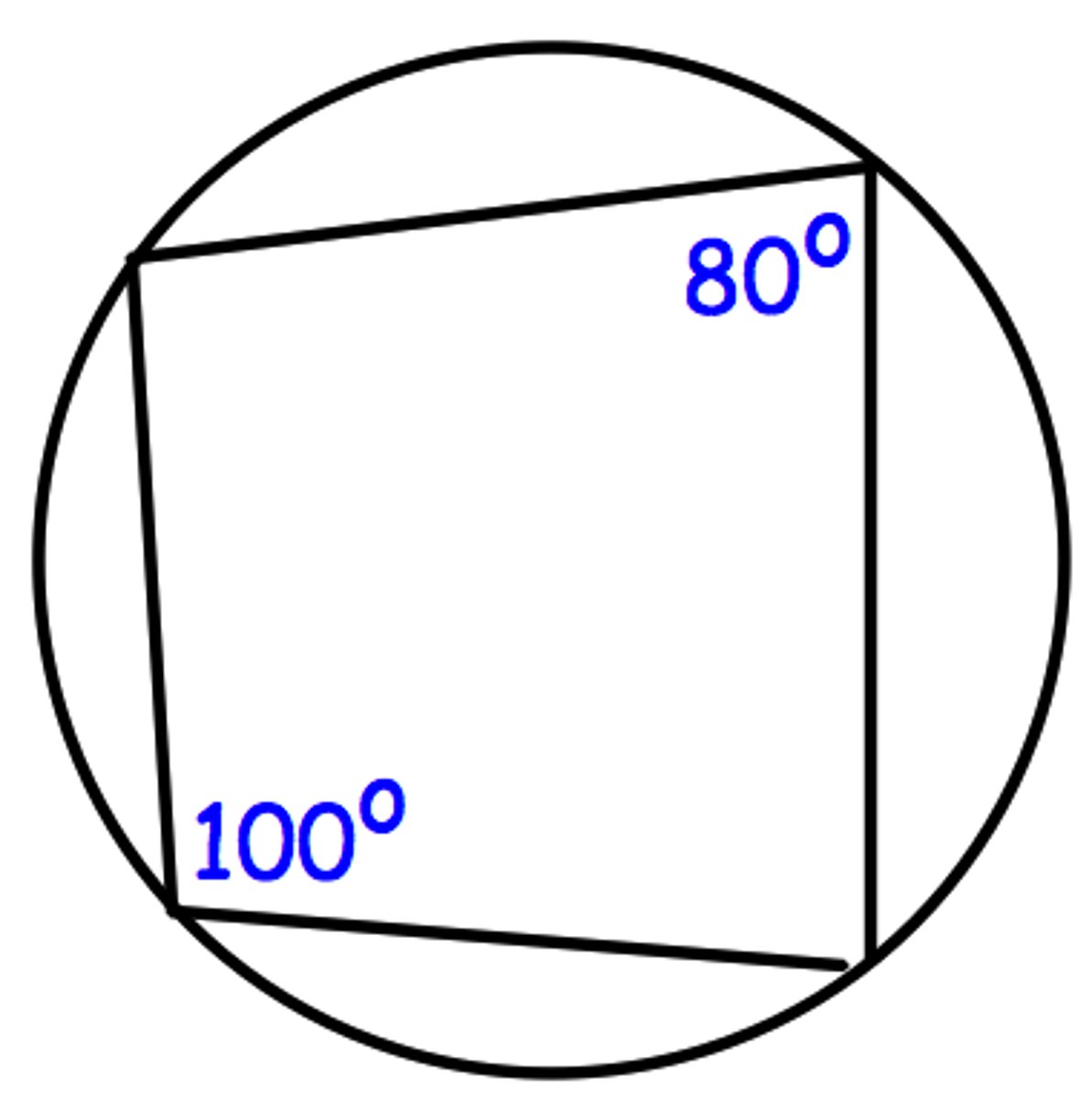
Opposite angles in a cyclic quadrilateral add up to 180°

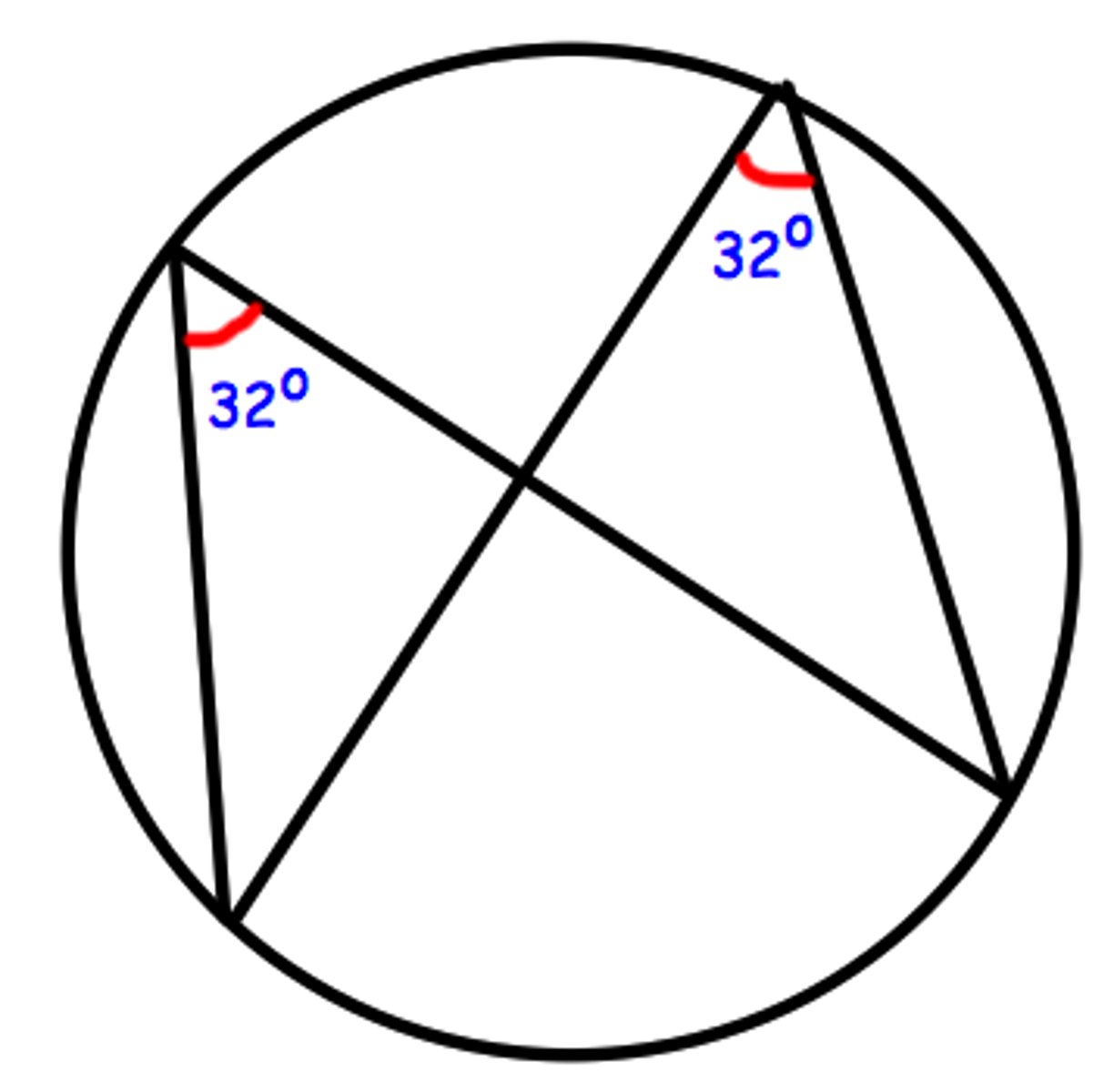
Angles in the same segment are equal

Tangents to the circle from the same point are equal in length

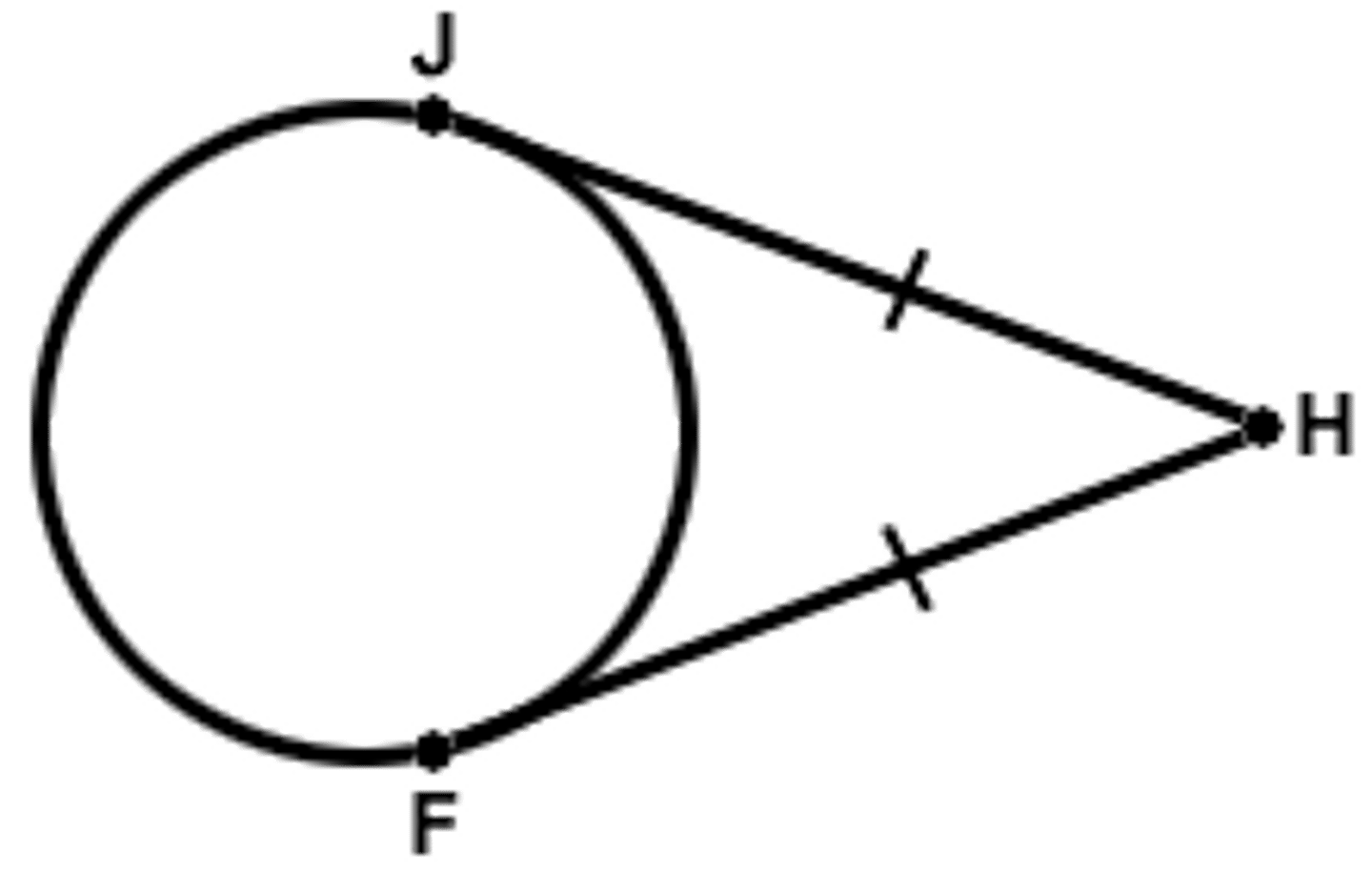
-Alternate segment theorem

-The angle between the tangent and the side of the triangle is equal to the opposite interior angle

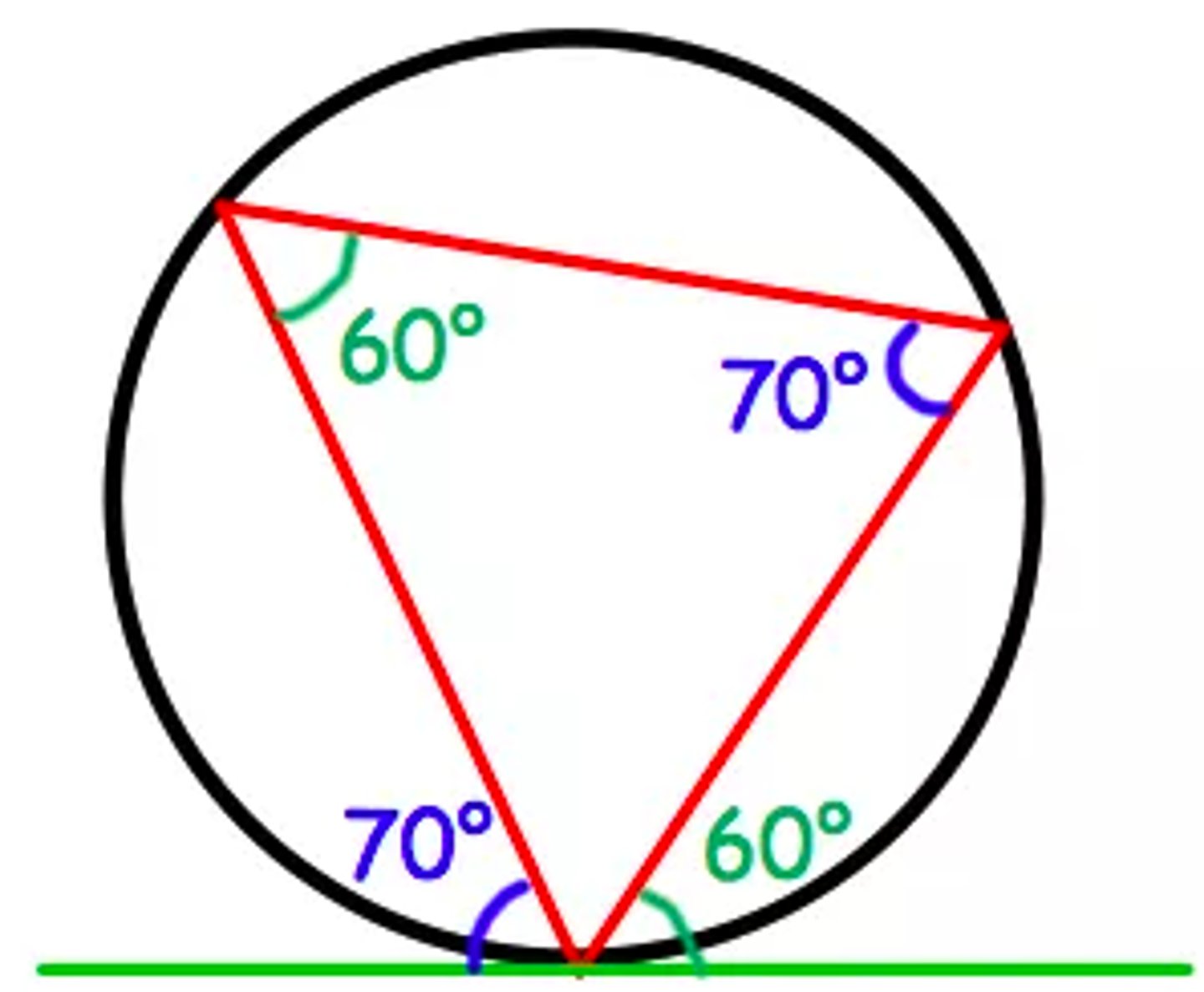
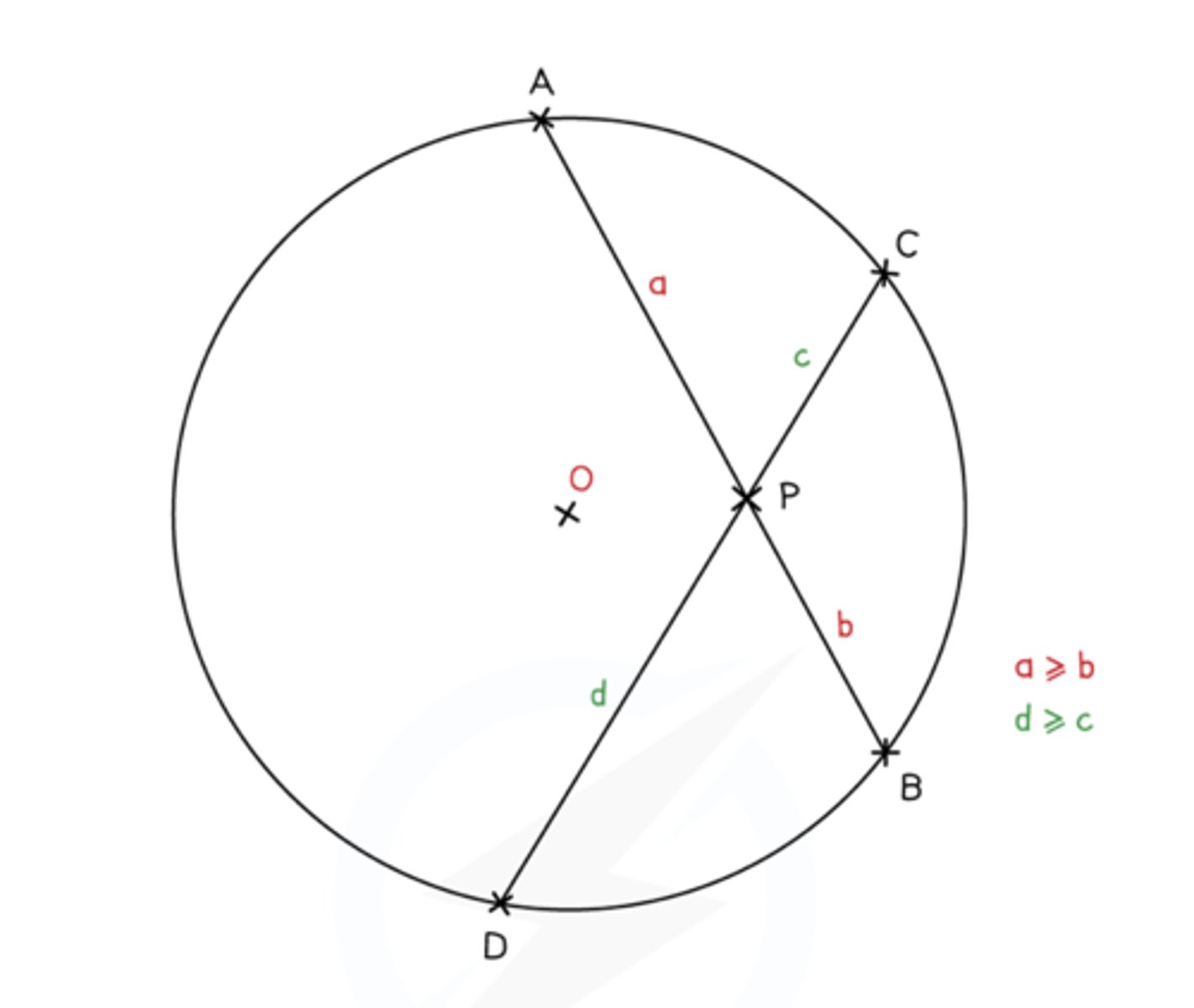
-intersecting chord theorem

-If two chords intersect inside a circle, then the product of the segments from one chord is equal to the product of the segments from the other chord

a×b = c×d