Sorting Algorithms

Bubble Sort

A simple comparison-based algorithm where adjacent elements are compared, and they are swapped if they are in the wrong order. This process repeats until the array is sorted.

Insertion Sort

A comparison-based algorithm that builds the sorted array one item at a time by inserting each new element into its correct position in the sorted part.

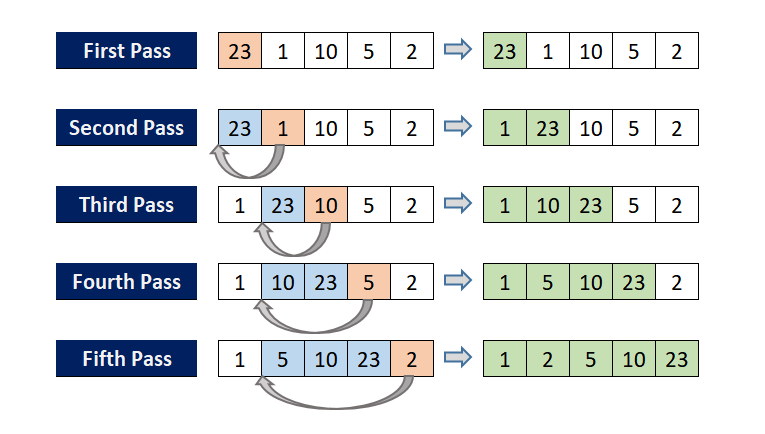
Selection Sort

A comparison-based algorithm that repeatedly selects the smallest (or largest) element from the unsorted portion and swaps it with the first unsorted element.

Quick Sort

A divide-and-conquer algorithm that selects a pivot element, partitions the array into two parts based on the pivot, and recursively sorts the sub-arrays.

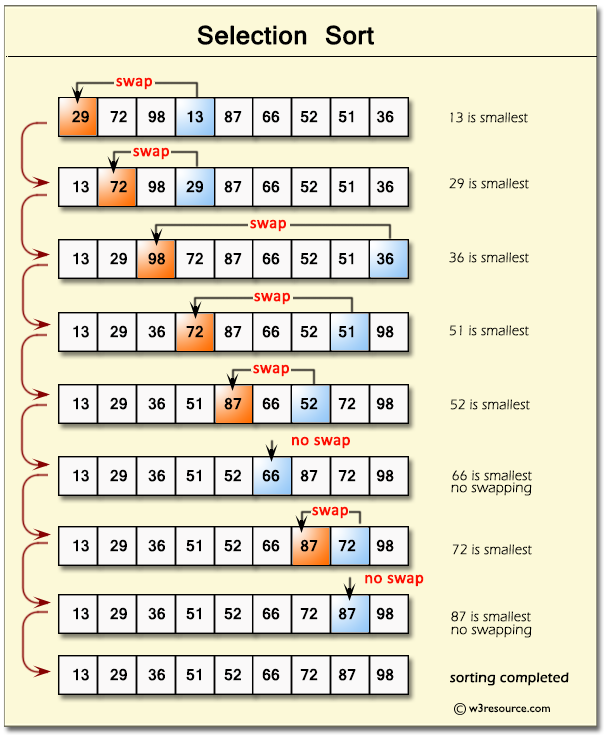
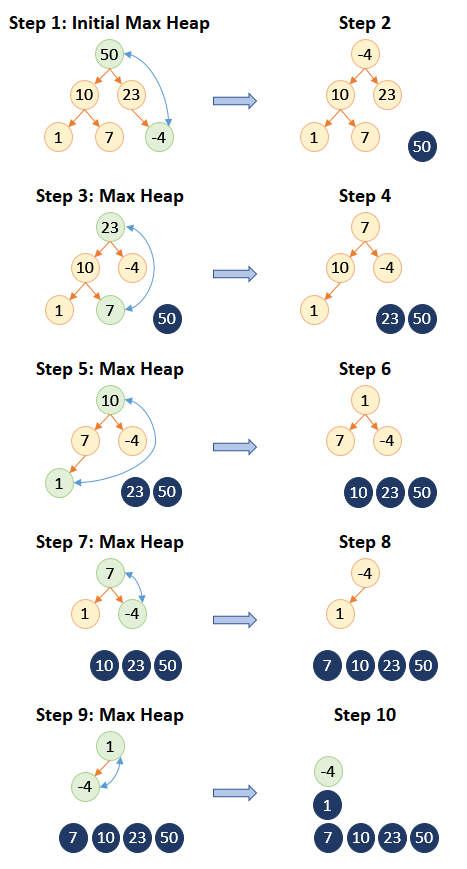
Heap Sort

A comparison-based algorithm that builds a binary max-heap (or min-heap) and repeatedly extracts the maximum (or minimum) element to sort the array.

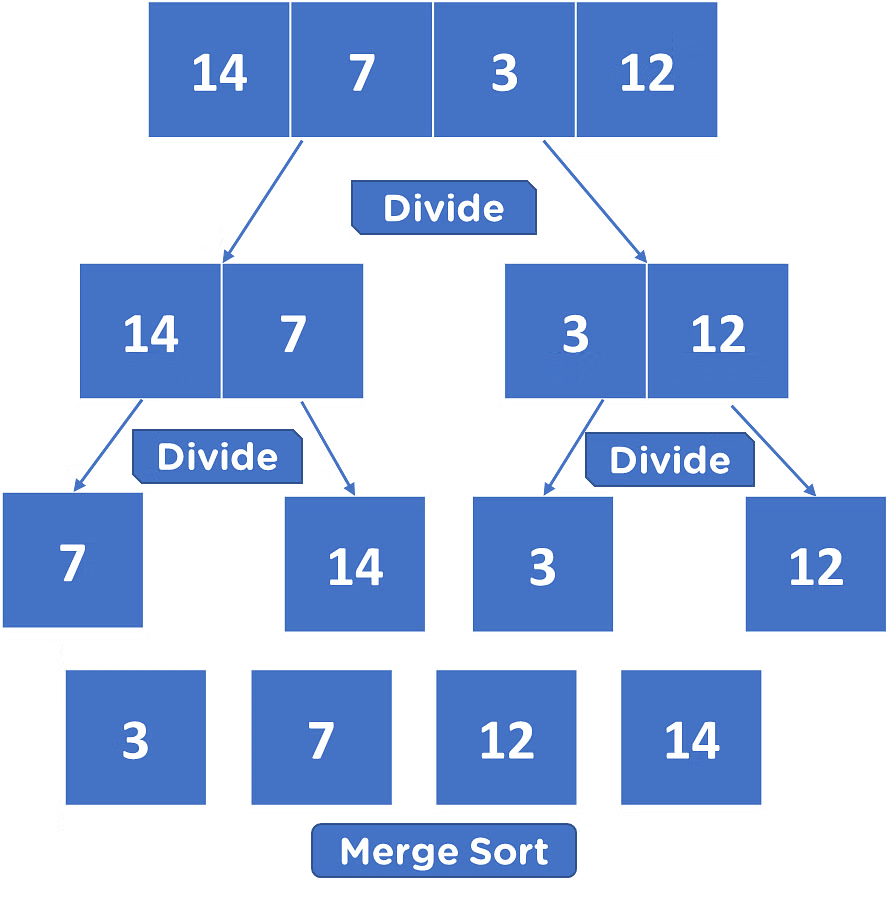
Merge Sort

A stable, divide-and-conquer algorithm that splits the array into halves, recursively sorts the halves, and then merges them back together.

Timsort

A hybrid sorting algorithm used in Python and Java, based on merge sort and insertion sort. It is designed to perform well on real-world data and take advantage of existing order in the data.

Counting Sort

A non-comparison-based algorithm that counts the number of occurrences of each unique element. It works by calculating the position of each element in the output array using the counts.

Bucket Sort

A non-comparison-based algorithm that divides the array into a number of buckets, distributes the elements into these buckets, and then sorts each bucket individually, often using another sorting algorithm.

Radix Sort

A non-comparison-based algorithm that sorts numbers by processing individual digits, starting from the least significant to the most significant digit, using a stable sorting algorithm for sorting digits.

Shell Sort

A comparison-based algorithm that sorts elements far apart (using a gap sequence) before reducing the gap and refining the sorting. It is an optimized version of insertion sort.

What is a stable sorting algorithm?

A stable sorting algorithm maintains the relative order of records with equal keys. For example, if two elements have the same value, their original order in the input array is preserved in the output.

Which sorting algorithms are stable?

Merge sort, insertion sort, counting sort, radix sort, and Timsort are examples of stable sorting algorithms.

Which sorting algorithms are not stable?

Quick sort, heap sort, selection sort, and shell sort are examples of unstable sorting algorithms.

What is an in-place sorting algorithm?

An in-place sorting algorithm sorts the array by modifying the input directly without needing extra space for another array or significant additional memory.

Which sorting algorithms are in-place?

Quick sort, heap sort, insertion sort, bubble sort, and selection sort are examples of in-place sorting algorithms.

What is the main advantage of quick sort?

Quick sort is very efficient for large datasets and has good average-case performance. It often outperforms other sorting algorithms in practice, even though its worst-case performance is not optimal.

What is the key difference between merge sort and quick sort?

Merge sort is a stable algorithm and requires extra space for merging, while quick sort is an in-place algorithm but can be unstable. Merge sort divides the array into two equal halves, while quick sort selects a pivot and partitions the array based on that pivot.

When is counting sort a good choice?

Counting sort is efficient when the range of input values is not significantly larger than the number of elements to be sorted. It works well when sorting integers or small-range discrete values.

How does radix sort work?

Radix sort sorts numbers digit by digit, starting from the least significant digit to the most significant, using a stable sorting algorithm like counting sort at each digit level.

Why is Timsort used in real-world applications like Python?

Timsort is optimized for real-world data. It combines merge sort and insertion sort and takes advantage of existing order within the data, making it perform very well on practical datasets.

What makes heap sort different from other sorting algorithms?

Heap sort uses a binary heap data structure to find the maximum (or minimum) element efficiently. It builds a heap and repeatedly extracts the largest element, rearranging the heap after each extraction.