Motion in Gravitational Fields

gravitational forces involve…

Central body – a object in space where other objects orbit around it (opposite of a satellite)

Mass – a measure of inertia (N1L, an object’s tendency to resist a change in motion)

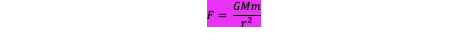
Where

Note: when a constant is used, all units must be SI!!!

• F = the gravitational force (N)

• G = the gravitational constant (6.67x10-11 Nm2kg-2)

• M = the mass of the planet (kg)

• m = the mass of the object (kg)

• r = the distance between the centre of each object, assuming both are spheres (m)

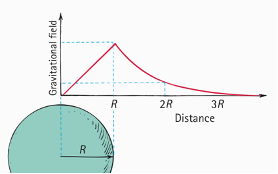
calculate gravitational field strength (acceleration due to gravity)

mg = GMm/r²

g=GM/r² —> does not depend on mass of object, but of central body instead

in m/s/s or N/kg

how gravitational field strength changes with distance

for circular orbits

( - gravitational force

- centripetal force

- centripetal acceleration)

UCM performed with gravity being the provider

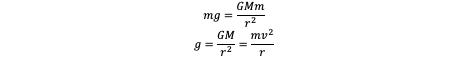
The object will accelerate towards the earth but does not fall to the ground because:

• The object has a tangential velocity (it travels fast enough not to fall into the planet)

• Acceleration towards the ground keeps it in uniform circular motion)

how velocity influence trajectory of projectile

• v < vorbital —> projectile will fall down and hit hearth

• v = vorbital —> go into orbit

• v > vorbital —> elliptical orbit

• v > vescape —> moves away from planet and escapes gravitational field

mass in orbital eqs

Mass does not affect the orbital velocity of a satellite since it is not in the equations

→ Weightlessness (we somewhat explored this in the non-uniform circular motion section)

→ Occurs when apparent weight is zero

∴ when you are in freefall (only force is gravity and there is no reaction force)

astronauts in space are in freefall (only experience gravity), feel no normal/reaction force, so they feel weightless

orbital radius vs altitude

Radius - The distance from the centre of the central body to the centre of the satellite

Altitude - height above the surface of the planet

We want the radius when doing calculations, not the altitude:

Altitude = total radius – radius of central body

orbital velocity

Since a satellites centripetal force is equal to the gravitational force,

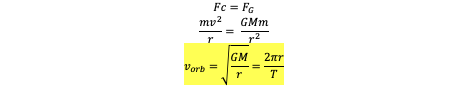
Note: if a heavier satellite was placed in the same orbit as a lighter satellite, orbital velocities of both would be the same, since the mass of the satellite has no effect on orbital velocity

→ same orbit = same velocity = same acceleration

how to calculate orbital period

use K3L

Orbital period is NOT affected by the mass of the satellite, but by other factors

According to K3L:

T²/r³ =(4π²2)/GM

T2=(4π²r³)/GM

When radius increases, period increases

When the mass of the central body increases, the period decreases

define Satellite + types

an object that moves around a larger object

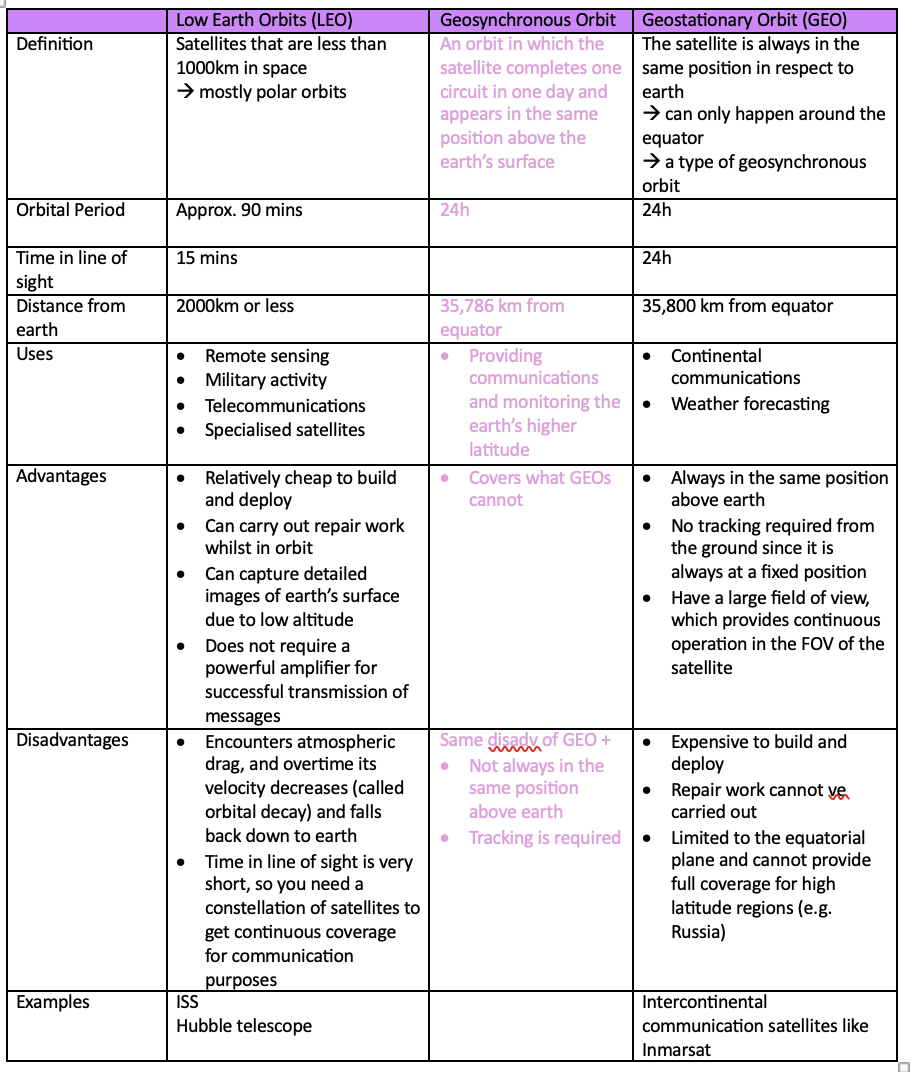
• LEO = low earth orbit (period is way faster than 24h)

• GEO = geo stationary orbit (period is 24h, velocity relative to earth is 0, on equator)

• geo synchronous = period is 24H but it has an elliptical orbit and is not around the equator

compare LEO and GEO

how to calculate velocity

use v=√GM/r

or use K3L to find T/r, substitute it in for v=2r pi / T

escape velocity

minimum velocity needed at a given distance from the planet to escape from the gravitational field of that planet

—> when e total is positive, so K is way bigger than U

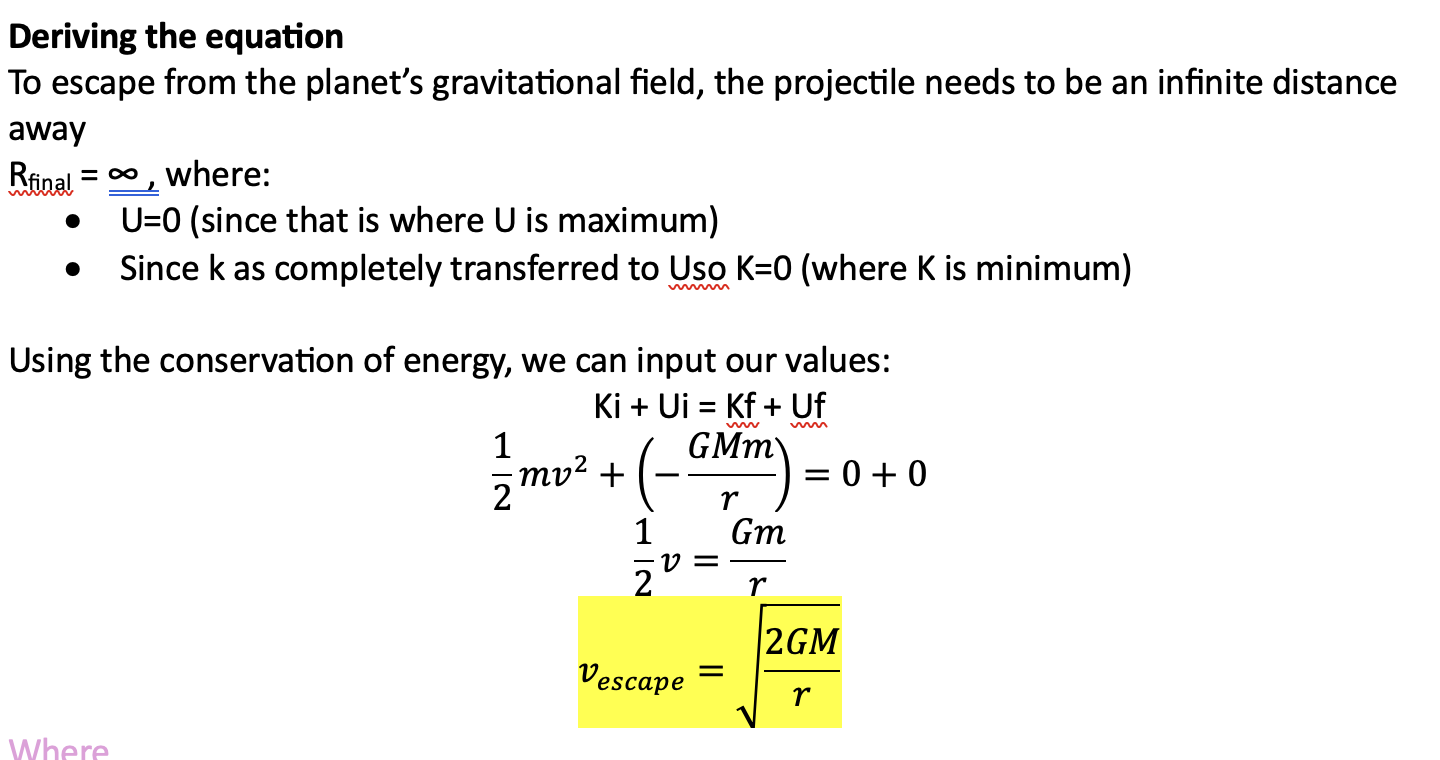
gravitational potential energy

potential an object has to do work due to it being at a point in a gravitational field

U=mgh is for low to the ground, but once you get higher you need a different eq to account for changing gravitational field strength

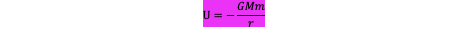
When u=0 r= infinity (infinity is a point, and r moves back from that)

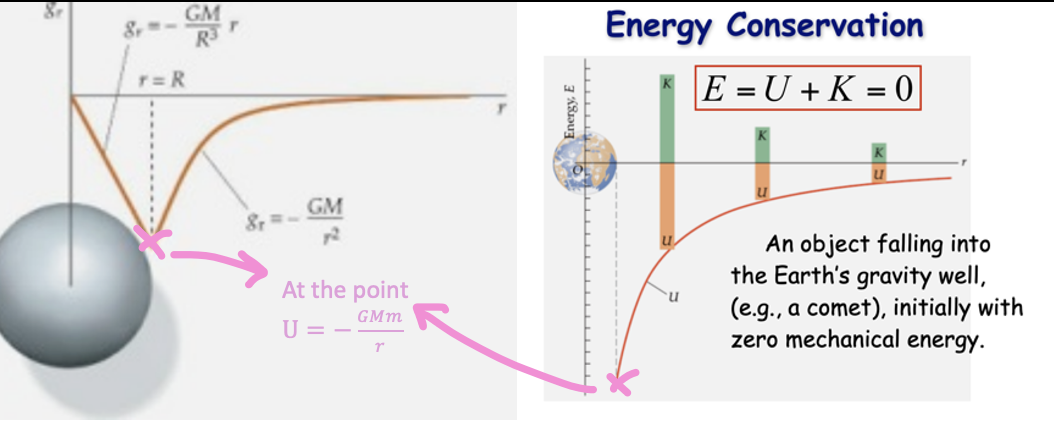
total energy of a satellite

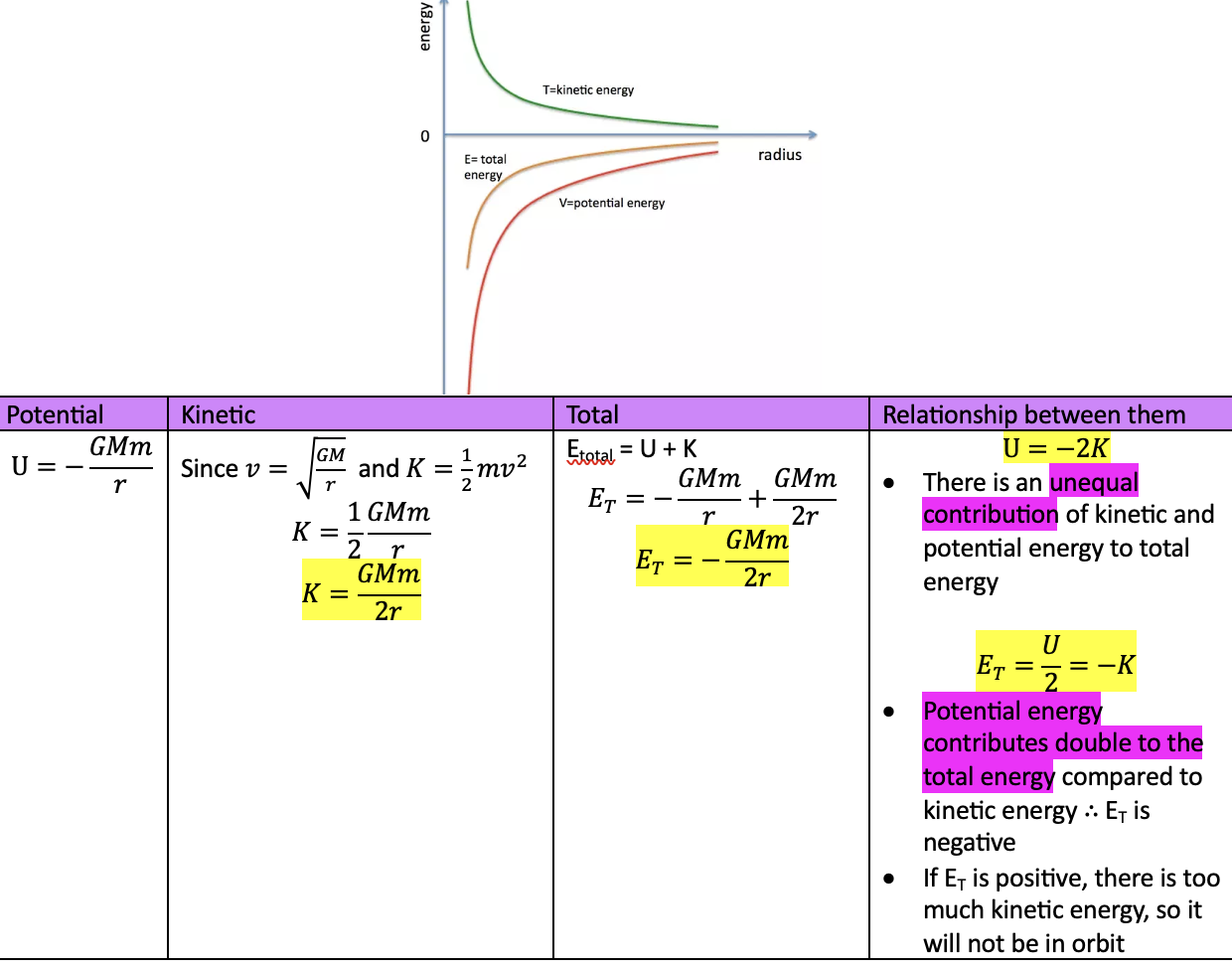
calculating work

can utilise the earth’s rotation to give an extra speed boost to the rocket (launch on equator since it has fastest linear velocity)

work to change orbits

THIS ENERGY DOES NOT GO IN TO CHANGE THE VELOCITY REQURIED TO STAY AT THAT ORBIT → e.g. changing to outer orbit = k still decreases and U increases despite adding K energy to move it (only goes into moving motion)

• moving further away from central body

  • More velocity by putting thrusters in same direction as velocity = more KE = moves out because gravity to weak

  • moves to an elliptical orbit —> when v= √(GM/r), it is in UCM, and since V > Vucm it moves to elipse

  • need to speed up at apoapsis to turn back to UCM

  • The central body will be at the focus closest to where you speed up

• Moving to an orbit closer to the central body

  • Less velocity by putting thrusters in opposite direction to velocity = less KE = it gets pulled in because gravity too strong

  • elliptical orbit

  • need to slow down at periapsis to turn back to UCM

  • The central body will be at the focus furthest away from where you slowed down

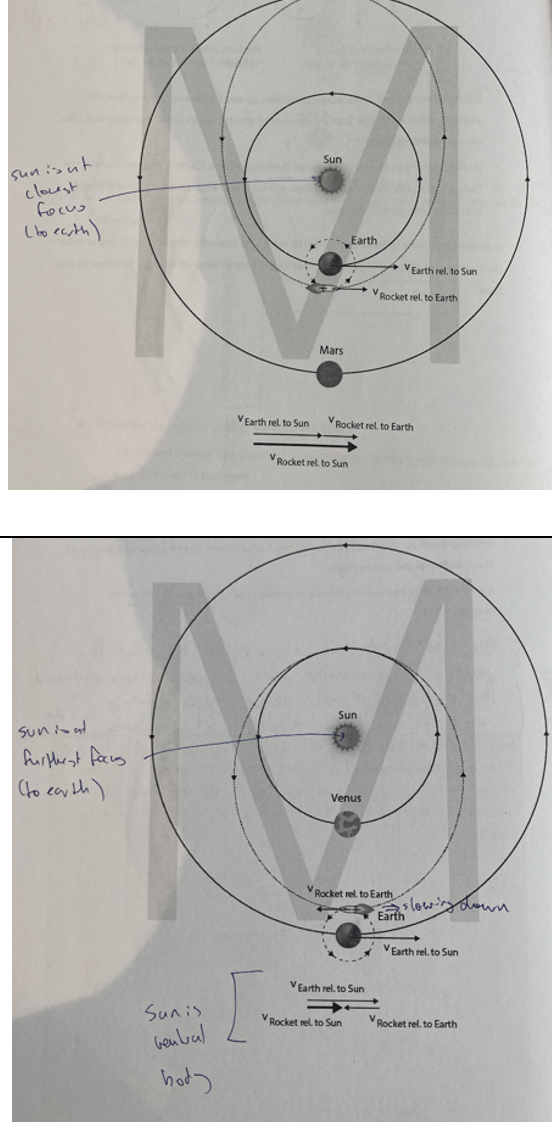
moving to different planets

• outer planets

  • Moving out = speed up when at the fastest point at earth and sun

  • Sun is at the focus closer to the original position of earth and the spacecraft

• inner planets

  • Moving in = slow down when at slowest point at earth and sun

  • Sun is at the focus further away to the original position of earth and the spacecraft

keplers laws apply to what kind of orbits

ellipitcal —> most orbits are elipses

Since a circle is a type of ellipse, you can use these elliptical equations for circle orbits as well BUT YOU CANNOT USE CIRCULAR EQUATIONS OR ELIPSES

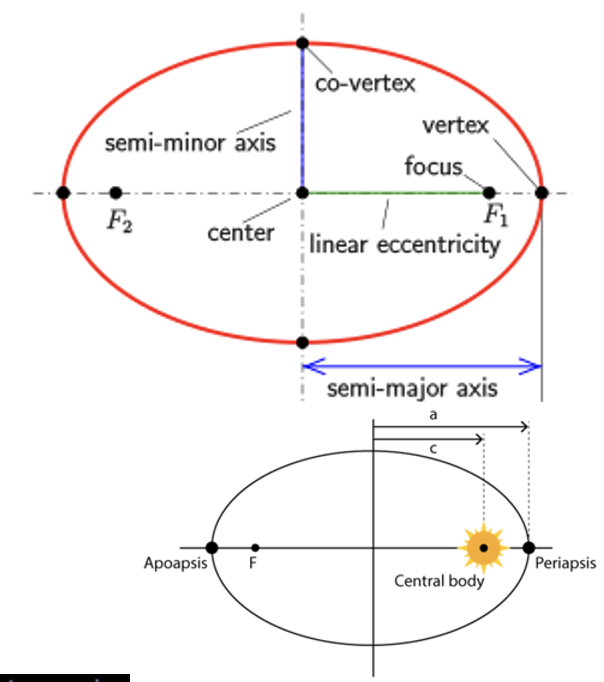
K1L

Planets move in elliptical orbits with the Sun as a focus

• apo = further away from central body

• peri = closer to central body

Eccentricity – how flat the ellipse is e.g. Large eccentricity = Halley’s comment e.g. Low eccentricity = Earth	e = c/a
Semi-major axis - average distance from the central body	a
Semi-minor axis	b
distance to focus	c
distance to periapsis	= a - c
distance to apoapsis	= a + c
average radius	distance to apo + distance to peri ÷2

K2L

A planet covers the same area of space in the same amount of time no matter where it is in its orbit

• we can relate speeds at periapsis and apoasis using this law:

  va ra=vp rp

satellite travels faster at periapsis than apoapsis

• using conservation of energy

  • At the periapsis, the satellite is closer to the central body, so it has less gravitational potential energy and more kinetic energy, thus travelling faster

  • At the apoapsis, the satellite has more gravitational energy because it is further away from the central body, so it travels slower

• using k2l

  • As the periapsis is closer to the sun, the satellite can cover a large area very fast (since area = ½ r²𝜃), thus it travels faster around periapsis

  • As apoapsis is further away from the sun, it covers that same area in a slower amount of time ( thus it moves at its slowest at the apoapsis

k3l

note: r = the average distance

in SI units K = 1

if it follows keplers law, the ratio of r³/T² will be the same for all satellites orbiting a central body

different ways to use k3l