3 - equations and inequalities

3 ways of solving simultaneous equation

elimination (the first one we are taught)

substitution (rearrange one then sub it into the other)

set them equal to each other (only if one side of equation is same for both of them)

one of the rules of solving inequalities

when you multiply or divide both sides by a negative the inequality switches around (flips)

how to answer in set notation

always use curly brackets

x: means ‘x is such that’

use a union between them if there is more than one

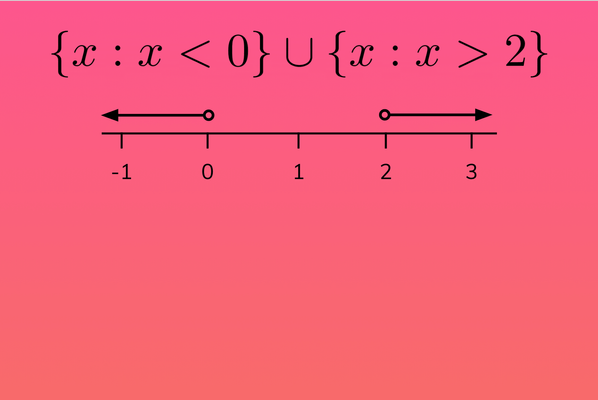
how would you solve a question that looks like this

-5<2x+3<7

still try to get x on its own by doing the same to every part of the equation as you do to the part with x in it

ans = {x: -4<x<2}

how would you solve a question that looks like this

2x<5x+1<3x+7

split it into 2 normal inequalities (2x<5x+1 and 5x+1<3x+7) then solve each one individually to get the range of x answer

ans = {x: 1/3<x<3}

how to solve two separate inequalities

solve them both then sandwich them if possible or make a new inequality that satisfies both

how to solve a quadratic inequality

make it 0 on RHS

solve as usual

draw graph and pick correct side of the y axis to solve inequality

write the range/inequalities

what is always good to write after a ‘show that’ question

‘as required’ when you get to the answer they wanted you to