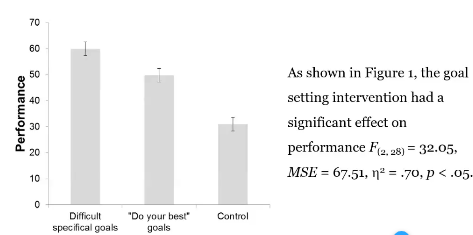
Lecture 6 - One way ANOVA

What does ANOVA mean?

Analysis of variance

What is the flaw of t-tests?

• Limits the number of things that we can measure (2 means) 

• If you do t-tests repretedly, you expose youself to type 1 error

• Restrictions on the number of means

T-tests have two sample means

What is another way of saying all means are equal

No between groups varaibility (this is the null hypothesis)

As f gets larger

More between group variability

• F is asking if you have so much in between group variability that if you picked up a plant out of the pile it probably wouldn’t be the mean

• F has two degrees of freedom

When do you use an one way anova

When there is more than two experimental groups

Why don’t we just use multiple T-Tests

We want to limit type 1 error and if you do t-tests repeatedly, you would expose yourself to those errors 

• You can compute how many you would have to do with k

• As my number of groups go up my number of comparisons go up which can get to be too many comparisons  

• The more comparisons you make, the more chances you have of a type 1 error

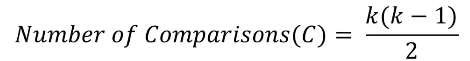
What happens to the alpha when there are many groups

Each test has an alpha (0.05), but when you do many t-tests, your alpha would change - 1/20 but your doing many tests so if there is 20, 1 will have an error

• If i had 6 comparisons and your making them at 0.05 it might be 6.5  

• You will make a type 1 error eventually  

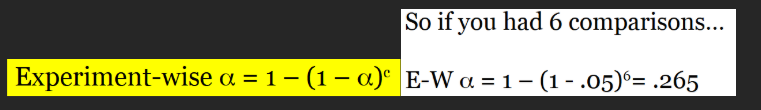
ANOVA Alternative Hypothesis

Not all population means are equal (at least two means are different from each other)

• Doesn’t mean that they are all different

• ANY TWO ARENT EQUAL TO EACHOTHER  

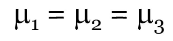
3 Assumptions of a 3-way ANOVA 

(if these conditions are met your ANOVA will be accurate)

1. Observations are normally distributed within each population (bell curve)

2. Variance in each group is equal (homogeneity of variance) → pooled variance

3. Observations are independent (each person is only giving you one observation which is what makes it one way) → if one person is under one condition they arent in the other 

Partitioning Variance

How much of the observed variance in the DV is due to the manipulation (f-statistic)

• What proportion in the DV is due to manipulation and what have percent is leftover'

• breaking down the total amount of variation in a set of data into different sources to see where the differences come from

On average is there more variance due to the music playing or just error variance within a condition

F

What poportion of the variance is due to the thing that we manipulated and what is just error 

What is a source table

Organizing source of variance

Group, error and total df

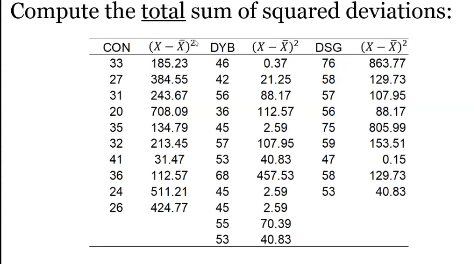
Calqulating ss total

SS total: Grand mean (ignoring groups) - Each score squared 

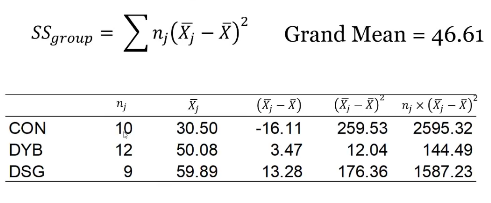
Calqulating group ss, and error ss 

Add totals together 

Error ss: total - group ss

Compute Mean SS

(dont fill last one, this is the overall variance)

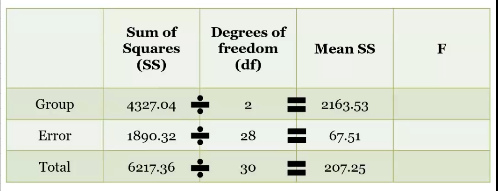
Calcuating F on the table

This is a ration 

• Greater than 1 = more variance due to the group than error 

• Look up f critical (find where df meet) 

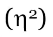
% of variation that can be attributed to the treatment differences (effect size) 

• Easy to calculate but slightly biased 

Example finding report (one way anova) 

*without knowing what means are different for eachother