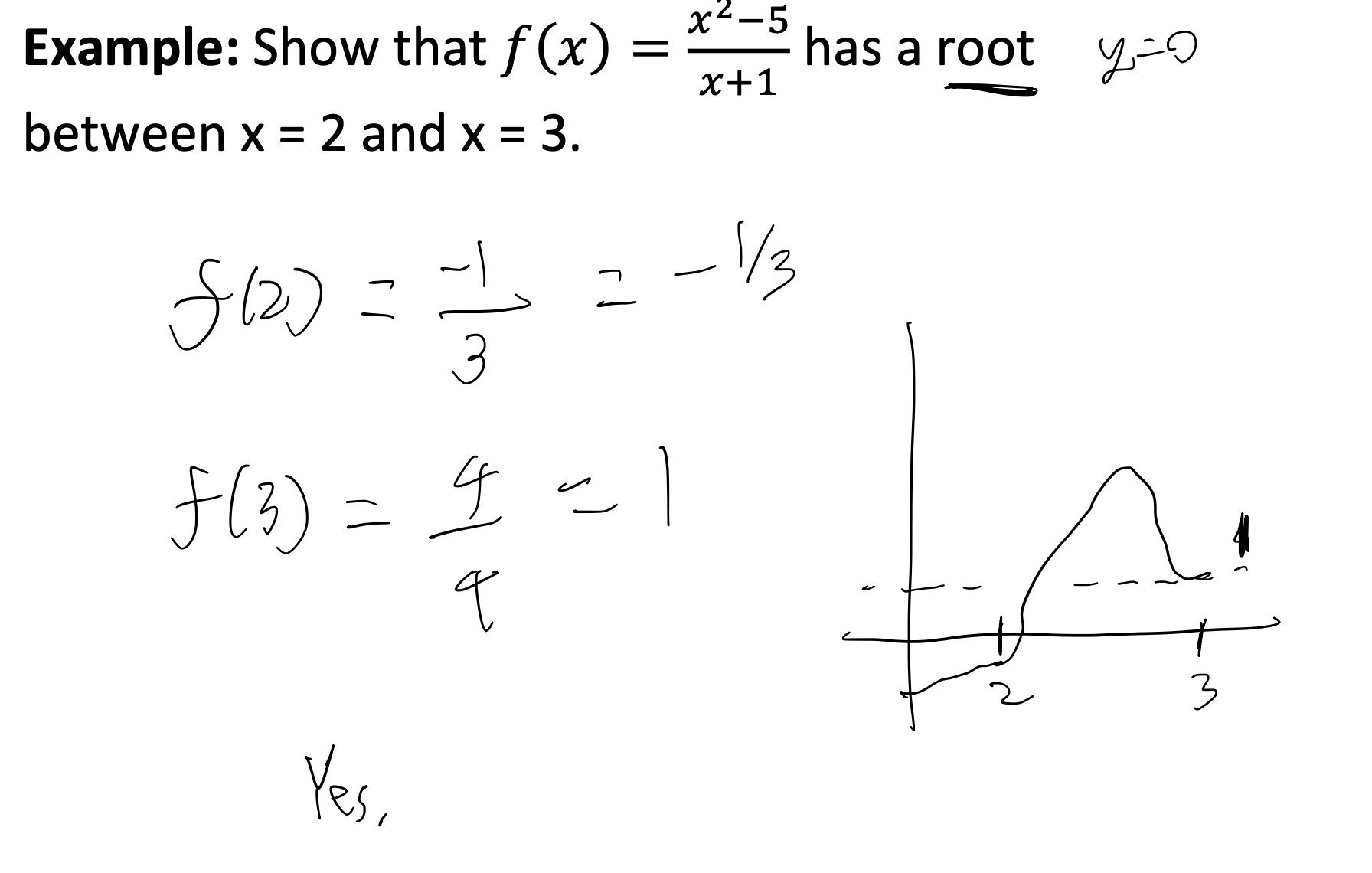Calculus: Limit & Continuity

limits

as f(x) x approaches c, it is equal to L

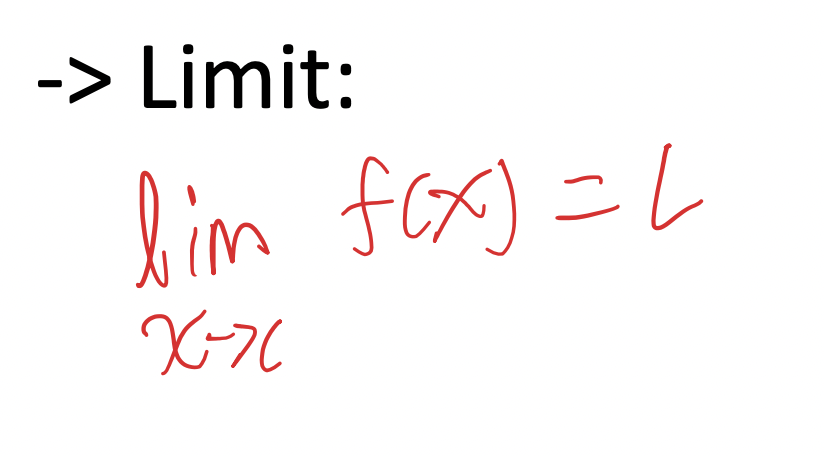
When does limit exist?

Both right and left handside limits are equal to each other.

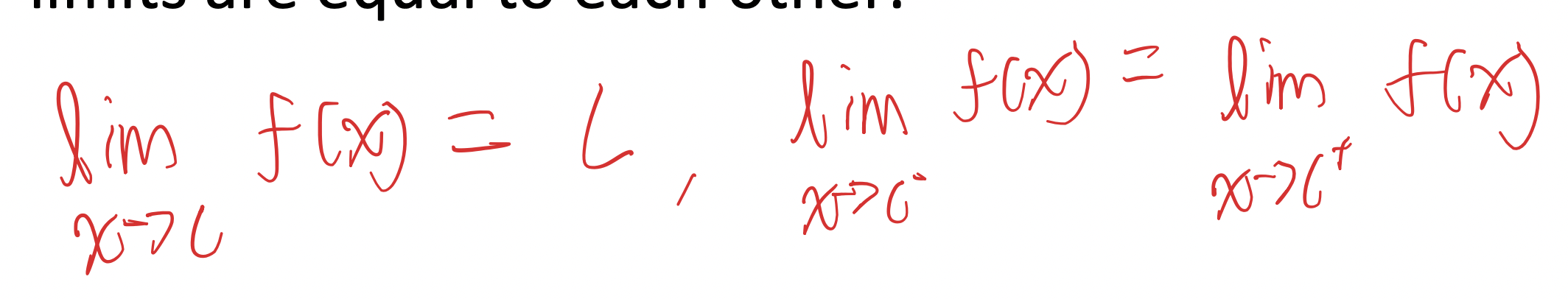
Finding Limits End Behavior

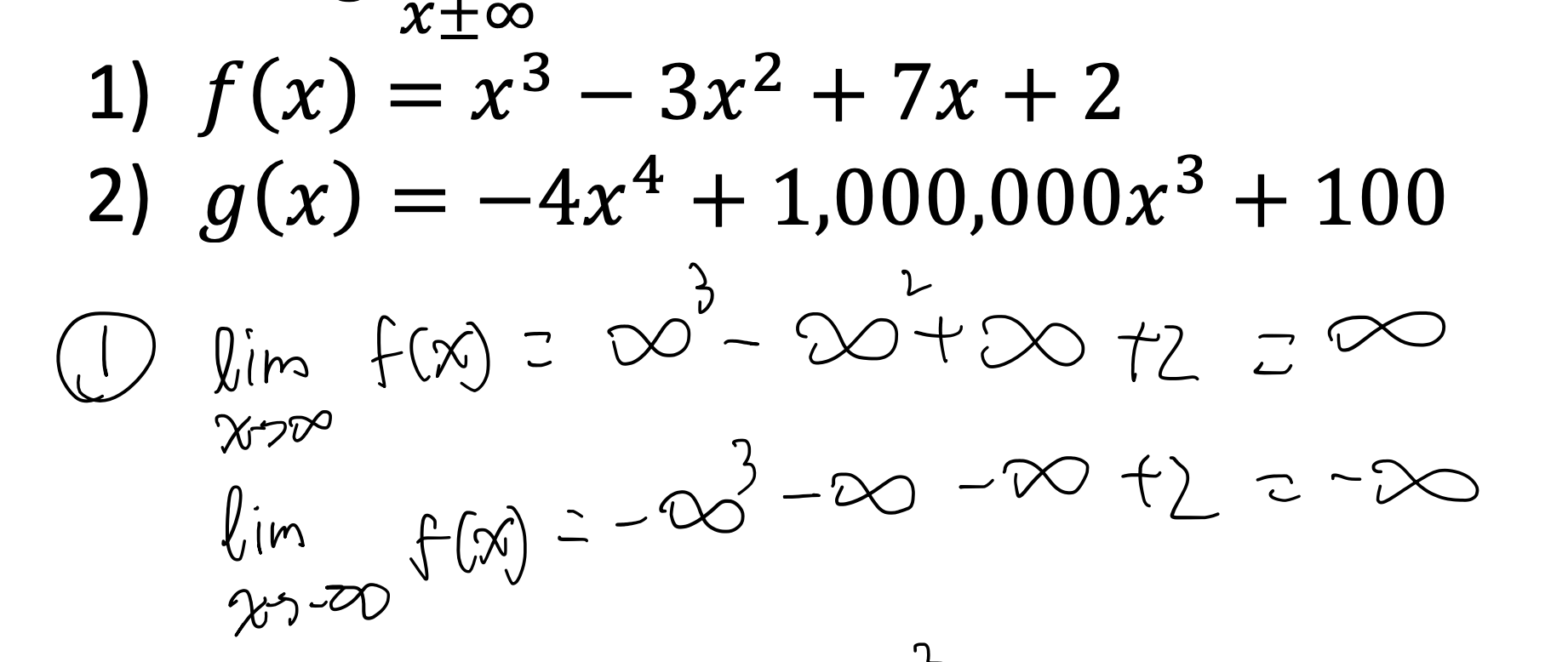
Which value makes vertical asymptotes exist

The value makes denominator (분모) equals to zero.

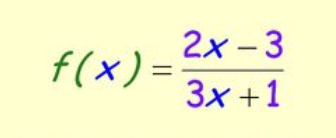
Finding Horizontal Asymptote

y = 2/3

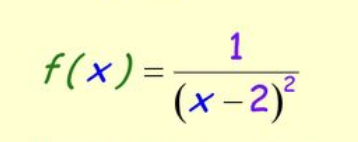
Finding Horizontal Asymptote

y = 0

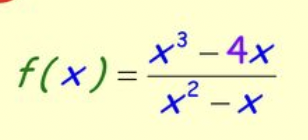
Finding Horizontal Asymptote

No Horizontal Asymptotes

Squeeze Theorem

Squeeze Theorem: If f(x) ≤ g(x) ≤ h(x) for all x in an interval except possibly at x = c, and lim f(x) = lim h(x) = L, then lim g(x) = L.

How to find limits involving infinity?

We need to divide by the biggest power.

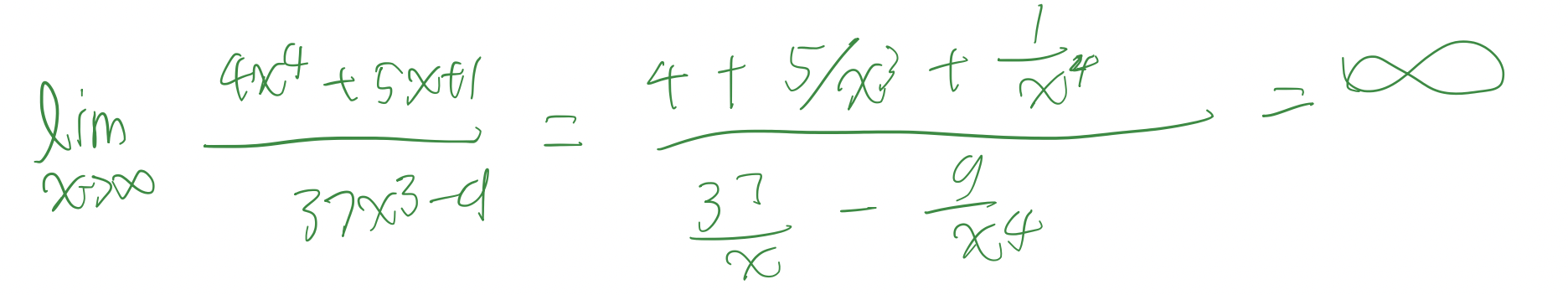
Simplified Version of finding limits involving infinity

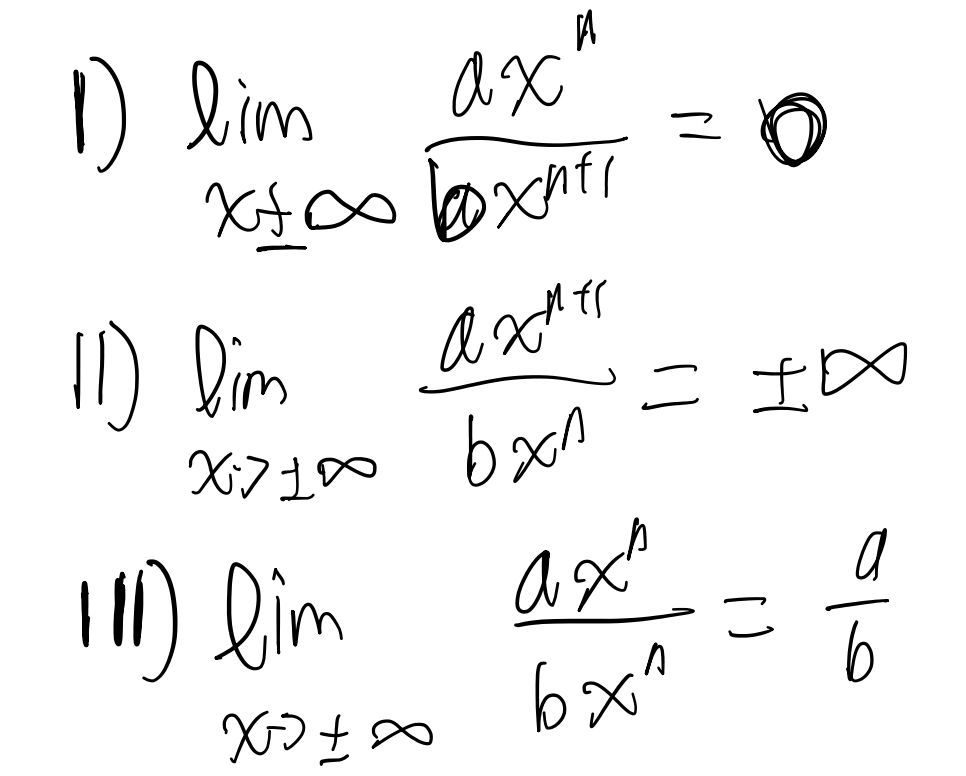
As x approaches 0, limit of sin x/x is

lim (x -> 0) sin(x)/x = 1

As x approaches infinity, limit of sin x/x is

lim (x -> ∞) sin(x)/x = 0

Definition of Continuity

No holes, breaks, or jumps

Three conditions to satisfy that y = f(x) is continuous at x = c.

1) f(c) exists

2) lim (x → c) f(x) exists

3) lim (x → c) f(x) = f(c)

Jump Discontinuity

lim (x→c+) f(x) ≠ lim (x→c-) f(x)

Removable Discontinuity

lim (x→c) f(c) ≠ f(c)

Infinite Discontinuity

When there’s Asymptotes

Theorems on Continuous Functions

1. The Extreme Value Theorem

Extreme Value Theorem: If f is continuous on a closed interval [a, b], then f has both a maximum and minimum value on [a, b].

Theorems on Continuous Functions

1. The Intermediate Value Theorem

If ( f ) is continuous on ([a,b]) and ( k ) is between ( f(a) ) and ( f(b) ), then there exists a ( c ) in ((a,b)) such that ( f(c) = k ).

Example of The Intermediate Value Theorem