Geometry H - Final Exam

Formula for the sum of the interior angles of a polygon?

(n−2)×180

Sum of the exterior angles of any polygon?

360

Each exterior angle of a regular polygon formula?

360/n

Polygon Angle-Sum Theorem

The sum of the measures of the interior angles of an n-gon is (n - 2)180.

Corollary to the Polygon Angle-Sum Theorem

The measure of each interior angle of a regular n-gon is

(n - 2)180/n

Midsegment of a Trapezoid Formula

Midsegment= b1​+b2​/2

polygon

closed figure that is the union of 3 or more sides

diagonal

A line segment connecting one vertex to any other non consecutive vertex.

equilateral

All sides are congruent.

equiangular

All angles are congruent.

regular polygon

Both equilateral and equiangular.

opposite sides

Sides that don’t share a vertex.

consecutive/adjacent sides

Sides that share a common vertex.

opposite vertices

Vertices not connected by a side.

consecutive/adjacent vertices

Vertices that are the endpoints of the same side.

Properties of a Parallelogram?

• Both pair of Opposite sides are parallel.

• Opposite sides are congruent.

• Opposite angles are congruent.

• Consecutive angles are supplementary (add up to 180°).

• Diagonals bisect each other.

“Big 5”

Properties of a rectangle?

• “Big 5”

• Equiangular (90°)

• Diagonals are congruent.

Properties of a rhombus?

• “Big 5”

• Equilateral

• Diagonals are perpendicular.

• Diagonals bisect opposite angles of rhombus.

Properties of a square?

• “Big 5”

• Rectangle with two congruent consecutive sides.

• Diagonals are congruent AND perpendicular.

• Equilateral.

• Rhombus with 4 right angles.

Properties of a Trapezoid?

• Quadrilateral having only TWO sides parallel.

• Legs CANNOT be parallel.

Properties of an Isosceles Trapezoid?

• Base angles are congruent.

• Diagonals are congruent.

• Midsegment is parallel to bases.

• Midsegment = ½ (b1+b2)

Properties of a Right Trapezoid?

• One leg is perpendicular to the bases.

Properties of a Kite?

• Quadrilateral with 2 pairs of consecutive sides congruent AND no opposite sides congruent.

• Diagonals are perpendicular.

How to prove a Paralellogram?

Prove ONE of the following:

• Diagonals bisect each other.

• Two pairs of opposite sides are parallel.

• Both pairs of opposite sides are congruent.

• One pair of opposite sides is parallel and congruent.

How to prove a Rectangle?

Prove the figure is a parallelogram and ONE of the following:

• Figure has one right angle.

• Diagonals are congruent.

How to prove a Rhombus?

Prove the figure is a parallelogram and ONE of the following:

• Diagonals are perpendicular.

• Two adjacent sides are congruent.

How to prove a Square?

• Prove the figure is a rectangle and:

• Two adjacent sides are congruent.

OR

• Prove the figure is a rhombus and:

• It has one right angle.

How to prove a Trapezoid?

• Prove one pair of opposite sides is parallel

AND

• The other pair of opposite sides isn’t parallel.

How to prove an Isosceles Trapezoid?

• Prove the figure is a trapezoid and ONE of the following:

• Legs are congruent.

• Diagonals are congruent.

How to prove a Right Trapezoid?

• Prove the figure is a trapezoid and:

• One leg is perpendicular to a base.

How to prove a Kite?

• Prove two consecutive sides are congruent

AND

• The other opposite sides are not congruent.

How to prove line segments congruent?

• Lengths are = , so the distance formula.

• 

d = √(x2 - x1)² + (y2 - y1)²

How to prove lines parallel?

• They have to be the same slope, so the slope formula.

• m = (y₂ - y₁) / (x₂ - x₁)

How to prove lines perpendicular?

• Slopes are negative reciprocals, so again, its the slope formula.

• m = (y₂ - y₁) / (x₂ - x₁)

How to prove that line segments bisect each other?

• Their midpoints have to be the same, so therefore we have to use the midpoint formula.

• M = (x₁ + x₂)/2, (y₁ + y₂)/2

circle

Set of all pts equidistant from the center.

• Named by its center

• m = 360

diameter

Segment that has both endpts on the circle.

radius

Segment with one endpt. at the center and the other endpt. on the circle.

• All radii are congruent.

congruent circles

Have congruent radii.

central angle

An angle who’s vertex is at the center of the circle.

• m of a central angle = its arc length

arc

Part of the circle.

• named by their endpts.

semicircle

½ of the circle. (180)

minor arc

Smaller than a semicircle.

• named by 2 letters.

major arc

Bigger than a semicircle.

• named by three letters

• usually goes other another arc, hence why its named by three letters.

adjacent arcs

Arcs that have one pt. in common.

Ex: Arc AB and Arc BC.

arc addition postulate

The m of the arc formed by two adjacent arcs is the sum of the m of the 2 arcs.

circumference of a circle

Distance around the circle.

• Formula:

  C = 2πr

  or

• C = πd

arc length

Product of the ratio: (m arc/360)

and (C of the circle.)

Formula:

m arc/360 (πd or 2πr )

chord

Segment whose endpoints are on the circle.

Rule #1

≅ central angles have ≅ arcs.

Rule #2

≅ central angles have ≅ chords.

Rule #3

≅ chords have ≅ arcs.

Rule #4

Chords that are equidistant from the center are ≅.

Rule #5

If a diameter is perpendicular to a chord, then it bisects the chord and its arc.

Rule #6

If the diameter bisects the chord that isn’t a diameter, then it is perpendicular to the chord.

Rule #7

The perpendicular bisector of a chord contains the center of the circle, which means that it is the diameter.

inscribed angle

An angle whose vertex is on the circle and whose sides are chords.

intercepted arc

Arc whose endpts. are sides of the inscribed angles.

inscribed angle theorem

m of an inscribed angle is = to ½ of its intercepted arc.

• Angle is ½ the arc.

tangent

A line that intercects the circle at only one point on the outside of the circle.

common tangent

Line that is tangent to two circles.

secant

A line that intersects the circle at 2 points.

tangent segments

Segment of a tangent line.

Two _____ drawn from an external point that are congruent.

angles formed by tangent and chord

The angle formed by a tangent and a chord is ½ its arc.

angles formed by two chords

The angle formed by 2 chords intersecting inside a circle is ½ the sum of the intercepted arcs.

angles formed by two secants, a tangent and secant, or two tangents

The angle formed by wo secants, a tangent and secant, or two tangents intersecting inside a circle is ½ the difference of the intercepted arcs.

measures of chords

If two chords intersect in a circle, the product of the segments of one chord = the product of the segments of the other chord.

measures of secants

If two secants intersect outside a circle, the product of the whole secant and its external segment = product of other whole secant and its external segment.

measures of tangent and secant

If a tangent and secant are drawn to a circle from an external point, then the square of a tangent segment = product of whole secant and external fragment.

equation of a circle

If the center of the circle is at the origin -

x² + y² = r².

equation of a circle

If the center of the circle is not at the origin -

(x – h)²+ (y – k)² = r²

(h, k) = the coordinates of the center of the circle

r = the radius of the circle

transformation

Change in positions, shape, size, or figure

pre-image

Original image

image

• Resulting image;

  • Figure after transformation

rigid motion

• A transformation that preserves distance and angle measure.

  • Pre image and image have the same length between points and same angle measures.

  • Transformations map every pt. of a figure onto its image.

translation

• A transformation that maps all points of a figure the same distance in the same direction.

  • Figure “slides”

  • Rigid motion

translation formula

T (x, y) → (x + a, y + b)

reflection

• A transformation in which a figure is reflected over a given line.

  • Rigid motion

  • Each pre-image pt corresponds to only one image pt.

reflection formula

x-axis : (x, y) → (x, -y) (y value negates)

y-axis: (x, y) → (-x, y) (x value negates)

rotation

• A transformation in which a figure is turned around a point.

  • symbol: r

    • Called the point of rotation or center of rotation.

    • Rotates counter clockwise around origin

    • Rotations that are clockwise are negative.

    • Rigid motion

What’s the rule for a + 90° rotation?

• Switch, negate the first.

What’s the rule for a 180° rotation?

• Don’t switch, negate both.

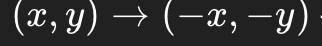
What’s the rule for a +270° rotation?

Same as -90, Switch and negate second.

What’s the equivalent of a -90° rotation?

• Same as 270, Switch and negate second.

dilation

• makes the figure bigger or smaller.

  • Distance not preserved, but angle measure is.

  • Formula: Dₖ (x,y) → (kx, ky) always multiply

space figures

3 dimensional figure.

polyhedron

A space figure whose surfaces are polygons.

face

Polygon.

edge

Line segment formed by the intersection of two faces.

vertex

Point where three or more edges meet.

euler’s formula

Sum of the # of faces (F) and vertices (V) of s polyhedron id two more than the # of its edges (E).

F+V = E+2

prism

Polyhedron of which two faces (called bases) are congruent parallel polygons and the other faces are called lateral faces (sides)

• Lateral faces are ALWAYS rectangles.

lateral area

Sum of the areas of lateral faces (LA).

surface area

LA + area of the bases.

• Called SA.

volume

Bh

• B = area of the base.

cylinders

• Solid that has two congruent parallel bases that are circles.

altitude of cylinder

• Perpendicular segment that joins the bases.

• Also called height.

lateral surface

Picture “unrolling” label of a can.

la of cylinder

LA = 2πrh

r = radius

h = height

sa of cylinder

SA=LA + 2(πr²)