Convergence and Divergence Tests for Series

Flashcards summarizing key convergence and divergence tests for series.

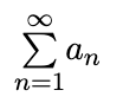
Test for Divergence

Diverges if limn→∞ an ≠ 0 or limn→∞ an does not exist; inconclusive if limn→∞ an = 0.

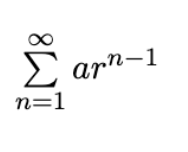
Geometric Series

Converges if |r| < 1; diverges if |r| ≥ 1; sum is Σ∞ n=1 arn−1 = a / (1 - r).

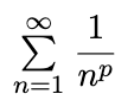
p-series

Converges if p > 1; diverges if p ≤ 1.

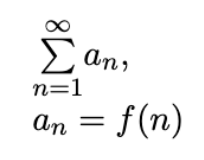
Integral Test

Converges if ∫∞1 f(x)dx converges; diverges if ∫∞1 f(x)dx diverges, where f derived from an is continuous, positive, and decreasing.

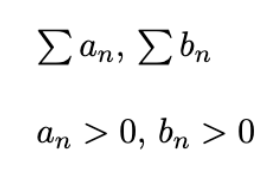
Comparison Test

If Σbn converges and an ≤ bn for all n ≥ 1, then Σan converges; if Σbn diverges and an ≥ bn for all n ≥ 1, then Σan diverges.

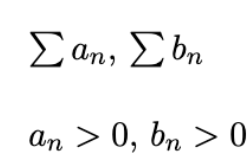
Limit Comparison Test

If limn→∞ an/bn = c > 0, then either both series converge or both diverge.

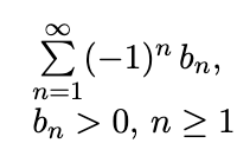
Alternating Series

Converges if bn+1 ≤ bn for all n ≥ 1 and limn→∞ bn = 0.

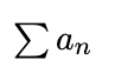
Absolutely Convergence

If Σ|an| converges, then Σan converges.

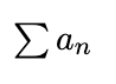
Conditionally Convergence

If Σan converges but Σ|an| diverges.

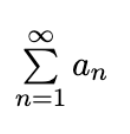
Ratio Test

If limn→∞ |an+1/an| = L, then the series is absolutely convergent if L < 1, divergent if L > 1 or ∞, inconclusive if L = 1.

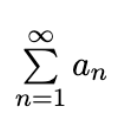
Root Test

If limn→∞ n√|an| = L, then the series is absolutely convergent if L < 1, divergent if L > 1 or ∞, inconclusive if L = 1.