How to Use Squeeze Theorem (and when)

The Squeeze Theorem is a versatile and essential tool in calculus, especially when evaluating limits that are not straightforward. Here's a refined breakdown to make the explanation easier to follow:

Squeeze Theorem Statement

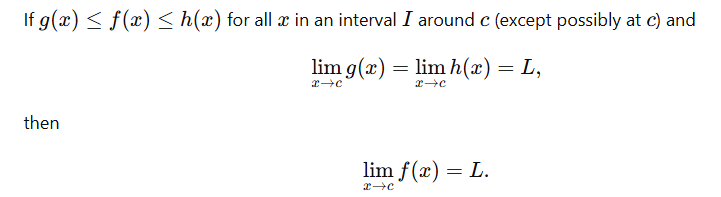
When to Use the Squeeze Theorem

1. Complex or Oscillatory Behavior:
   Use the theorem for functions with challenging behavior, such as oscillations, that are hard to evaluate directly.

2. Behavior Near a Point:
   Applicable when f(x)'s behavior near c is tightly bounded by simpler functions g(x) and h(x).

3. Trigonometric, Exponential, or Absolute Value Terms:
   Works well for functions involving absolute values or products of oscillatory terms and polynomials.

Steps to Apply the Squeeze Theorem

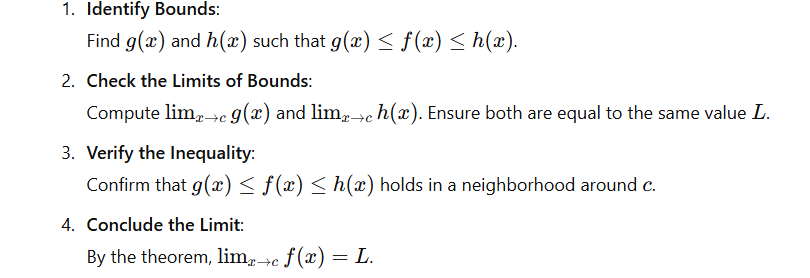
Common Pitfalls

1. Failure to Verify Bounds:
   Always confirm g(x) ≤f(x) ≤h(x) near c.

2. Unequal Bounding Limits:
   If lim_x→c​ g(x) ≠ lim_x→c​h(x), the theorem cannot be applied.

3. Inequality Must Hold in a Neighborhood:
   g(x) ≤ f(x) ≤ h(x) must be valid in an interval around c, not just at isolated points.

Summary

The Squeeze Theorem is ideal for limits of functions bounded between two simpler functions with the same limit. It's particularly useful for oscillatory functions or when direct evaluation is impractical. By ensuring bounds and their limits are correctly identified and verified, you can confidently conclude the desired limit.