The derivative tells us the slope of the line tangent to the graph- which tells us the slope of the line at a particular point
This means that they can tell us the change of a unit over time. This will make sense with straight line motion.

We know that position is measured in meters
We know that velocity is measured in meters per second (m/s)
- Therefore we can derive position to get the rate of change- ie. meters per second!
We know that acceleration is measured in meters per second squared (m/s^2)
- So we can derive velocity to get the rate of change- ie. meters per second per second!
- You can also take the second derivative of position to get acceleration

Position:	x(t) (sometimes wrote as s(t))	Meters
Velocity:	x’(t) or v(t)	Meters/Second
Acceleration:	x”(t) or v’(t) or a(t)	Meters/Second^2

Particles will speed up when the sign of velocity and acceleration match
The must both be negative or positive
For example, if a particle moves along a straight line with velocity function v(t) = 3t^2 - 4t + 2. Find the acceleration of the particle at time t=2?
- Solution: The acceleration of the particle is the derivative of its velocity function. Thus, we take the derivative of v(t) with respect to t
- a(t) = d/dt v(t) = 6t - 4
- To find the acceleration at t=2, we substitute t=2 into the expression for a(t):
- a(2) = 6(2) - 4 = 8

The derivative can also tell us the change of something other than motion

For example, let’s say the volume of water in a pool is equal to V(t) = 8t^2 -32t +4
Where V is the volume in gallons and t is the time in hours
If we want to find the rate that the volume of water is increasing we take the derivative
- dV/dt = 16t - 32 gallons per hour
- At t=2 the volume isn’t changing (equation equals 0)
- Therefore it is increasing for all values >0
Another example would be where temperature of a cup of coffee is given by the function x(t) = 70 + 50e^(-0.1t), where t is the time in minutes since the coffee was poured. And we need to find the rate of change of the temperature with respect to time at t=5 minutes.
- d/dt of x(t) = -5e^(-0.1t)
- Evaluating this derivative at t=5 minutes, we get:
- x’(5) = -5e^(-0.1(5)) ≈ -2.27

We just saw how the derivative can tell us the change of something but we can also have problems where the change of one thing is related to another- Related Rates!
Let’s say that a pool of water is expanding at 16π square inches per second and we need to find the rate of the radius expanding when the radius is 4 inches
We know that we can find the radius using A = πr^2
Now let’s relate our rates!
- dA/dt = 2πr(dr/dt)
- Notice how we had to follow r with dr/dt, this is because the change in R doesn’t match the change in A (implicit differentiation)
- Now we have the change of the area (dA/dt) and the change of the radius (dr/dt)
- Now we can plug in and solve!
- 16π = 2π(4)dr/dt
- dr/dt = 2
- The radius is changing at a rate of 2 inches per second
Let’s say a spherical balloon is being inflated at a rate of 10 cubic inches per second. How fast is the radius of the balloon increasing when the radius is 4 inches?
We know that the volume of a sphere is given by the formula V = (4/3)πr^3.
- Differentiating both sides with respect to time t, we get:
- dV/dt = 4πr^2 (dr/dt)
- We are given that dV/dt = 10 cubic inches per second and r = 4 inches. Substituting these values, we get:
- 10 = 4π(4^2)(dr/dt)
- Simplifying, we get:
- dr/dt = 10/(16π)
Therefore, the radius of the balloon is increasing at a rate of 10/(16π) inches per second when the radius is 4 inches.
To solve related rates problems in calculus, follow these steps:

Remember to always include units in your final answer and to check that your answer makes sense in the context of the problem.

Differentials are very small quantities that correspond to a change in a number. We use Δx to denote a differential.
- They can approximate the value of a function!
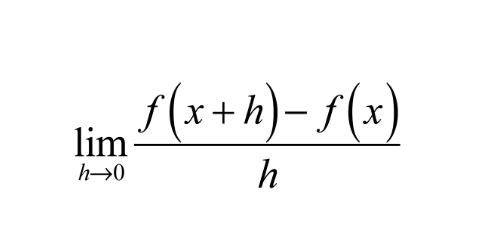
Remember the limit definition of a derivative?
We just have to replace h with Δx and remove the limit!
- We get that f(x + Δx) ≈ f(x) + f’(x)Δx
- This is no longer equal to the derivative, but an approximation of it
- In simple terms “the value of a function (at x plus a little bit) is equal to the value of the function (at x) plus the product of the derivative of the function (at x) plus a little bit”
Let’s say we needed a differential to approximate (3.98)^4
- We have to let f(x) = x^4, x= 4, and Δx = -0.02
- Now we have to find f’(x) which is 4x^3
- Now plug into f(x + Δx) ≈ f(x) + f’(x)Δx
- (x + Δx)^4 = x^4 + 4x^3Δx
- When we plug in x= 4 and Δx= -0.02 we get 250.88
- You can check this using your calculator!

If a limit gives you 0/0 or ∞/∞, then it is called “indeterminate” and you can use
L’Hospital’s Rule to interpret it!
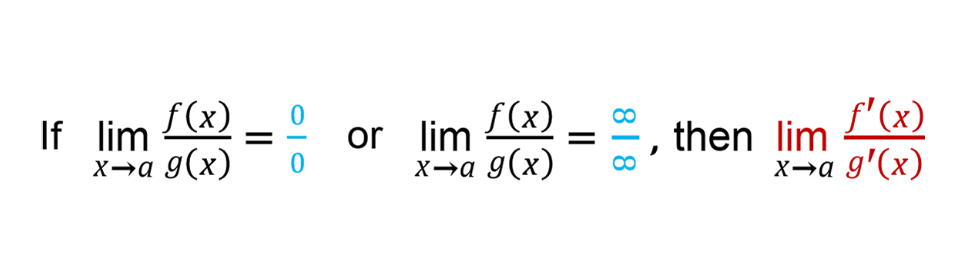
L’Hospital’s Rule says that we can take the derivative of the numerator and denominator and try again
Let’s say we have the limit of 5x^3 -4x^2 +1/7x^3 +2x - 6 as it approaches infinity
- This equals ∞/∞ so we can take the derivative of the top and bottom
- Then we get 15x^2 -8x/21x^2 +2
- This is still ∞/∞ so we take the derivative again
- Then we get 30x -8/42x which is still ∞/∞
- We take the derivative to get 30/42 or 5/7 which is our answer!