Nth Term Test for Divergence
The Nth Term Test for Divergence is an essential tool for identifying whether an infinite series diverges. Here's a concise guide based on your detailed content:
Purpose:
To check if an infinite series diverges by examining the behavior of its general term an as n→∞.
Test Statement:

Why This Test Works:
For a series to converge, the general term an must approach 0 as n→∞.
If an does not approach 0, the series cannot converge, because the sum of infinitely large terms cannot settle to a finite value.
Steps to Apply:
Identify the General Term: Write the formula for an.
Compute the Limit: Use algebraic techniques or calculus to evaluate limn→∞an.
Interpret the Result
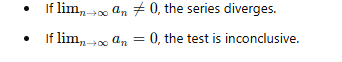
Key Limitations:
Divergence Only: This test cannot prove convergence. A limit of zero is necessary for convergence but not sufficient.
Further Testing Required: When limn→∞an= 0, use additional tests (e.g., Comparison Test, Ratio Test, Integral Test).
Examples:
Example 1: Divergence
Series:
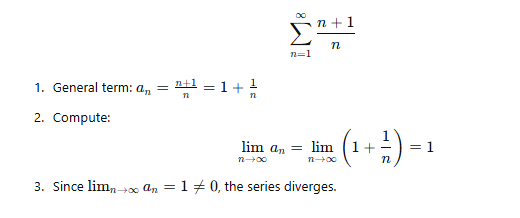
Example 2: Inconclusive
Series:

Common Misunderstandings:

Conclusion:
The Nth Term Test is a quick first step in determining whether an infinite series diverges. It simplifies analysis but must be supplemented with other tests for a complete understanding of series behavior.
